Слайд 2Дәріс жоспары:
санау жүйесі туралы түсінік;
позициялық, позициялық емес санау жүйелері;
әртүрлі
санау жүйелірі туралы түсінік;
негіздері q=2, 8 ,16 с. ж.арасындағы байланыс;
санау
жүйелеріндегі түрлендірулер;
ауыстырудың кестелік әдісі;
әртүрлі санау жүйелеріндегі сандардың сәйкестігі;
екілік санау жүйесіндегі арифметикалық амалдардың орындалуы.
Слайд 3Санау жүйесі - сандарды арнайы берілген белгілер (цифр) арқылы жазудың
әдістері мен ережелері.
Кез келген санау жүйесі белгілі бір таңбалардың жиынтығын
қолданады.
Мұндай таңбалар жиынтығын – санау жүйесінің алфавиті деп атайды.
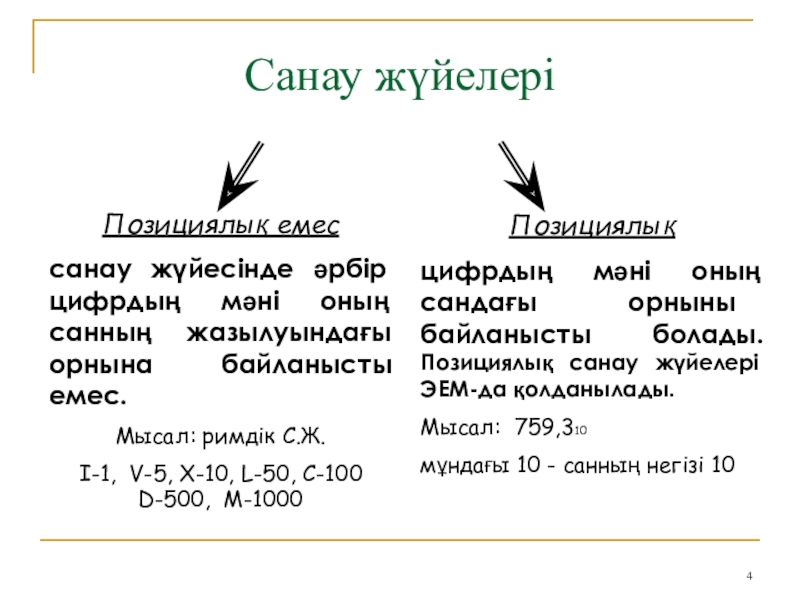
Слайд 4Санау жүйелері
Позициялық емес
санау жүйесінде әрбір цифрдың мәні оның санның
жазылуындағы орнына байланысты емес.
Мысал: римдік С.Ж.
I-1, V-5, X-10, L-50, C-100 D-500, M-1000
Позициялық
цифрдың мәні оның сандағы орныны байланысты болады. Позициялық санау жүйелері ЭЕМ-да қолданылады.
Мысал: 759,310
мұндағы 10 - санның негізі 10
Слайд 5Позициялық емес СЖ құрылымы қарапайым
Римдік санау жүйесін қарастыратын болсақ, I,X,V,
L(50), C(100), D(500), M(1000) және т.б. белгілер жиынтығынан тұрады.
Мұнда
бірнеше сан негізгі (I,X,V),
ал қалғандары осы негізгі сандарға қосу (VI, VII)
немесе алу (IV, IX) арқылы алынады.
Мысал: CCXXXII саны екі жүздіктен, үш ондықтан және екі бірліктен тұрады.
Слайд 6Римдік санау жүйесінде сандағы цифрлар солдан оңға қарай кемуі бойынша
жазылса, онда олардың мәндері қосылады.
Мысал :
XXVII 10+10+5+1+1+=27
MMMD
1000+1000+1000+500=3500
MDCCLXVII
1000+500+100+100+50+10+5+1+1=1767
Слайд 7кафедра информатики У-Ка, 2007
Ал санның жазылуында цифрдың мәні өзінің
оң жағындағы цифрдан кем болса, онда ол сан оң жақтағы
саннан азайтылады.
IV 5-1=4
XIX 10+(10-1)=19
MCMXCIV
1000 + (-100+1000) + (-10+100) + (-1+5)=1994.
MCMXCVIII
1000+ (-100+1000) +(-10+100) + 5+1+1+1=1998.
Слайд 8кафедра информатики У-Ка, 2007
Позициялық санау жүйесі үшін.
мұндағы
x – санау жүйесінің негізі
ai – сан
цифрлары
i – позиция (разряд) номері (0 –ден басталады)
төмендегі өрнек орындалады :
+ a0*x0
+ a1*x1
+ a3*x3
+ a2*x2
+ a4*x4
…
…a4a3a2a1a0 =
Слайд 9
Позициялық санау жүйесінде цифрдың мәні оның сандағы орныны (позициясына) байланысты
болады.
Мысал, 555 санындағы бірінші цифра мәні-5 бірлік, екінші цифрдфң
мәні – 5 ондық және үшінші цифрдфң мәні 5 жүздік.
52515010 =5*102 + 5 * 101 + 5 * 100 Мұнда санау жүйесінің негізі – 10.
Кез келген позициялық санау жүйесінде негіз ұғымы қалыптасқан. Берілген санау жүйесіндегі санды өрнектеуге қолданылатын белгілер мен цифрлар саны сол санау жүйесінің негізі (базис) деп есептеледі.
Мысал: екілік санау жүйесінде негіз – 2, ондық
санау жүйесінде негіз – 10.
Слайд 10Позициялық санау жүйесінде сан коэффициенттерінің санау жүйесінің негіз дәрежесіне
көбейтінділерінің қосындылары түрінде беріле алады.
Мысалдар:
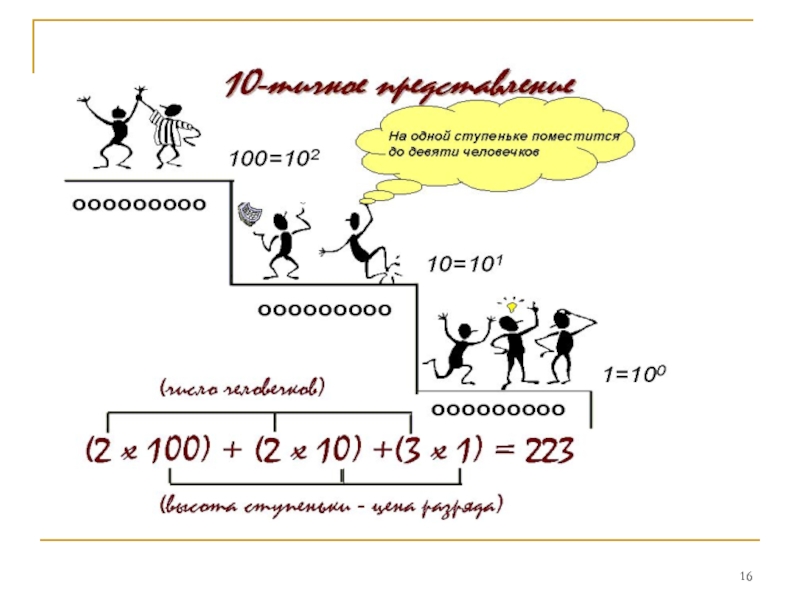
Слайд 11Ондық санау жүйесі жаңа эраның VI ғ. шамасында Индияда пайда
болған деп есептеледі. Санау жүйесінің негізі -10.
Ондық санау жүйесінде санда
жазу үшін он цифр қолданылады – 0,1,2,3,....9, бірақ мағананы тек қана цифр ғана емес оның тұрған орны да береді.
Ондық санау жүйесі
Слайд 12Ондық санау жүйесі
мысалы, 1062 – ондық санау жүйесінің саны
Слайд 13Бөлшек бөліктегі әрбір цифр үшін негіздеуші дәреже теріс, бөлшек бөліктің
үлкен цифры үшін ол (-1), келесі цифры үшін (-2) және
т.с.с.
Мысал, 1253, 785 ондық саны мынадай қосындымен беріледі:
және керісінше:
Егер сан бөлшек болса, онда ол қосынды түрінде оңай жазылады.
р е ж е с і
Бұл жағдайда берілген
бөлшек санды санның бөлшек бөлігін және шыққан көбейтінділерді р негізіне тізбектеп көбейту қажет. Шыққан көбейтіндінің бүтін бөліктері берілген санның р негізді жүйедегі цифрларын береді.
Көбейтуді ізденімді р негізді сандар салмағы берілген q негізді санның кіші разряды салмағынан кем аз разрядтарға дейін жүргізу керек. Жалпы жағдайда бұл үрдіс шексіз болуы мүмкін. Сондықтан алынған код көп жағдайда жуық сан болады. Тәжірибеде осы операциялар үтірден кейін берілген цифр саны алынғанша орындалады.
Слайд 15
Оң ондық бөлшекті екілік санау жүйесіне ауыстыру үшін бөлшекті 2-ге
көбейту қажает. Көбейтіндінің бүтін бөлігі екілік бөлшектің үтірден кейінгі бірінші
цифры ретінді алынады. Екілік бөлшектің келесі цифры ретінде осы көбейтіндіні алады, ал көбейтіндінің бөлшек бөлігін қайтадан 2-ге көбейтеді және т.с.с.
Мысал 6. Ондық бөлшекті А = 0,5625 екілік санау жүйесіне ауыстыру (q2=2)
0, 5625*2
1 1250*2
0 2500*2
0 5000*2
1 0000 Жауабы: 0,5625 10 – 0,10010 2
Мысал 7 : 0,375*2=0,75
0,75*2=1,5
0,5*2=1
0,37510=0,0112
Слайд 17Екілік (бинарлық) санау жүйесі.
Компьютерде негізі екіге тең екілік санау жүйесі
қолданылады. Бұл жүйеде кез келген сан бар жоғы екі сан
0 мен 1 арқылы өрнектеледі.
Мысалы, &101
& - амперсант деп аталады, санның екілік жүйеде жазылғанын білдіреді.
Екілік санның әрбір рязрядын (цифрын) бит деп атайды.
Ондық сандар сияқты екілік санды да қосынды түрінде жазуға болады.
Мысалы, 110101 екілік сан үшін қосынды мына түрде болады:
Слайд 18Екілік санау жүйесі
Мысалы, &1010 – екілік санау жүйесіндегі сан
= 10
Слайд 19Екілік санау жүйесінде әрбір цифрдың мәні тұрған орнынан үлкен келесі
разрядқа көшкенде екі есе өседі.
Бір битпен 0 немесе 1
деген екі ұғым өрнектеледі. Ал егер бит санын екіге өсірсе, онда әртүрлі төрт ұғым өрнектеуге болады:
00 01 10 11
Үш бит арқылы сегіз ұғым өрнектеледі:
000 001 010 011 100 101 110 111
Екілік кодтау жүйесінде разряд санын бірге өсіру арқылы, біз нәтижесінің санын екі есе өсіреміз. Оның ортақ формуласының түрі:
N= 2 m.
мұндағы N – кодталатын еркін мәндердің саны;
m – берілген жүйеде қабылданған екілік кодтаудың разряды.
Слайд 20Екілік санау жүйесі
&101 =
5
&110 =
&111
=
6
7
= 8
&1000
= 9
&1001
“Дөңгелек” сандар
&1 =
1
&10 = 2
&100 = 4
&1000 = 8
&10000 = 16
&100000 = 32
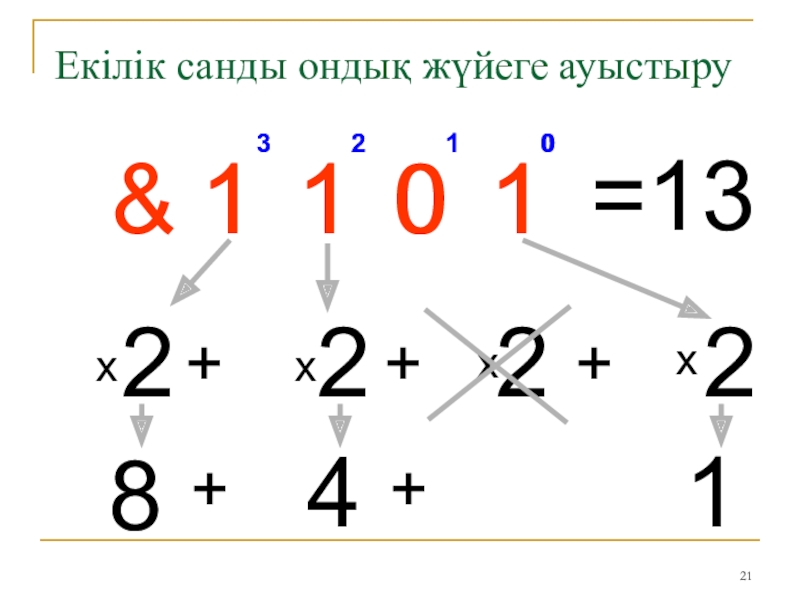
Слайд 21x
Екілік санды ондық жүйеге ауыстыру
0
1
2
3
1
0
1
1
&
1
2
0
+
0
2
1
1
+
2
2
+
1
2
3
1
+
4
+
8
=13
x
x
x
Слайд 22
Екілік санау жүйесін ЭЕМ жасаушы инженер-конструкторлар ойлап шығарды деген жаңсақ
пікір. Екілік санау жүйесін компьютерлердің пайда болуынан көп уақыт бұрын
(XVII-XIX ғасырлар) математиктер мен философтар ойлап шығарған.
Атақты неміс ғалымы Лейбниц былай деп жазған: «Екілік сандармен есептеу – ғылым үшін негізгі болып табылады және жаңа ғылыми жаңалықтар ашуға жол береді... Сандарды 0 мен 1 сияқты қарапайым түпнегізге келтіргенде, барлық жерде таңғажайып тәртіп пайда болады». Кейіннен қолданыс таппаған екілік жүйе ұмытылды, тек қана 1936-1938 жылдары электронды схемаларды құрастыру кезінде американдық инженер-математик Клод Шеннон оған керемет қолданыс тапты.
Екілік санау жүйесінің негізгі жағымды жағы - аппараттық қолданысқа барынша ыңғайлы арифметика амалдарының орындалу қарапайымдылығы. Екілік санау жүйесі компьютерге ыңғайлы болғанымен, адам үшін жазылуының ұзындығы мен еске сақтауғақиындығынан қолайсыз.
Слайд 231950-70 жылдарда бағдарламалауда кең қолданылған.
Сегіздік санау жүйесі санды сегіз цифрдың
(0,1,....7.) көмегімен көрсетеді (негізі – 8).
Мысал:
5368= 5*82 + 3*82 +
6*80 = 5*64 + 24 + 6 = 35010
53610 = 3508
8 саны 2 санының дәрежесі болатындықтан сегіздік санау жүйесін екілік сандарды жазудың ықшам нұсқасы ретінде қарастыруға болады.
Сегіздік санау жүйесі
Слайд 24
Он екілік санау жүйесі ертеректе кең қолданыста болған. Оның пайда
болу тарихы да саусақпен санауға байланысты. Мұнда бас бармақты және
қалған төрт саусақтың фалангаларын санаған: олардың саны -12.
Он екілік санау жүйесінің элементтері Англияда әлі күнге дейін сақталып қалған (1 фут 12дюйм), 1 шиллинг 12пенс). Бұл санау жүйесімен біз тұрмыста жиі кездесеміз: асханалық және шай сервистерінің саны 12, т.с.с.
Он екілік санау жүйесі
Слайд 25Он алтылық позициялық санау жүйесінде санды жазу үшін ондық санау
жүйесінің цифрлары 0,1,.....9, және жетпейтін алты цифрды белгілеу үшін мәні
ондық 10, 11, 12, 13, 14, 15 цифрларына сәйкес болатын латын алфавитінің алғашқы үлкен әріптері A, B, C, D, E, F қолданылады.
Мысал, 3Е5А1 санын негіз қосындысы түрінде жазсақ, мынаны аламыз:
Мысал: ондық жүйедегі 891 санын 16-лық санау жүйесіне көшіру үшін:
891 : 16 =55 қалдық 11 (16-лық санау жүйесінде 11=В)
55 : 16 = 3 қалдық 7
3 : 16 = 0 қалдық 3 Жауабы: 37В16
Он алтылық санау жүйесі
Слайд 26Вавилондық санау жүйесі
Алғашқа позициялық санау жүйесі ертедегі Вавилонда (б.ғ. д.
2000 ж.) құрылған, ол негізі 60-қа тең алпыстық санау жүйесі
болған. Айта кететіні, уақытты біз осы кезге дейін негізі 60-қа тең өлшеммен есептейміз.Сол сияқты шеңберді 360 бөлікке бөлеміз.
алпыстық санау жүйесі
Слайд 27
Екілік арифметика ережесі
1. Қосу :
2. Азайту :
1+1=10 1-1=0
1+0=1 1-0=1
0+1=1 0-1=1
0+0=0 0-0=0
Слайд 28Негіздері q=2, q=8 және q=16 болатын санау жүйелері арасындағы байланыс
екі теорема арқылы анықталады.
Слайд 29Теорема 1. Негізі q=2n болатын санау жүйесінде бүтін екілік санды
жазу үшін, берілген екілік санды оңнан солға қарай (ең кіші
разрядынан үлкеніне қарай) әрбірінде n цифр болатындай топтарға (грани) бөлу керек. Одан кейін осы топтың әрқайсысын n разрядты екілік сан ретінде қабылдап оны негізі q=2n болатын санау жүйесінің цифры етіп жазу.
Мысал: 101100001000110010 екілік санын оған сәйкес келетін 8-дік санау жүйесінің (басқаша айтқанда негізі q = 23 ) санымен ауыстыру.
101 100 001 000 110 010
5 4 1 0 6 2
Сонымен, екілік 101 100 001 000 110 010 саны
сегіздік санау жүйесінде 541 062
Слайд 30Теорема 2.
Негізі q=2n болатын санау жүйесінде жазылған бүтін санды
оған сәйкес екілік санау жүйесіндегі санмен ауыстыру үшін, берілген санның
әрбір цифырын n разрядты екілік санмен ауыстыру жеткілікті.
Мысал: 3 5 6 7 сегздік санын өзіне сәйкес екілік санмен ауыстыр
3 5 6 7
011 101 110 111 3 5 6 7 - 011 101 110 111
Сонымен, екілік санды оған сәйкес сегіздік санға ауыстыруды ешқандай есептеулерсіз, механикалық түрде жүзеге асыруға болады.
0 1 2 3 4 5 6 7
000 001 010 011 100 101 110 111
Слайд 31Сандардың сәйкестік кестесі
255 = &11111111 =
#ff
Слайд 32Сандарды екілік жүйеден сегіздік, он алтылық санау жүйелеріне ауыстыру.
Бүтін екілік
санды сегіздік (он алтылық) санау жүйесіне көшіру үшін, оны оңнан
солға қарай үш үштен (төрт төрттен) топтап, жетпеген орындары болса нольмен толтырып, сонан соң әрбір топтың орнына оның сегіздік (он алтылық) эквивалентін қою қажет.
Мысал: 001 101 101 011 екілік саны =1553 сегіздік санына
0011 0110 1011 екілік саны =36B он алтылық санына
Екілік жүйедегі бөлшек санды немесе санның бөлшек бөлігін сегіздік (он алтылық) жүйеге көшіру үшін санды үтірден кейін оң жақ шеткі нуктеге дейін триадаларға (тетрадаларға) бөлу керек. Содан кейін әрбір триадаға (тетрадаға) сәйкес сегіздік (он алтылық) санды жазу керек.
Мысал: 0,011 101 100 екілік саны =0,354 сегіздік санына
0,0111 0110 екілік саны =0,76 он алтылық санына
Слайд 33Екілік цифрлардың үштік топтарын – триада деп атайды.
Мысал 13.
Екілік
1100101101 санын үштен топқа бөлгенде, 001 100
101 101 сияқты жазуға болады және әрбір топты сегіздік цифрдың біреуімен ауыстырып жазғанда, 1455 сегіздік санын аламыз.
Слайд 34Санды екілік санау жүйесінен сегіздік не он алтылық жүйеге ауыстыру
үшін, кестені пайдаланамыз:
Мысал, санды екілік жүйеден сегіздік жүеге ауыстырайық
11111000100
Оңнан солға
қарай үш үштен бөлеміз
Бір ноль жетіспегендіктен, бір ноль қосып жазамыз .
(егер екеу жетпесе екі ноль қосқан болар едік т.с.с..)
0
Енді кестенің көмегімен жауабын жазамыз.
Мысалы, екінші бағандағы 011 саны, біріншідегі
3 санына сәйкес (эквивалентті)
сол сияқты 111 = 7; 000 = 0; 100 = 4
жауабы:
(11111000100)2 = (3704)8
Слайд 35Санау жүйелеріндегі түрлендірулер.
Компьютер екілік кодтармен жұмыс жасайды. Ал пайдаланушы ондық,
он алтылық кодтармен жұмыс жасайды. Сондықтан қандай бір q негізді
санау жүйесіндегі А санын р негізді санау жүйесіндегі А санына түрлендіру және кері түрлендірулер қажет болады.
Мұндай түрлендірулер негізгі екі әдіспен жүзеге асады:
ауыстыру ережелері арқылы;
бөлу, көбейту ережелері арқылы.
Ауыстыру ережесі бірінші формуланың көмегімен жүзеге асырылады және көбінесе, ондық емес санау жүйесінен ондық санау жүйесіне көшу үшін қолданылады. Ауыстыру ережесі санның жаңа жүйедегі кодымен арифметикалық операциялар жүргізуді ескертеді.
Бөлу, көбейту ережелері.
Көбінесе ондық санау жүйесінен басқа санау жүйесіне көшу үшін қолданылады. Бұл ереже санның алғашқы q негізді жүйедегі кодымен арифметикалық операциялар жүргізуді ескертеді. Бөлу ережесі бүтін санды түрлендіру үшін, көбейту дұрыс бөлшек санды түрлендіру үшін қолданылады.
Слайд 36Б ө л у
е р е ж е
с і.
Ол үшін берілген q негізді санды және шығатын бөлінділерді
р негізіне тізбектеп бөлу қажет. Бөлуді бөлінді р негізінен кіші болғанша жалғастыру қажет. Санның жаңа р негізді жүйедегі орнын алу үшін ең соңғы бөліндіден бастап, бөлуге кері бағытта қалдықтарды тізбектеп жазу қажет.
Слайд 37Ондық жүйедегі бүтін санды немесе санның бүтін бөлігін екілік жүйеге
көшіру үшін, бөлінді 0-ге немесе 1-ге тең болғанша бөлу керек.
Ең соңғы бөліндіден бастап, қалдықтарды тізбектеп кері бағытта жазғанда шыққан сан – берілген санның екілік жүйедегі коды болып табылады.
Мысал: 25/2=12 (қалдық 1)
12/2=6 (қалдық 0)
6/2=3 (қалдық 0)
3/2=1 (қалдық 1)
1/2=0 (қалдық 1)
2510=110012
Слайд 38
Ондық 25 санын екілік санау жүйесіне көшіру
25 = &11001
Тексеру:
1* 24
+ 1*23+ 0*22 + 0*21 + 1*20 =
1*16 + 1*8
+ 0*4 + 0*2 + 1*1 =
16 + 8 + 0 + 0 + 1 = 25
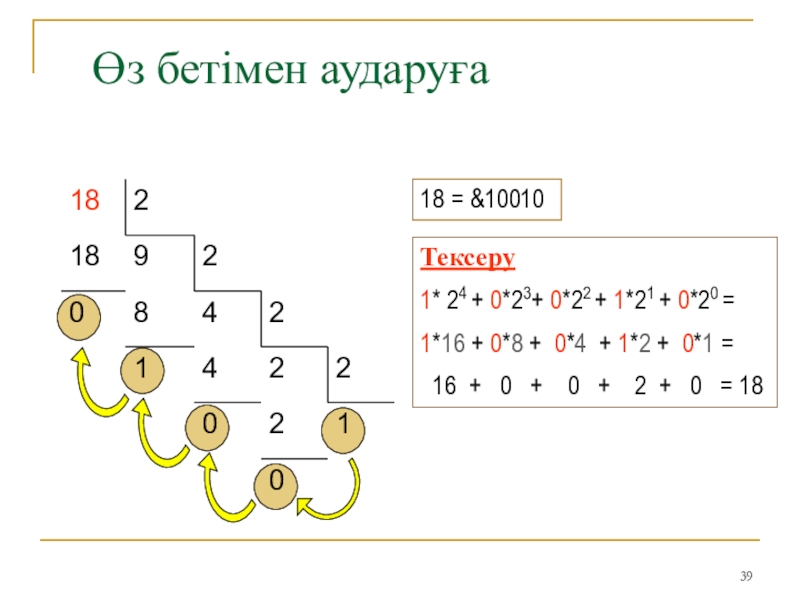
Слайд 39
Өз бетімен аударуға
18 = &10010
Тексеру
1* 24 + 0*23+ 0*22 +
1*21 + 0*20 =
1*16 + 0*8 + 0*4 + 1*2
+ 0*1 =
16 + 0 + 0 + 2 + 0 = 18
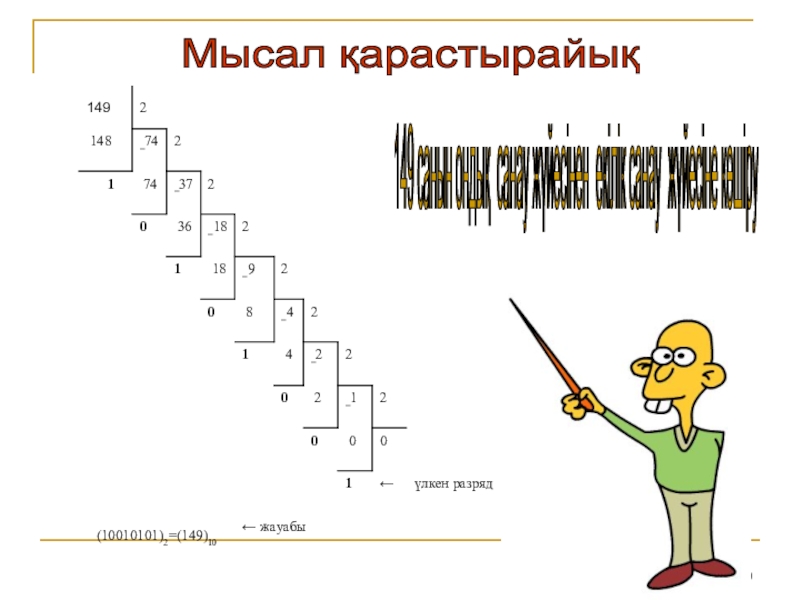
Слайд 40149 санын ондық санау жүйесінен екілік санау жүйесіне көшіру
Мысал
қарастырайық
Слайд 41
149 санын екіге бөліп 74 санын аламыз, қалдық 1
74
санын екіге бөліп 37 санын аламыз, қалдық 0
Осылайша
бөлетін сан қалмағанша
бөлуді жалғастырамыз
Жауабы:
(10010101)2=(149)10
Қалдықта қалған сандарды ең
соңынан бастап жазамыз
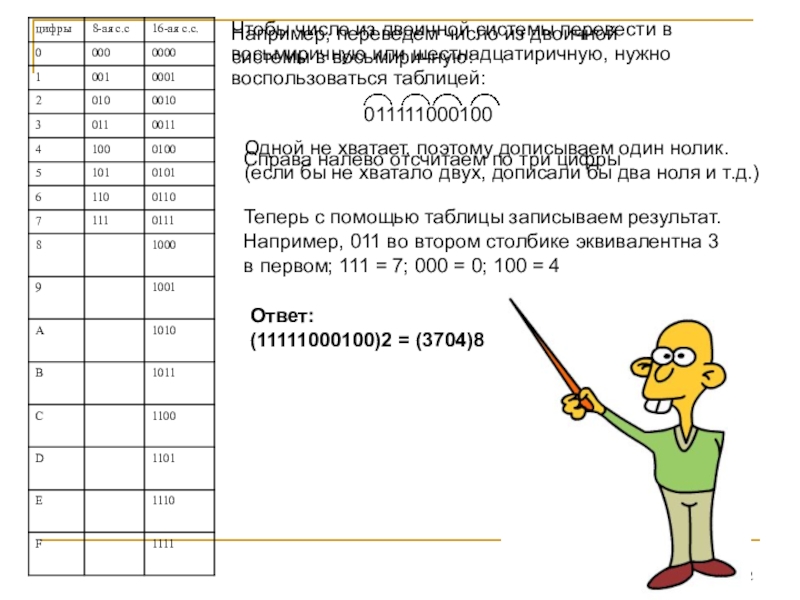
Слайд 42Чтобы число из двоичной системы перевести в восьмиричную или шестнадцатиричную,
нужно воспользоваться таблицей:
Например, переведем число из двоичной
системы в восьмиричную:
11111000100
Справа налево
отсчитаем по три цифры
Одной не хватает, поэтому дописываем один нолик.
(если бы не хватало двух, дописали бы два ноля и т.д.)
0
Теперь с помощью таблицы записываем результат.
Например, 011 во втором столбике эквивалентна 3
в первом; 111 = 7; 000 = 0; 100 = 4
Ответ:
(11111000100)2 = (3704)8
Слайд 4311111000100
0
Санды 16-лық санау жүйесіне ауыстыру үшін,осы операцияларды қайталаймыз
Бірақ бұл жолы
сандарды оңнан
солға қарай төрт төрттен бөлеміз
жауабы: (7С4)16
Слайд 44x
Санды он алтылық санау жүйесінен ондық санау жүйесіне ауыстыру
0
1
b
4
#
0
b
16
1
4
+
16
1
+
16
4
=75
x
x
11
x
Слайд 45
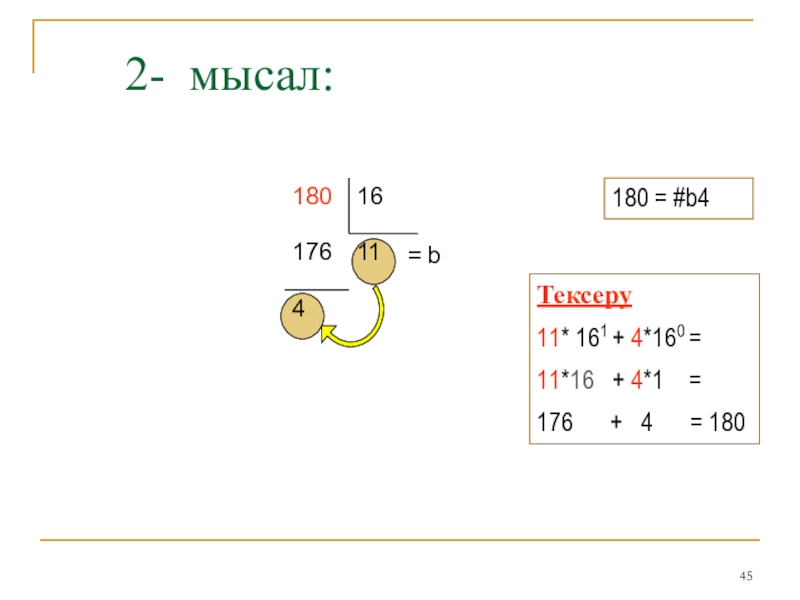
2- мысал:
4
11
176
16
180
180 = #b4
Тексеру
11* 161 + 4*160 =
11*16
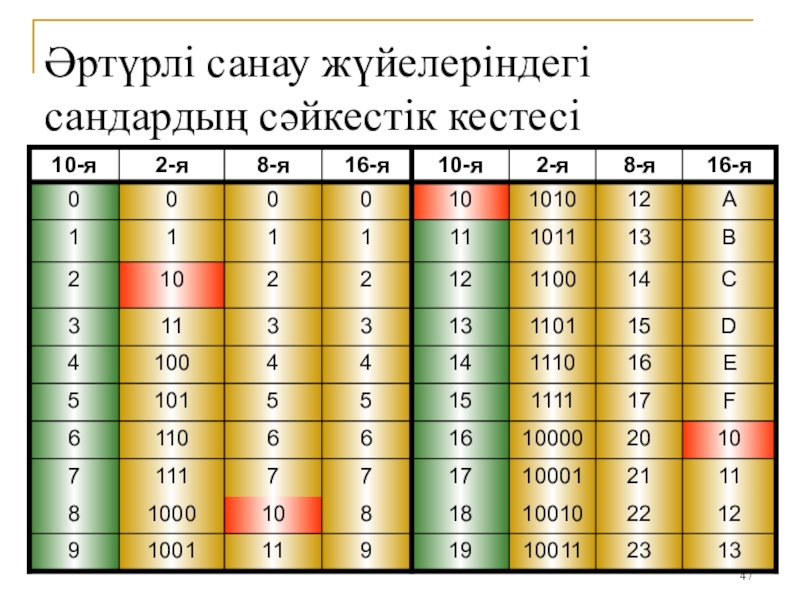
Слайд 47Әртүрлі санау жүйелеріндегі сандардың сәйкестік кестесі
Слайд 48СҰРАҚ
Санау жүйесінде арифметикалық амалдар қалай орындалады?
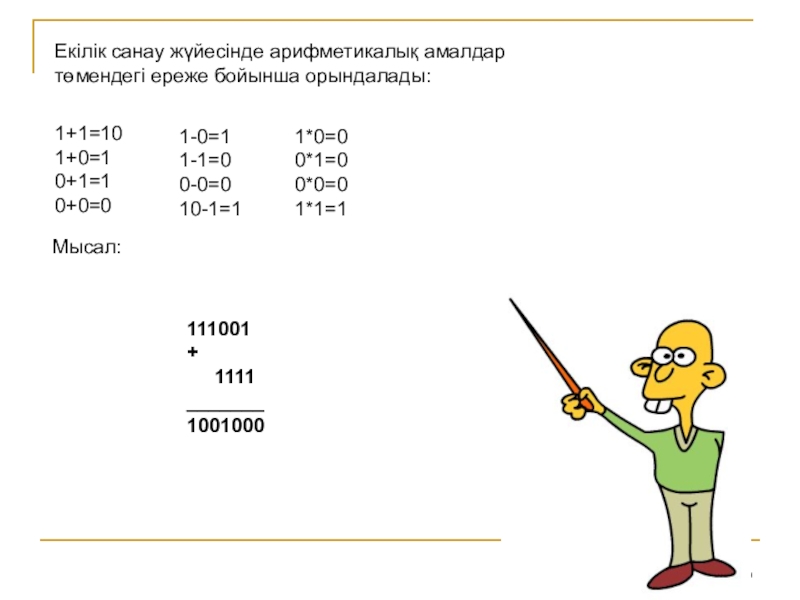
Слайд 49Екілік санау жүйесінде арифметикалық амалдар
төмендегі ереже бойынша орындалады:
1+1=10
1+0=1
0+1=1
0+0=0
1-0=1
1-1=0
0-0=0
10-1=1
1*0=0
0*1=0
0*0=0
1*1=1
Мысал:
111001
+
1111
_______
1001000
Слайд 52Задача 1
В бумагах одного чудака найдена была его
автобиография. Она начиналась следующими строками:
«Я окончил курс университета 44
лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте всего 11 лет способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей.»
Попробуйте разгадать ее.
Слайд 53Для хранения области экрана монитора размером 256х128 точек выделено 32
Kb оперативной памяти. Количество цветов, максимально допустимое для раскраски каждой
точки: 4; 16; 256; 512 ?
Задача 2
1. Всего точек = 128*256 = 27*28=215
2. Всего памяти = 32Kb = 32*210b = 25*210b = 215b
3. Памяти на одну точку = 215b / 215 = 1b = 8 бит
4. Комбинаций на основании 8 бит = 28 = 256
ОЙ!
Слайд 54Досье на сотрудников занимают 8 Mb. Каждое из них содержит
16 страниц (32 строки по 64 символа в строке). Сколько
сотрудников в организации:
256; 512; 1024; 2048?
Задача 3
1. Символов 1 д. = 16*32*64 = 24*25*26=215
3. Всего = 8Mb = 23*220b = 223b
4. Кол-во сотр. = 223b / 215b = 28 = 256
1 символ = 1b
2. Памяти на 1 д. = 215b
ОЙ!
Слайд 55Назарларыңызға размет!!!
Тақырыпты дайындаған:
информатика кафедрасының доценті
Кубентаева С.Н.
С.Аманжолов атындағы ШҚМУ
2007
год