Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления
Содержание
- 1. Системы счисления
- 2. Система счисления (с/с)-это совокупность приемов и правил изображения чисел цифровыми знаками.
- 3. Арифметика каменного векаЕдиничная система счисления (унарная)10 - 11 тыс. лет до н. э.=
- 4. Древнегреческая нумерацияВ V веке до н.э. появилась алфавитная нумерация.Пример:
- 5. Славянская кириллическая нумерацияПример:
- 6. Римская система счисленияПример:DC-XV=DLXXXV
- 7. Египетская нумерация1 10
- 8. Системы счисленияПозиционные системы счисленияНепозиционные системы счисления
- 9. В позиционной системе счисления значение каждой цифры
- 10. Какая система счисления используется повсеместно в наше
- 11. Двенацетиричная (количество месяцев в году, количество часов,
- 12. В непозиционной системе счисления значение цифры не
- 13. Римская непозиционная система счисленияI (1)V (5)X (10)L (50)C (100)D (500)M (1000)
- 14. Значение цифры не зависит от ее местоположения в числеXXX = 30MCMXCVIII = 1000+(1000-100)+(100-10)+5+1+1+1=1998
- 15. В ЭВМ вся исходная, промежуточная и окончательная информация представляется в виде совокупности цифр.
- 16. В ЭВМ применяются позиционные системы счисления:Двоичная система
- 17. Системы счисления отличаются друг от друга количеством
- 18. Двоичная – 0, 1 (основание с.с. –
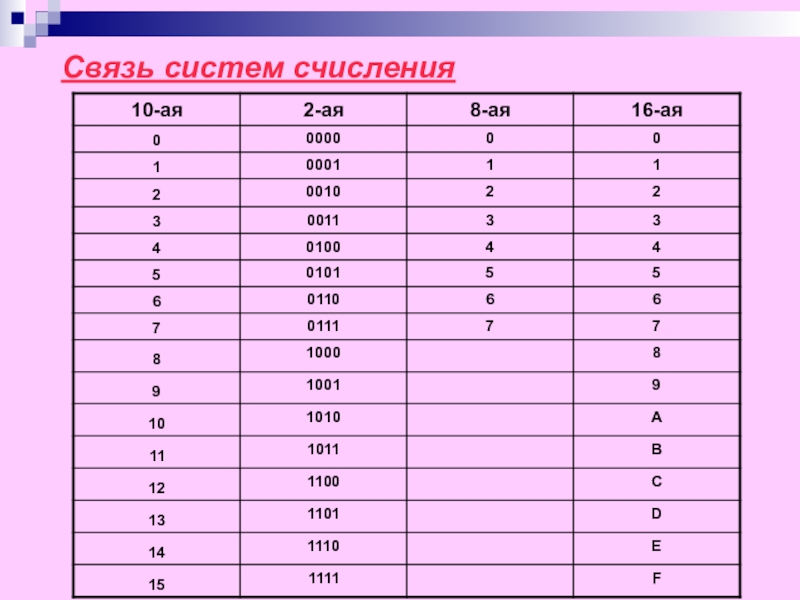
- 19. Связь систем счисления
- 20. Правила переводаИз десятичной системы счисления в позиционные
- 21. Представим число 67 записанное в десятичной системе
- 22. Представим число 6710 в двоичной системе счисления:331168421Ответ: 6710 = 10000112
- 23. 67Представим число 6710 в восьмеричной системе счисления:831Ответ: 6710 = 1038
- 24. Представим число 6710 в шестнадцатеричной системе счисления:674Ответ: 6710 = 4316
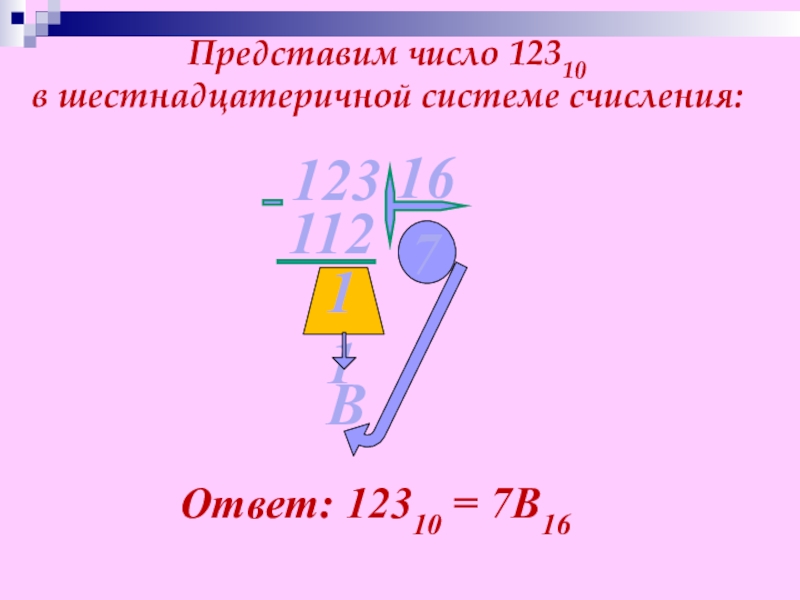
- 25. Представим число 12310 в шестнадцатеричной системе счисления:711ВОтвет: 12310 = 7В16
- 26. Представим число 42 записанное в десятичной системе
- 27. Перевод десятичного числа в другую позиционную систему счисления
- 28. Правила перевода Из любой позиционной системы
- 29. Представим число 10000112 в десятичной системе счисления:Ответ: 10000112=671016050403021110 = 1∙20+1∙21+0∙22+0∙23+0∙24+0∙25+1∙26= 1+2+0+0+0+0+64= 6710 а0=1Свойство степени
- 30. Представим число 1038 в десятичной системе счисления:Ответ: 1038=6710120130= 3∙80+0∙81+1∙82=3+0+64=6710
- 31. Представим число 7В16 в десятичной системе счисления:Ответ: 7В16 = 12310 71В0 = 11∙160+7∙161=11+112=12310
- 32. Между 2-ой и 16-ой с/с есть характерная
- 33. Представим число 11100011012 в шестнадцатеричной
- 34. Правила перевода Из двоичной системы
- 35. Представим число 10110001102 в восьмеричной
- 36. Арифметические операции в системах счисления
- 37. Мысленно переложить одну спичку так, чтобы получилось
- 38. Сложение 0+0=0 0+1=1 1+0=1 1+1=0 +1 в
- 39. СложениеПри сложении 2-ых чисел в каждом разряде
- 40. Пример сложения:
- 41. ВычитаниеПри вычитании 2-ых чисел в данном разряде
- 42. Пример вычитания:
- 43. УмножениеУмножение 2-ых многоразрядных чисел производится путем образования
- 44. Пример умножения:
- 45. Скачать презентанцию
Система счисления (с/с)-это совокупность приемов и правил изображения чисел цифровыми знаками.
Слайды и текст этой презентации
Слайд 2Система счисления (с/с)-
это совокупность приемов и правил изображения чисел цифровыми
знаками.
Слайд 9В позиционной системе счисления значение каждой цифры определяется её положением
(позицией в числе).
Примером позиционной системой счисления является 10-ая система
счисления.Слайд 10Какая система счисления используется повсеместно в наше время?
Сколько цифр в
десятичной системе?
Какие это цифры?
Как вы думаете, почему люди используют десятичную
систему, а не семеричную?Слайд 11Двенацетиричная (количество месяцев в году, количество часов, количество знаков зодиака);
Семеричная (семь дней в неделе, обилие пословиц и поговорок с
числом семь);Шестидесятеричная система счисления (временная мера)
Вспомните, какие системы счисления встречаются в нашей жизни по сей день?
Слайд 12В непозиционной системе счисления значение цифры не зависит от ее
положения в числе.
Примером непозиционной системой счисления является римская система счисления.
Слайд 14Значение цифры не зависит от ее местоположения в числе
XXX =
30
MCMXCVIII = 1000+(1000-100)+(100-10)+5+1+1+1=1998
Слайд 15
В ЭВМ вся исходная, промежуточная и окончательная информация представляется в
виде совокупности цифр.
Слайд 16В ЭВМ применяются позиционные системы счисления:
Двоичная система счисления (2-ая с/с)
Восьмеричная
система счисления (8-ая с/с)
Десятичная система счисления (10-ая с/с)
Шестнадцатеричная система счисления
(16-ая с/с)Слайд 17Системы счисления отличаются друг от друга количеством цифр, т.е. основанием.
Основание
системы счисления – это количество цифр, которыми обозначаются числа.
Слайд 18Двоичная – 0, 1 (основание с.с. – 2)
Десятичная – 0,
1, 2, 3, 4, 5, 6, 7, 8, 9 (основание
с.с. – 10)Восьмеричная – 0, 1, 2, 3, 4, 5, 6, 7 (основание с.с. – 8)
Шестнадцатеричная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F (основание с.с. – 16)
Слайд 20Правила перевода
Из десятичной системы счисления
в позиционные системы счисления:
Разделить десятичное
число на основание новой системы счисления. Получится частное и остаток.
Остаток
от деления переводят в новую систему счисления – это будет младший разряд нового числа.Выполнять деление до тех пор, пока последнее частное не станет меньшим основания новой системы счисления.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет записью в новой системы счисления.
Слайд 21Представим число 67 записанное в десятичной системе счисления в позиционных
системах счисления:
двоичной, восьмеричной, шестнадцатеричной.
6710 = А2
6710 = А8
6710 = А16
Слайд 26Представим число 42 записанное в десятичной системе счисления в позиционных
системах счисления:
двоичной, восьмеричной, шестнадцатеричной.
4210 = А2
4210 = А8
4210 = А16
Слайд 28
Правила перевода
Из любой позиционной системы счисления в десятичную систему счисления:
Запись
числа в 10-ой с/с означает представление этого числа в виде
суммы степеней основания с различными коэффициентами.2 1 0
Например: 4 5 6 8
Слайд 29Представим число 10000112
в десятичной системе счисления:
Ответ: 10000112=6710
16050403021110 = 1∙20+1∙21+0∙22+0∙23+0∙24+0∙25+1∙26=
1+2+0+0+0+0+64= 6710
а0=1
Свойство степени
Слайд 30Представим число 1038
в десятичной системе счисления:
Ответ: 1038=6710
120130= 3∙80+0∙81+1∙82=3+0+64=6710
Слайд 31Представим число 7В16
в десятичной системе счисления:
Ответ: 7В16 = 12310
71В0 = 11∙160+7∙161=11+112=12310
Слайд 32Между 2-ой и 16-ой с/с есть характерная связь (24=16), позволяющая
переводить числа простым способом – по таблице, представляя их по
4 разряда начиная с младшего.
Правила перевода
Из двоичной системы счисления в шестнадцатеричную систему счисления и обратно:
Слайд 33
Представим число 11100011012 в шестнадцатеричной системе счисления:
0011 1000 11012
⭢ 38D16
13 → D
Представим число 36816 в двоичной
системе счисления:
36816
→ 0011 0110 1000 2Слайд 34 Правила перевода Из двоичной системы счисления в восьмеричную систему счисления и
обратно:
Между 2-ой и 8-ой с/с есть характерная связь (23=8), позволяющая
переводить числа простым способом – по таблице, представляя их по 3 разряда (левый ноль отбрасывается) начиная с младшего.Слайд 35
Представим число 10110001102 в восьмеричной системе счисления:
001 011 000
1102 ⭢ 13068
Представим число 3614 в двоичной
системе счисления:
3614 8
→ 011 110 001 100 2Слайд 37Мысленно переложить одну спичку так, чтобы получилось верное равенство
а) VII – V = XI
б)
IX – V = VI в) VIII – III = X
Слайд 38Сложение
0+0=0
0+1=1
1+0=1
1+1=0 +1 в старший разряд
3. Умножение
0•0=0
1•0=0
0•1=0
1•1=1
Арифметика с двоичными числами
2. Вычитание
0-0=0
0-1=1 -1 из старщего разряда
1-0=1
1-1=0
Слайд 39Сложение
При сложении 2-ых чисел в каждом разряде в соответствии с
таблицей сложения производится сложение 2-ух цифр слагаемых или 2-ух этих
цифр и 1, если есть перенос из младшего разряда.В результате получается цифра соответствующего разряда суммы и, возможно, переноса в старший разряд.
Слайд 41Вычитание
При вычитании 2-ых чисел в данном разряде при необходимости занимается
1 из старшего разряда. Эта 1 равна 2 единицам данного
разряда.Заем производится каждый раз, когда цифра в разряде вычитаемого больше цифры в том же разряде уменьшаемого.
Слайд 43Умножение
Умножение 2-ых многоразрядных чисел производится путем образования частичных произведений и
последующего их суммирования.
В соответствии с таблицей двоичного умножения каждое частичное
произведение равно 0, если в соответствующем разряде множимого стоит 0.Т.о. операция умножения сводится к операциям сдвига и сложения.