Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления. Быстрый перевод из десятичной системы счисления в двоичную.
Содержание
- 1. Системы счисления. Быстрый перевод из десятичной системы счисления в двоичную.
- 2. Быстрый перевод числа из десятичной системы счисления
- 3. Примеры: Переведем число 2 из десятичной системы.
- 4. Слайд 4
- 5. Аналогично и для других чисел "2 в степени".Если
- 6. Аналогичен перевод и для других чисел "2 в
- 7. Если число больше, то решаем так: Переводим сначала
- 8. Если число меньше числа "2 в степени", то удобнее
- 9. Если разница между переводимым числом и числом "2
- 10. Разбор задачи A1 (демо ЕГЭ 2013)Сколько единиц
- 11. Если число меньше числа "2 в степени",
- 12. Если разница между переводимым числом и числом
- 13. 2 способ (метод быстрого перевода):Метод описан в
- 14. Тестирование по темеhttp://inf.reshuege.ru/test?a=catlistwstat
- 15. Источникистатья: "Быстрый перевод числа из десятичной системы счисления в двоичную".демо ЕГЭ 2012 года.http://reshuege.ruhttp://tidm.ru
- 16. Скачать презентанцию
Быстрый перевод числа из десятичной системы счисления в двоичнуюЧтобы быстро переводить числа из десятичной системы счисления в двоичную, нужно хорошо знать числа "2 в степени". В зависимости от того как отличается
Слайды и текст этой презентации
Слайд 2Быстрый перевод числа из десятичной системы счисления в двоичную
Чтобы быстро
переводить числа из десятичной системы счисления в двоичную, нужно хорошо
знать числа "2 в степени".В зависимости от того как отличается переводимое число от числа «2 в степени» существует несколько методов перевода.
Метод 1 если число, которое нужно перевести из десятичной системы, равно числу "2 в степени", то это число в двоичной системе содержит количество нулей, равное степени. Впереди этих нулей добавляем "1".
Слайд 3Примеры:
Переведем число 2 из десятичной системы.
2=21. Поэтому в двоичной
системе число содержит 1 нуль. Впереди ставим "1" и получаем 102.
Переведем
4 из десятичной системы. 4=22. Поэтому в двоичной системе число содержит 2 нуля. Впереди ставим "1" и получаем 1002.
Переведем 8 из десятичной системы.
8=23. Поэтому в двоичной системе число содержит 3 нуля. Впереди ставим "1" и получаем 10002.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Слайд 5Аналогично и для других чисел "2 в степени".
Если число, которое нужно
перевести, меньше числа "2 в степени" на 1, то в
двоичной системе это число состоит только из единиц, количество которых равно степени.Переведем 3 из десятичной системы. 3=22-1. Поэтому в двоичной системе число содержит 2 единицы. Получаем 112.
Переведем 7 из десятичной системы. 7=23-1. Поэтому в двоичной системе число содержит 3 единицы. Получаем 1112.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Слайд 6Аналогичен перевод и для других чисел "2 в степени-1".
Понятно, что перевод
чисел от 0 до 8 можно сделать быстро или делением,
или просто знать наизусть их представление в двоичной системе. Этот метод можно использовать для перевода более "внушительных чисел", например, для перевода чисел 127,128, 255, 256, 511, 512 и т.д.Можно встретить такие задачи, когда нужно перевести число, не равное числу "2 в степени", но близкое к нему. Оно может быть больше или меньше числа "2 в степени". Разница между переводимым числом и числом "2 в степени" должна быть небольшая. Например, до 3. Представление чисел от 0 до 3 в двоичной системе надо просто знать без перевода.
Слайд 7Если число больше, то решаем так:
Переводим сначала число "2 в степени"
в двоичную систему. А потом прибавляем к нему разницу между
числом "2 в степени" и переводимым числом.Например, переведем 19 из десятичной системы. Оно больше числа "2 в степени" на 3.
19=16+3.
16=24. 1610=100002.
310=112.
1910=100002+112=100112.
Слайд 8Если число меньше числа "2 в степени", то удобнее пользоваться числом "2
в степени-1". Решаем так:
Переводим сначала число "2 в степени-1" в
двоичную систему. А потом вычитаем из него разницу между числом "2 в степени-1" и переводимым числом.Например, переведем 29 из десятичной системы. Оно больше числа "2 в степени-1" на 2. 29=31-2.
3110=111112.
210=102.
2910=111112-102=111012
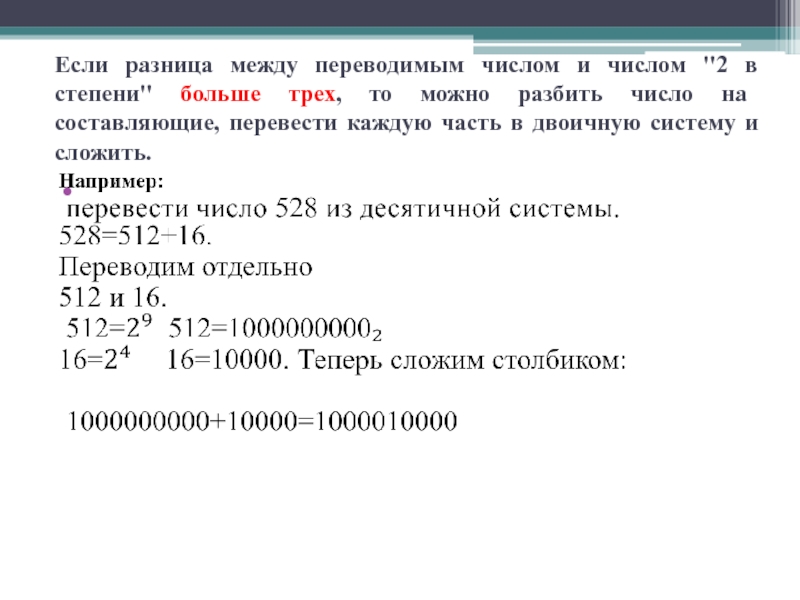
Слайд 9Если разница между переводимым числом и числом "2 в степени" больше трех,
то можно разбить число на составляющие, перевести каждую часть в
двоичную систему и сложить.Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16. 512=29 . 51210=10000000002. 16=24. 1610=100002. Теперь сложим столбиком:
Данная методика позволяет тратить минимум времени на перевод чисел из десятичной системы в двоичную, но при условии, что Вы прекрасно знаете числа "2 в степени". Если это не так, то заучите эти числа. Тем более, что в задачах по информатике они активно используются.
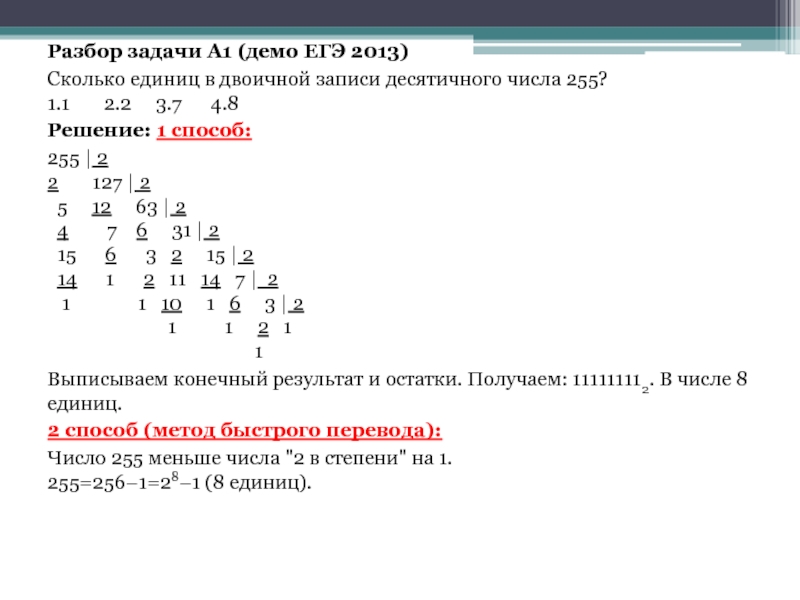
Слайд 10Разбор задачи A1 (демо ЕГЭ 2013)
Сколько единиц в двоичной записи
десятичного числа 255? 1.1 2.2 3.7
4.8Решение: 1 способ:
255 | 2 2 127 | 2 5 12 63 | 2 4 7 6 31 | 2 15 6 3 2 15 | 2 14 1 2 11 14 7 | 2 1 1 10 1 6 3 | 2 1 1 2 1 1
Выписываем конечный результат и остатки. Получаем: 111111112. В числе 8 единиц.
2 способ (метод быстрого перевода):
Число 255 меньше числа "2 в степени" на 1. 255=256−1=28−1 (8 единиц).
Слайд 11Если число меньше числа "2 в степени", то удобнее пользоваться
числом "2 в степени-1".
Решаем так: Переводим сначала число "2 в
степени-1" в двоичную систему. А потом вычитаем из него разницу между числом "2 в степени-1" и переводимым числом.Например: переведем 29 из десятичной системы.
Оно больше числа "2 в степени-1" на 2.
29=31-2.
31=11111₂
2=10₂
29=11111₂-10₂=11101₂
Слайд 12Если разница между переводимым числом и числом "2 в степени"
больше трех, то можно разбить число на составляющие, перевести каждую
часть в двоичную систему и сложить.Слайд 132 способ (метод быстрого перевода):
Метод описан в статье: "Быстрый перевод числа
из десятичной системы счисления в двоичную".
Число 255 меньше числа "2
в степени" на 1.255=256−1=28−1 (8 единиц).