Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сжатие информации Алгоритм Хаффмана
Содержание
- 1. Сжатие информации Алгоритм Хаффмана
- 2. Сжатие информацииСжатие данных – сокращение объема данных при сохранении закодированного в них содержания.
- 3. Сжатие информацииСжатие происходит за счет устранения избыточности
- 4. Алгоритмы сжатия1. Равномерное сжатие с использованием кодов
- 5. Сжатие с использованием кодов переменной длиныВ этом
- 6. Префиксные кодыЧтобы понять, как строятся префиксные коды,
- 7. Префиксные кодыПостроим граф этого кода.Из начальной вершины
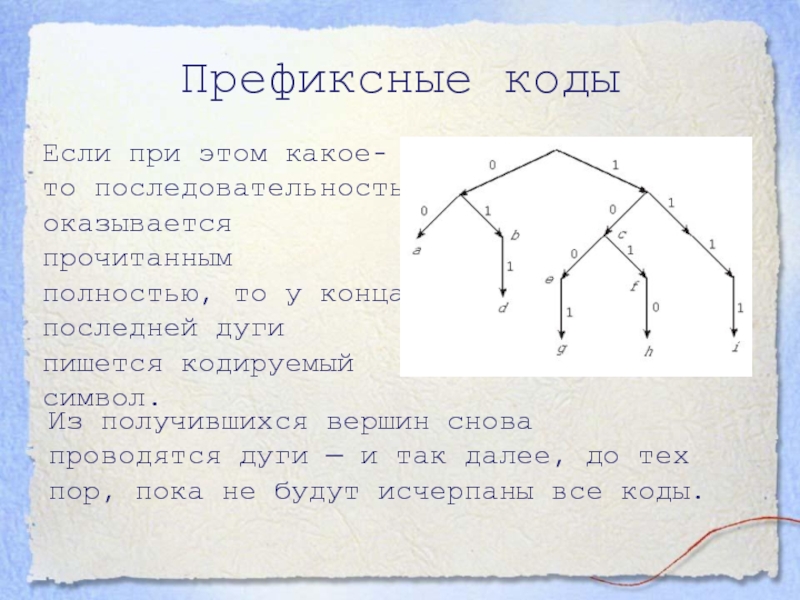
- 8. Префиксные кодыЕсли при этом какое-то последовательность оказывается
- 9. Префиксные кодыЕсли известен граф, созданный по префиксному
- 10. Алгоритм ХаффманаАлгоритм Хаффмана — адаптивный алгоритм оптимального префиксного кодирования алфавита с
- 11. 1. Символы исходного алфавита образуют вершины. Вес
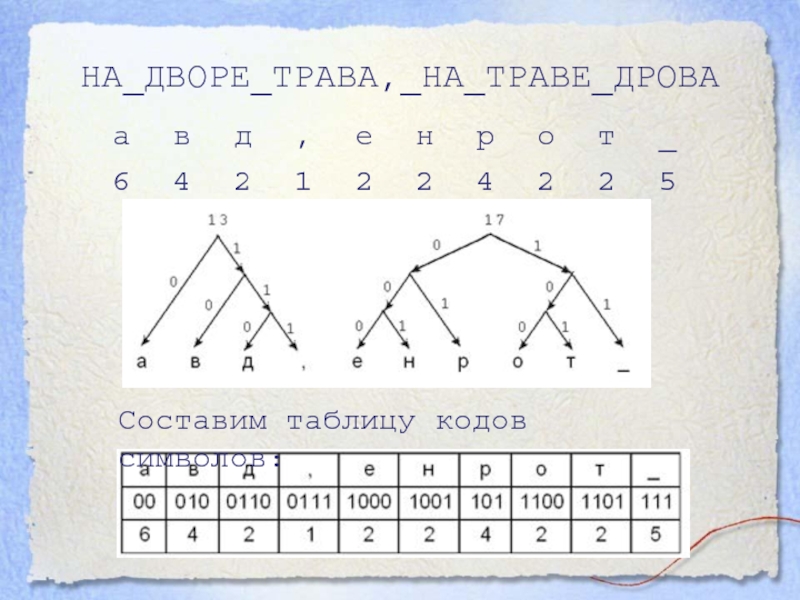
- 12. НА_ДВОРЕ_ТРАВА,_НА_ТРАВЕ_ДРОВА Составим таблицу кодов символов:
- 13. Найдем объем сообщения после кодирования кодом Хаффмана:
- 14. Математики доказали, что среди алгоритмов, кодирующих каждый
- 15. Для кодирования сообщения, состоящего из букв А,
- 16. Задача А9. Решение.Построим двоичное дерево, в котором
- 17. Задача А9. Решение.По дереву определим, что для
- 18. Для передачи по каналу связи сообщения, состоящего
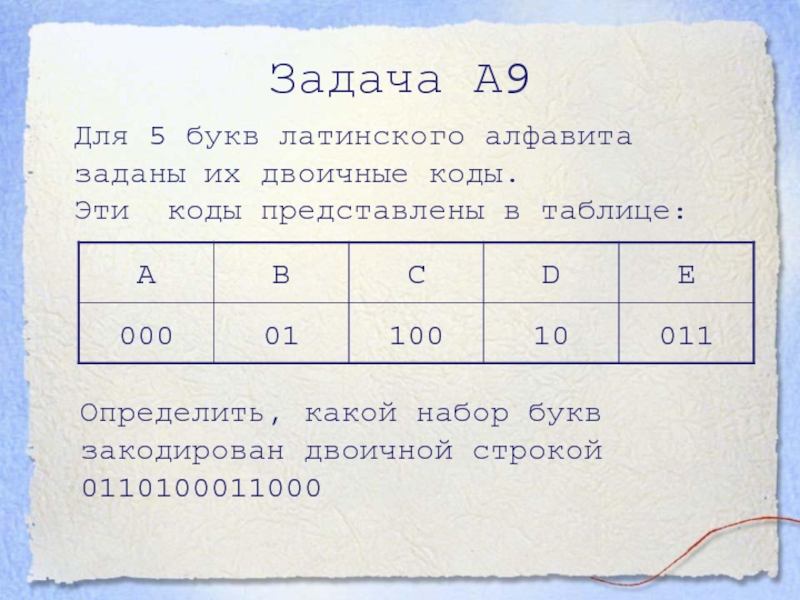
- 19. Для 5 букв латинского алфавита заданы их
- 20. Для передачи по каналу связи сообщения, состоящего
- 21. Скачать презентанцию
Сжатие информацииСжатие данных – сокращение объема данных при сохранении закодированного в них содержания.
Слайды и текст этой презентации
Слайд 2Сжатие информации
Сжатие данных – сокращение объема данных при сохранении закодированного
в них содержания.
Слайд 3Сжатие информации
Сжатие происходит за счет устранения избыточности кода, например, за
счет упрощения кодов, исключения из них постоянных битов или представления
повторяющихся символов в виде коэффициента повторения.Важнейшая характеристика процесса сжатия – коэффициент сжатия.
Коэффициент сжатия – отношение объема исходного сообщения к объему сжатого.
Слайд 4Алгоритмы сжатия
1. Равномерное сжатие с использованием кодов одной длины.
Этот метод
используется, если в записи сообщения присутствует небольшая часть алфавита.
2. Сжатие
с использованием кодов переменной длины. Сокращение объёма данных достигается за счёт замены часто встречающихся данных короткими кодовыми словами, а редких — длинными.
Слайд 5Сжатие с использованием кодов переменной длины
В этом случае возникает проблема
отделения кодов символов друг от друга.
Решить эту проблему позволяет
условие, достаточное для однозначного декодирования сообщений с переменной длиной кодовых слов, условие Фано: Никакое кодовое слово не является началом другого кодового слова.
По-другому условие Фано называют свойством префиксности, а код, удовлетворяющий этому условию, называют префиксным кодом.
Слайд 6Префиксные коды
Чтобы понять, как строятся префиксные коды, рассмотрим, как построить
ориентированный граф, определяющий этот код.
Например, кодовые слова 00, 01,
10, 011, 100, 101, 1001, 1010, 1111, кодируют соответственно буквы: a, b, c, d, e, f, g, h, i. Слайд 7Префиксные коды
Построим граф этого кода.
Из начальной вершины выходят две дуги,
помеченные 0 и 1. Затем из конца каждой такой дуги
входят новые дуги, помеченные 0 и 1 так, чтобы, идя по этим дугам от корня, читалось начало какого-либо кодового слова.Слайд 8Префиксные коды
Если при этом какое-то последовательность оказывается прочитанным полностью, то
у конца последней дуги пишется кодируемый символ.
Из получившихся вершин
снова проводятся дуги — и так далее, до тех пор, пока не будут исчерпаны все коды. Слайд 9Префиксные коды
Если известен граф, созданный по префиксному коду, то по
этому графу легко восстанавливается код каждого символа — надо просто,
идя от корня к листу, помеченному данным символом, выписать 0 и 1 в порядке их прочтения.Идея префиксного кодирования была использована американским ученым Д.Хаффманом для создания эффективного алгоритма сжатия символьной информации.
Слайд 10Алгоритм Хаффмана
Алгоритм Хаффмана — адаптивный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью.
Был
разработан 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В
настоящее время используется во многих программах сжатия данных.Слайд 111. Символы исходного алфавита образуют вершины. Вес каждой вершины вес
равен количеству вхождений данного символа в сжимаемое сообщение.
2. Среди вершин
выбираются две с наименьшими весами (если таких пар несколько, выбирается любая из них).3. Создается следующая вершина графа, из которой выходят две дуги к выбранным вершинам; одна дуга помечается цифрой 0, другая — символом 1.
Вес созданной вершины равен сумме весов, выбранных на втором шаге вершин.
4. К новым вершинам применяются шаги 2 и 3 до тех пор, пока не останется одна вершина с весом, равным сумме весов исходных символов.
Слайд 13Найдем объем сообщения после кодирования кодом Хаффмана: 2·6 + 3·4
+ 4·2 + 4·1 + 4·2 + 4·2 + 3·4
+ 4·2 + 4·2 + 3·5 = 95 бит.Теперь подсчитаем объем этого сообщения, если каждый его символ кодировать цепочкой из 0 и 1 равной длины. Т.к. в сообщении 10 различных символов вес одного символа 4 бита. Поэтому после кодирования получится сообщение объемом 4·3 = 120 бит.
Коэффициент сжатия равен 120/95 =1,26.
Сообщение в памяти компьютера закодировано с помощью ASCII-кодов, каждый символ весит 8 бит. Значит, объем исходного сообщения 240 бит.
Коэффициент сжатия равен 240/95 = 2,53.
Слайд 14Математики доказали, что среди алгоритмов, кодирующих каждый символ по отдельности
и целым количеством бит, алгоритм Хаффмана обеспечивает наилучшее сжатие.
Слайд 15Для кодирования сообщения, состоящего из букв А, Б, В, Г
и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную
двоичную последовательность.А–00, Б–010, В–011, Г–101, Д–111.
Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно?
Выберите правильный вариант ответа.
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
Задача А9
Слайд 16Задача А9. Решение.
Построим двоичное дерево, в котором от каждого узла
отходит две ветки: 0 или 1.
Разместим на дереве буквы А,
Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах:Слайд 17Задача А9. Решение.
По дереву определим, что для букв Г и
Д код можно сократить. Выберем ответ из предложенных вариантов:
1) для
буквы Б – 01 2) это невозможно3) для буквы В – 01 4) для буквы Г – 01
Ответ: 4.
Слайд 18Для передачи по каналу связи сообщения, состоящего только из букв
А, Б, В, Г, решили использовать неравномерный по длине код:
A=0, Б=10, В=110.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
1) 1 2) 1110 3) 111 4) 11
Для самостоятельной работы
Слайд 19Для 5 букв латинского алфавита заданы их двоичные коды.
Эти
коды представлены в таблице:
Задача А9
Определить, какой набор букв закодирован двоичной
строкой 0110100011000Слайд 20Для передачи по каналу связи сообщения, состоящего только из букв
А, Б, В, Г, решили использовать неравномерный по длине код:
A=0, Б=10, В=110.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
Задача А9