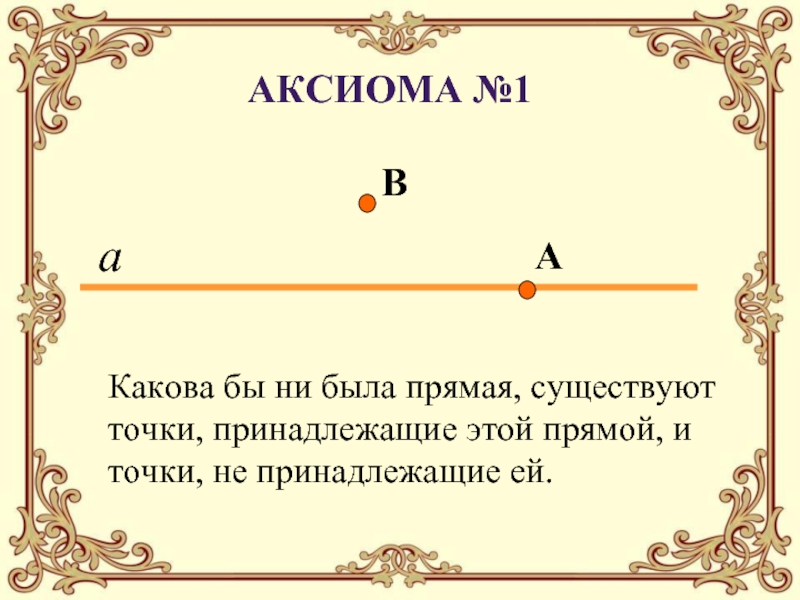
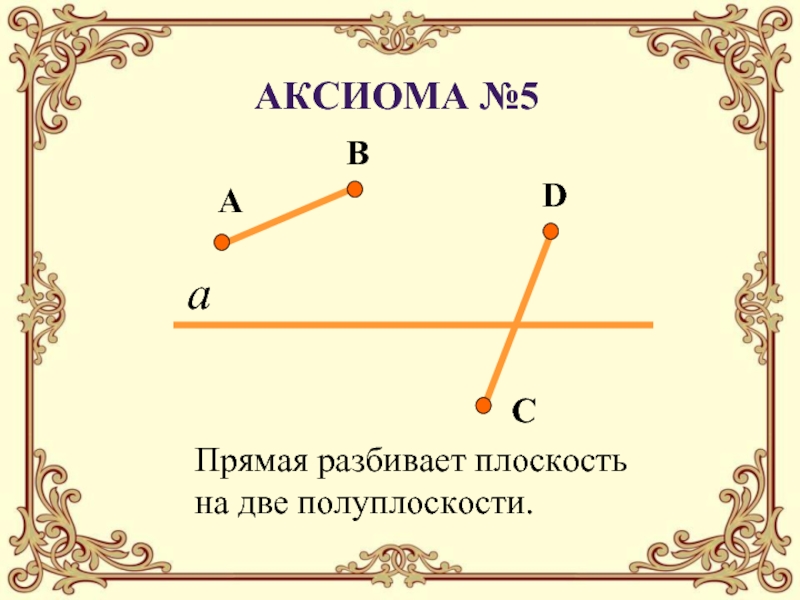
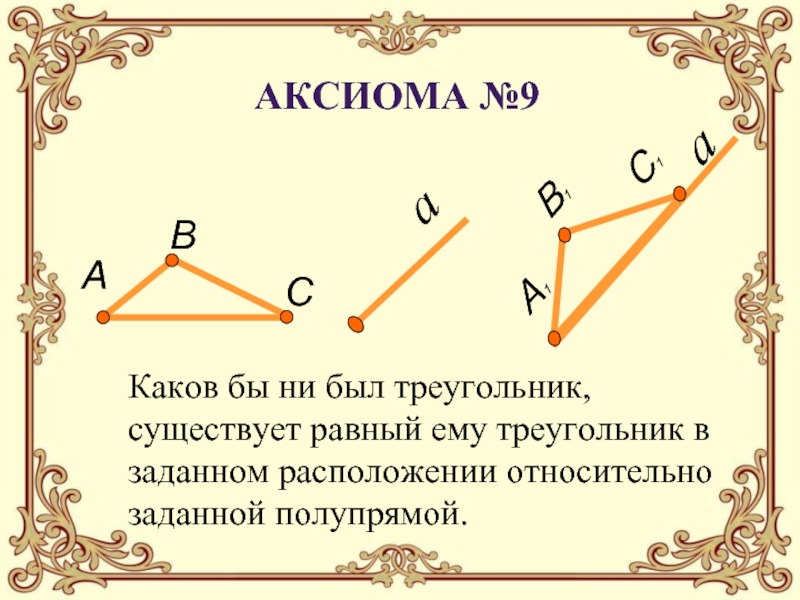
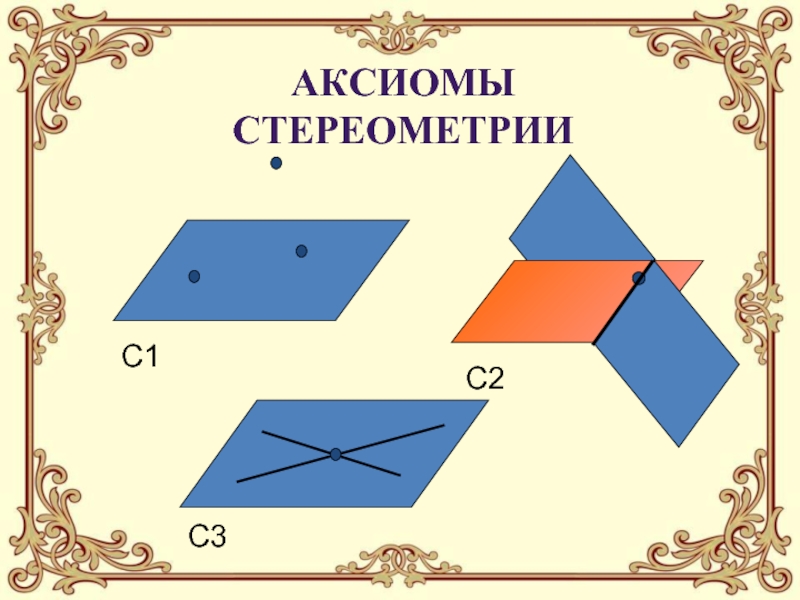
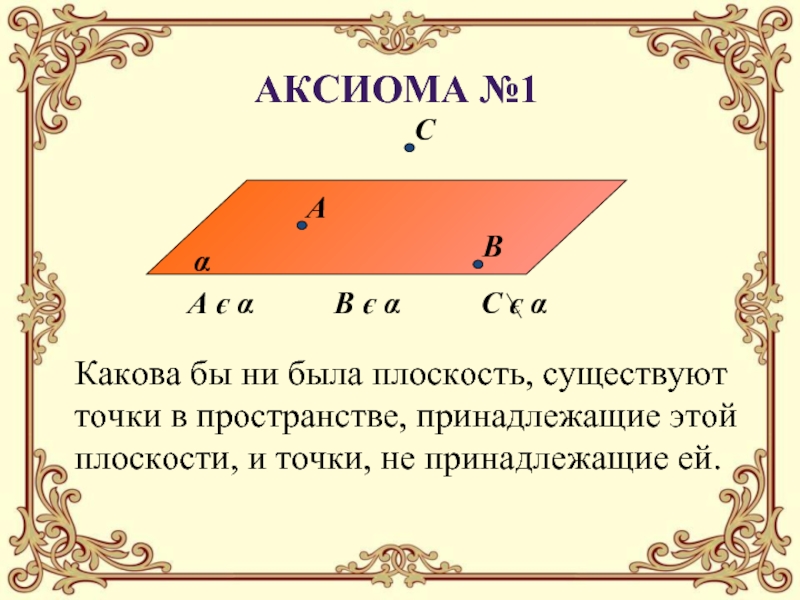
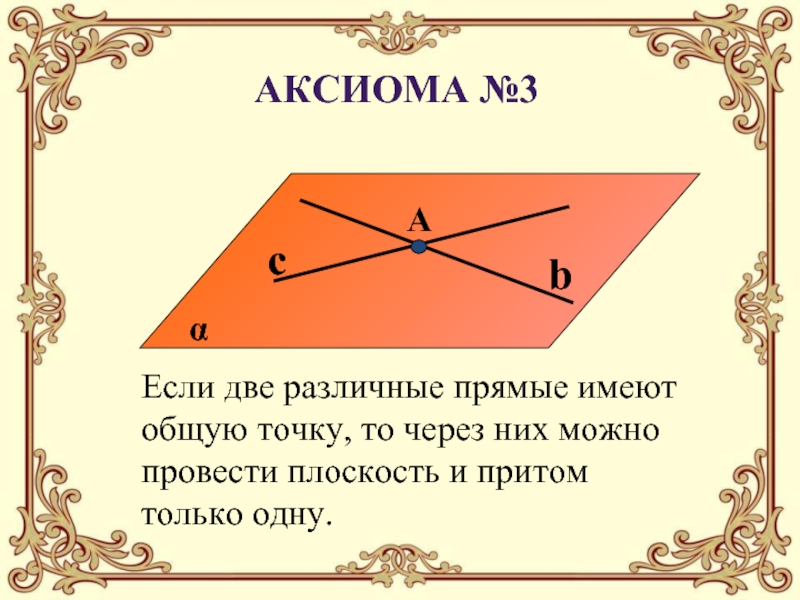
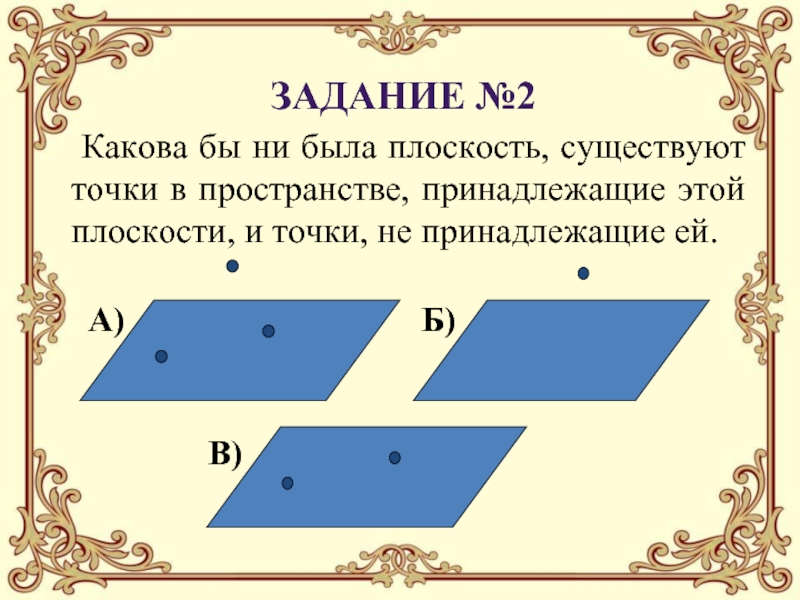
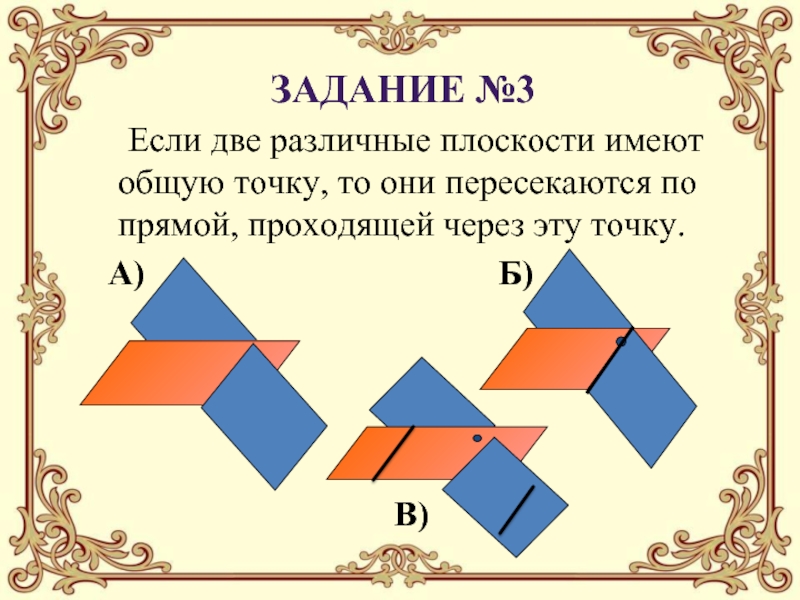
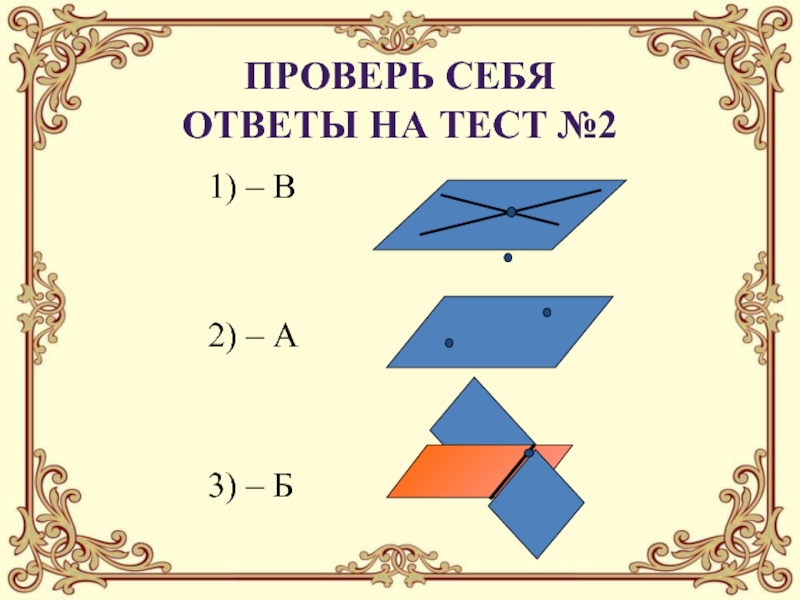
с графическим изображением
Уметь формулировать ответы, используя строгость математического языка
Продолжать учиться
работать в группахСовершенствовать навыки работы с тестами
Цели урока