Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Матрицы и действия с ними
Содержание
- 1. Матрицы и действия с ними
- 2. 1. Определение матрицы Прямоугольная таблица чисел вида называется
- 3. 2. Виды матрицПрямоугольнаяКвадратнаяНулеваяЕдиничнаяДиагональнаяСимметричнаяВырожденнаяРавныеТреугольнаяКвазитреугольная (ступенчатая или трапециевидная)Матрица-строка или строчная матрицаМатрица-столбец или столбцевая матриц
- 4. Матрица называется прямоугольной, если количество ее строк
- 5. Матрица называется нулевой, если все ее элементы
- 6. Квадратная матрица называется диагональной, если элементы по
- 7. Квадратная матрица называется вырожденной, если ее определитель
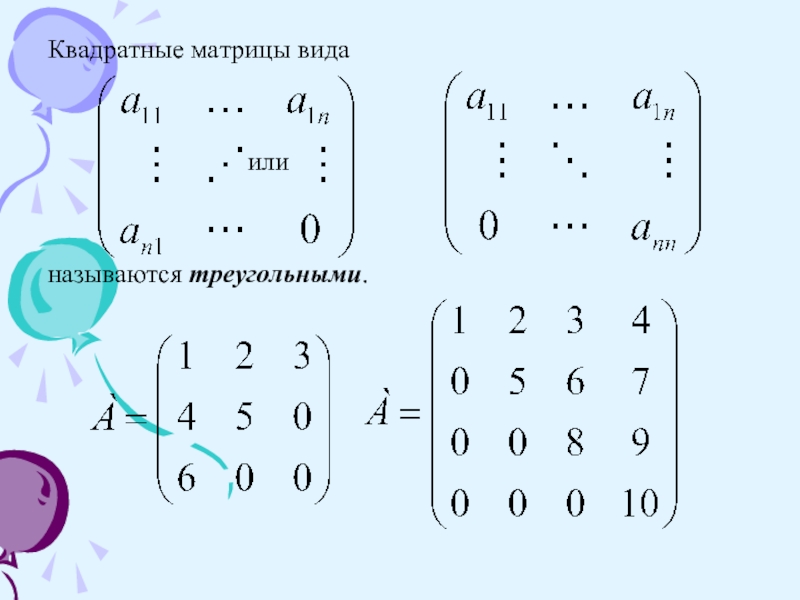
- 8. Квадратные матрицы вида или называются треугольными.
- 9. Прямоугольная матрица вида называется квазитреугольной (ступенчатая или трапециевидная)
- 10. Матрица, состоящая из одной строки называется матрицей-строкой
- 11. Слайд 11
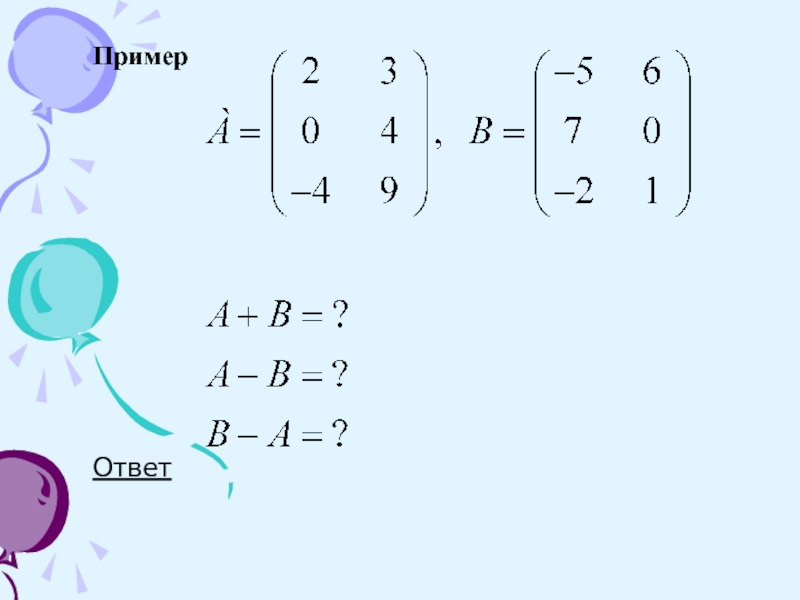
- 12. Суммой (разностью) двух матриц одинаковой размерности называется
- 13. ПримерОтвет
- 14. Произведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число.Например:Пример
- 15. Линейные операции обладают следующими свойствами:
- 16. Матрица, полученная из данной заменой каждой ее
- 17. Умножение матриц определяется для согласованных матриц.Произведением матрицы
- 18. Спасибо за внимание!Презентацию подготовил студент группы СО-11Бирюков Владислав
- 19. Скачать презентанцию
1. Определение матрицы Прямоугольная таблица чисел вида называется матрицей. - элементы матрицы. Размер матрицы Главная диагональ матрицы Побочная диагональ матрицы
Слайды и текст этой презентации
Слайд 1Тема 1. «Матрицы и действия над ними»
Основные понятия:
Определение матрицы
Виды матриц
Действия
над матрицами
Слайд 21. Определение матрицы
Прямоугольная таблица чисел вида
называется матрицей.
- элементы матрицы.
Размер матрицы
Главная диагональ матрицы
Побочная диагональ матрицы
Слайд 32. Виды матриц
Прямоугольная
Квадратная
Нулевая
Единичная
Диагональная
Симметричная
Вырожденная
Равные
Треугольная
Квазитреугольная (ступенчатая или трапециевидная)
Матрица-строка или строчная матрица
Матрица-столбец или
столбцевая матриц
Слайд 4
Матрица называется прямоугольной, если количество ее строк не совпадает с
количеством столбцов:
Матрица называется квадратной, если количество ее строк совпадает с
количеством столбцов:
Слайд 5
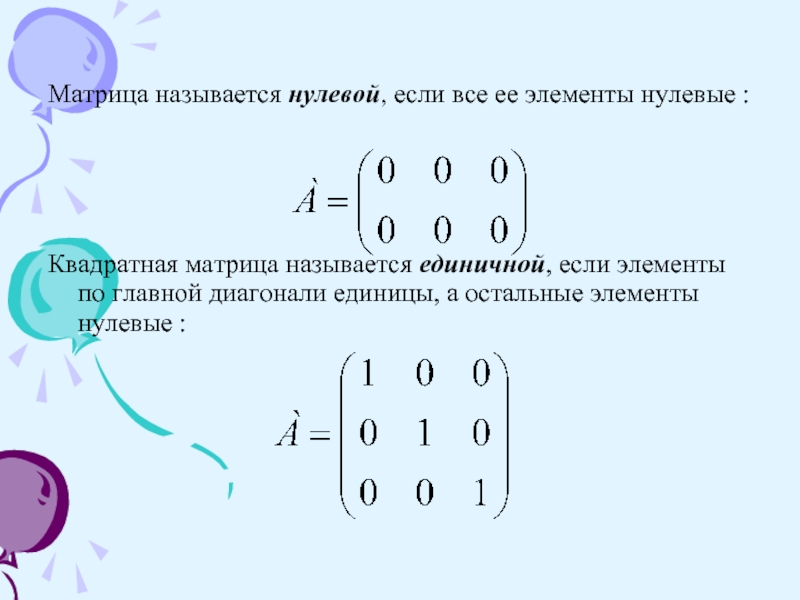
Матрица называется нулевой, если все ее элементы нулевые :
Квадратная матрица
называется единичной, если элементы по главной диагонали единицы, а остальные
элементы нулевые :
Слайд 6Квадратная матрица называется диагональной, если элементы по главной диагонали отличны
от нуля, а остальные элементы нулевые:
Квадратная матрица называется симметричной, если
относительно главной диагонали для всех ее элементов выполняется условие :
Слайд 7
Квадратная матрица называется вырожденной, если ее определитель равен нулю.
Матрицы А
и В (одинаковых размерностей) называются равными, если
:
Слайд 10Матрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей.
Матрица,
состоящая из одного столбца называется матрицей-столбцом или столбцевой матрицей
Слайд 12Суммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой
равны сумме (разности) соответствующих элементов матриц слагаемых.
Например:
Пример
Слайд 14Произведением матрицы на число называется матрица, полученная из данной умножением
всех ее элементов на число.
Например:
Пример
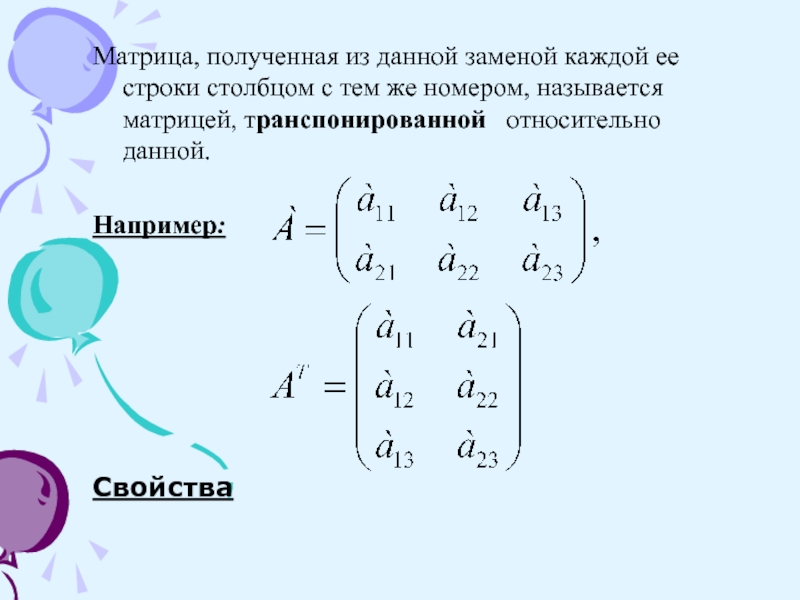
Слайд 16Матрица, полученная из данной заменой каждой ее строки столбцом с
тем же номером, называется матрицей, транспонированной относительно данной.
Например:
Свойства
Слайд 17Умножение матриц определяется для согласованных матриц.
Произведением матрицы
на матрицу
называется матрица , для которой ,т.е. каждый элемент матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Теги