Активные и интерактивные методы обучения как способы активизации учебно-познавательной деятельности учащихся на уроках математики.

Содержание

1. Активные и интерактивные методы обучения как способы активизации учебно-познавательной деятельности учащихся на уроках математики.
2. Дидактические принципы
3. Слайд 3
4. Современный учитель в своей профессиональной
5. Интерактивную доску можно применять на
6. При изучении новой темы можно использовать презентации, видеоматериалы, фотографии.
7. ОПРЕДЕЛЕНИЕ3-угольник + 3 3-угольника4-угольник + 4 3-угольника6-угольник
8. ПРОВЕРЬ СЕБЯВысота - ABCP HОснование -ABCмногоугольник.Боковые грани
9. 1. Сколько боковых рёбер у пятиугольной пирамиды?неверно
10. Работа устно:НЕПРЕ
11. В некотором царстве, в некотором государстве пошёл
12. D(y)=(-∞;+∞)E(y)=(2;+∞) 012345-1-2-3-4-5-1-2-3-4-51234567891011xy=3 -2xy=3 +2xy=3xСдвиг y=3 +2 вдоль
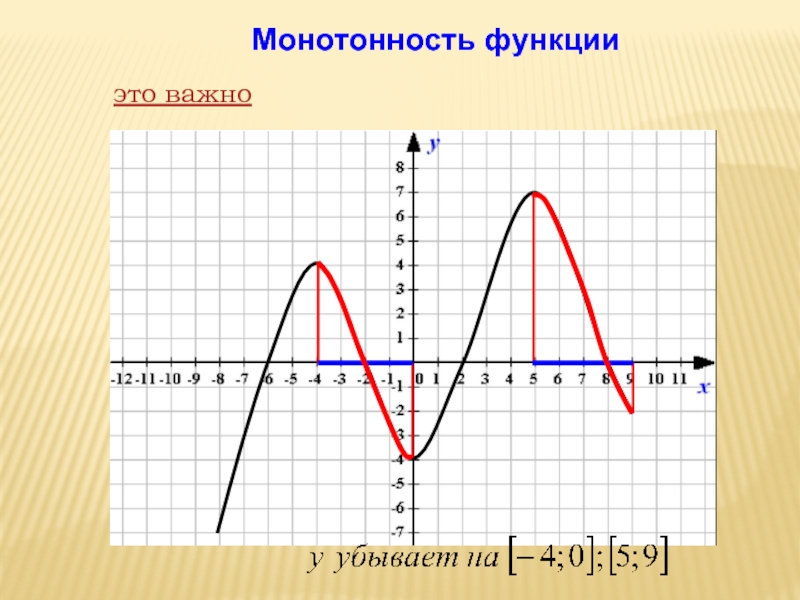
13. Монотонность функцииэто важно
14. Точки экстремума функцииэто важно
15. Скачать презентанцию

Дидактические принципы

Главная
Математика
Активные и интерактивные методы обучения как способы активизации учебно-познавательной деятельности учащихся на уроках математики.

Слайды и текст этой презентации

Слайд 1Современный урок математики с применением интерактивных средств обучения.
Г. Калязин, 2014
Выполнила:

преподаватель математики Старикова Наталия Валерьевна
ГБОУ СПО Калязинский колледж им. Н.М.

Полежаева

Современный урок математики с применением интерактивных средств обучения.Г. Калязин, 2014Выполнила: преподаватель математики Старикова Наталия ВалерьевнаГБОУ СПО Калязинский

Слайд 2Дидактические принципы

Слайд 3 Наша память запоминает

¼ - услышанного

1/3 – увиденного

½ - услышанного

и увиденного

¾ - при активном действии

Наша память запоминает ¼ - услышанного1/3 –

Слайд 4 Современный учитель в своей профессиональной образовательной деятельности использует

различные средства обучения. Среди технических новинок, особое место занимают интерактивные

доски – комплекс оборудования, позволяющий педагогу сделать процесс обучения ярким, наглядным, динамичным.

Современный учитель в своей профессиональной образовательной деятельности использует различные средства обучения. Среди технических новинок, особое

Слайд 5 Интерактивную доску можно применять на всех этапах урока:

при объяснении и закреплении нового материала, повторении и проверке его

усвоения, проверке домашнего задания и контроле.

Интерактивную доску можно применять на всех этапах урока: при объяснении и закреплении нового материала, повторении

Слайд 6При изучении новой темы можно использовать презентации, видеоматериалы, фотографии.

Слайд 7ОПРЕДЕЛЕНИЕ
3-угольник +
3 3-угольника
4-угольник +
4 3-угольника
6-угольник +
10-угольник +
n-угольник +
Пирамида

– это многогранник,
составленный из
n-угольника и
n треугольников.
6

3-угольников

10 3-угольников

n 3-угольников

Название пирамиды
определяет n-угольник

ОПРЕДЕЛЕНИЕ3-угольник + 3 3-угольника4-угольник + 4 3-угольника6-угольник +10-угольник +n-угольник +Пирамида – это многогранник, составленный из n-угольника

Слайд 8ПРОВЕРЬ СЕБЯ
Высота -
A
B
C
P
H
Основание -
ABC
многоугольник.
Боковые грани -
треугольники.
AP, BP, CP
Боковые

ребра -
.
Вершина -

общая точка всех
боковых граней.

отрезки,
соединяющие вершину с
вершинами основания.

ABP, BCP, ACP

перпендикуляр,
проведенный из вершины к плоскости основания.

ПРОВЕРЬ СЕБЯВысота - ABCP HОснование -ABCмногоугольник.Боковые грани -треугольники.AP, BP, CPБоковые ребра -.Вершина -

Слайд 91. Сколько боковых рёбер у пятиугольной пирамиды?
неверно
4
6
5
правильно
неверно
2.

Сколько граней у шестиугольной пирамиды?
3. У какой пирамиды за основание

можно взять боковую грань?

4. Какое наименьшее количество граней может быть у пирамиды?

5. Какое наименьшее количество ребер может быть у пирамиды?

6. Какая фигура является боковой гранью пирамиды?

неверно

трапеция

квадрат

треугольник

правильно

неверно

правильно

неверно

у любой

таких нет

у треугольной

правильно

неверно

правильно

неверно

правильно

неверно

Щелчком мыши выберите предполагаемый ответ
После выполнения заданий проведите анализ ваших ответов

тренажер «Проверь себя …»

1. Сколько боковых рёбер у пятиугольной пирамиды?неверно 4 6 5правильноневерно2. Сколько граней у шестиугольной пирамиды?3. У какой

Слайд 10Работа устно:
Н
Е
П
Р
Е

Слайд 11В некотором царстве, в некотором государстве пошёл Иван-царевич Василису- прекрасную

спасать.
От Кикиморы до Бабы-Яги три дорожки ведут, а от Бабы-Яги

до Кощея две.

Сколько вариантов есть у Ивана-царевича, чтобы дойти до Кощея?

Ответ:6

В некотором царстве, в некотором государстве пошёл Иван-царевич Василису- прекрасную спасать.От Кикиморы до Бабы-Яги три дорожки ведут,

Слайд 12D(y)=(-∞;+∞)
E(y)=(2;+∞)
0
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
x
y=3 -2
x
y=3 +2
x
y=3
x
Сдвиг y=3 +2 вдоль оси
OY вверх на

2 единицы
D(y)=(-∞;+∞)
E(y)=(-2;+∞)
x
Сдвиг y=3 -2 вдоль оси
OY вниз на 2

единицы

Преобразование графика функции y=a

Слайд 13 Монотонность функции
это важно

Слайд 14Точки экстремума функции
это важно

Скачать презентацию

Разделы презентаций

Активные и интерактивные методы обучения как способы активизации учебно-познавательной деятельности учащихся на уроках математики.

Содержание

Слайды и текст этой презентации

Слайд 1Современный урок математики с применением интерактивных средств обучения.
Г. Калязин, 2014
Выполнила:

преподаватель математики Старикова Наталия Валерьевна
ГБОУ СПО Калязинский колледж им. Н.М.

Слайд 2Дидактические принципы

Слайд 3 Наша память запоминает

¼ - услышанного

1/3 – увиденного

½ - услышанного

Слайд 4 Современный учитель в своей профессиональной образовательной деятельности использует

различные средства обучения. Среди технических новинок, особое место занимают интерактивные

Слайд 5 Интерактивную доску можно применять на всех этапах урока:

при объяснении и закреплении нового материала, повторении и проверке его

Слайд 6При изучении новой темы можно использовать презентации, видеоматериалы, фотографии.

Слайд 7ОПРЕДЕЛЕНИЕ
3-угольник +
3 3-угольника
4-угольник +
4 3-угольника
6-угольник +
10-угольник +
n-угольник +
Пирамида

– это многогранник,
составленный из
n-угольника и
n треугольников.
6

Слайд 8ПРОВЕРЬ СЕБЯ
Высота -
A
B
C
P
H
Основание -
ABC
многоугольник.
Боковые грани -
треугольники.
AP, BP, CP
Боковые

ребра -
.
Вершина -

Слайд 91. Сколько боковых рёбер у пятиугольной пирамиды?
неверно
4
6
5
правильно
неверно
2.

Сколько граней у шестиугольной пирамиды?
3. У какой пирамиды за основание

Слайд 10Работа устно:
Н
Е
П
Р
Е

Слайд 11В некотором царстве, в некотором государстве пошёл Иван-царевич Василису- прекрасную

спасать.
От Кикиморы до Бабы-Яги три дорожки ведут, а от Бабы-Яги

Слайд 12D(y)=(-∞;+∞)
E(y)=(2;+∞)
0
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
x
y=3 -2
x
y=3 +2
x
y=3
x
Сдвиг y=3 +2 вдоль оси
OY вверх на

2 единицы
D(y)=(-∞;+∞)
E(y)=(-2;+∞)
x
Сдвиг y=3 -2 вдоль оси
OY вниз на 2

Слайд 13 Монотонность функции
это важно

Слайд 14Точки экстремума функции
это важно

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Активные и интерактивные методы обучения как способы активизации учебно-познавательной деятельности учащихся на уроках математики.

Содержание

Слайды и текст этой презентации

Слайд 1Современный урок математики с применением интерактивных средств обучения.Г. Калязин, 2014Выполнила:

преподаватель математики Старикова Наталия ВалерьевнаГБОУ СПО Калязинский колледж им. Н.М.

Слайд 2Дидактические принципы

Слайд 3 Наша память запоминает

¼ - услышанного1/3 – увиденного½ - услышанного

Слайд 4 Современный учитель в своей профессиональной образовательной деятельности использует

различные средства обучения. Среди технических новинок, особое место занимают интерактивные

Слайд 5 Интерактивную доску можно применять на всех этапах урока:

при объяснении и закреплении нового материала, повторении и проверке его

Слайд 6При изучении новой темы можно использовать презентации, видеоматериалы, фотографии.

Слайд 7ОПРЕДЕЛЕНИЕ3-угольник + 3 3-угольника4-угольник + 4 3-угольника6-угольник +10-угольник +n-угольник +Пирамида

– это многогранник, составленный из n-угольника и n треугольников.6

Слайд 8ПРОВЕРЬ СЕБЯВысота - ABCP HОснование -ABCмногоугольник.Боковые грани -треугольники.AP, BP, CPБоковые

ребра -.Вершина -

Слайд 91. Сколько боковых рёбер у пятиугольной пирамиды?неверно 4 6 5правильноневерно2.

Сколько граней у шестиугольной пирамиды?3. У какой пирамиды за основание

Слайд 10Работа устно:НЕПРЕ

Слайд 11В некотором царстве, в некотором государстве пошёл Иван-царевич Василису- прекрасную

спасать.От Кикиморы до Бабы-Яги три дорожки ведут, а от Бабы-Яги

Слайд 12D(y)=(-∞;+∞)E(y)=(2;+∞) 012345-1-2-3-4-5-1-2-3-4-51234567891011xy=3 -2xy=3 +2xy=3xСдвиг y=3 +2 вдоль осиOY вверх на

2 единицыD(y)=(-∞;+∞)E(y)=(-2;+∞) xСдвиг y=3 -2 вдоль осиOY вниз на 2

Слайд 13 Монотонность функцииэто важно

Слайд 14Точки экстремума функцииэто важно

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Современный урок математики с применением интерактивных средств обучения.
Г. Калязин, 2014
Выполнила:

преподаватель математики Старикова Наталия Валерьевна
ГБОУ СПО Калязинский колледж им. Н.М.

¼ - услышанного

1/3 – увиденного

½ - услышанного

Слайд 7ОПРЕДЕЛЕНИЕ
3-угольник +
3 3-угольника
4-угольник +
4 3-угольника
6-угольник +
10-угольник +
n-угольник +
Пирамида

– это многогранник,
составленный из
n-угольника и
n треугольников.
6

Слайд 8ПРОВЕРЬ СЕБЯ
Высота -
A
B
C
P
H
Основание -
ABC
многоугольник.
Боковые грани -
треугольники.
AP, BP, CP
Боковые

ребра -
.
Вершина -

Слайд 91. Сколько боковых рёбер у пятиугольной пирамиды?
неверно
4
6
5
правильно
неверно
2.

Сколько граней у шестиугольной пирамиды?
3. У какой пирамиды за основание

Слайд 10Работа устно:
Н
Е
П
Р
Е

спасать.
От Кикиморы до Бабы-Яги три дорожки ведут, а от Бабы-Яги

Слайд 12D(y)=(-∞;+∞)
E(y)=(2;+∞)
0
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10
11
x
y=3 -2
x
y=3 +2
x
y=3
x
Сдвиг y=3 +2 вдоль оси
OY вверх на

2 единицы
D(y)=(-∞;+∞)
E(y)=(-2;+∞)
x
Сдвиг y=3 -2 вдоль оси
OY вниз на 2

Слайд 13 Монотонность функции
это важно

Слайд 14Точки экстремума функции
это важно