Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аркфункции.
Содержание
- 1. Аркфункции.
- 2. Обратная функция и её график.Сравним две функции
- 3. Вторая функция этим свойством не обладает.Например, для
- 4. Определение обратимой функции.Если функция y=f (x) такова,
- 5. Графики взаимно обратных функций.Если точка (х; у)
- 6. График функции y=arcsin x.Функция y=sin x возрастает
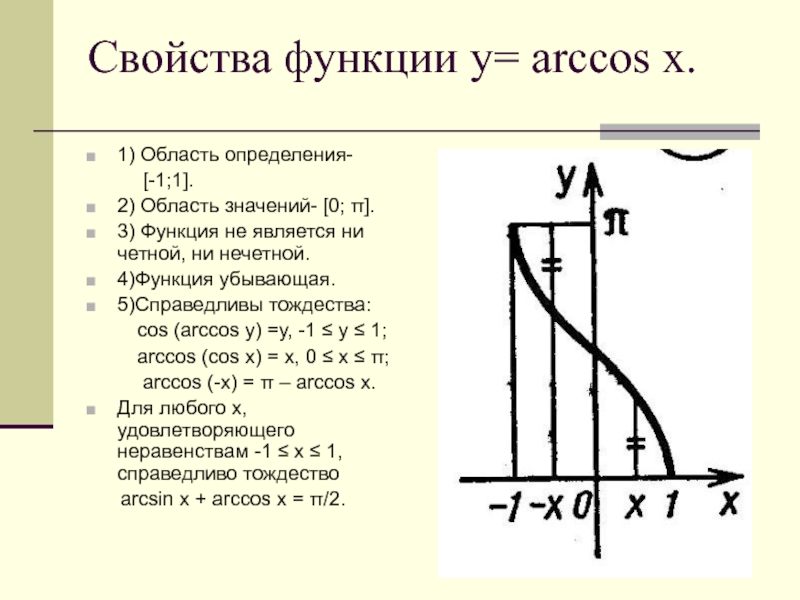
- 7. Свойства функции y = arcsin x.1)Область определения-
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Скачать презентанцию
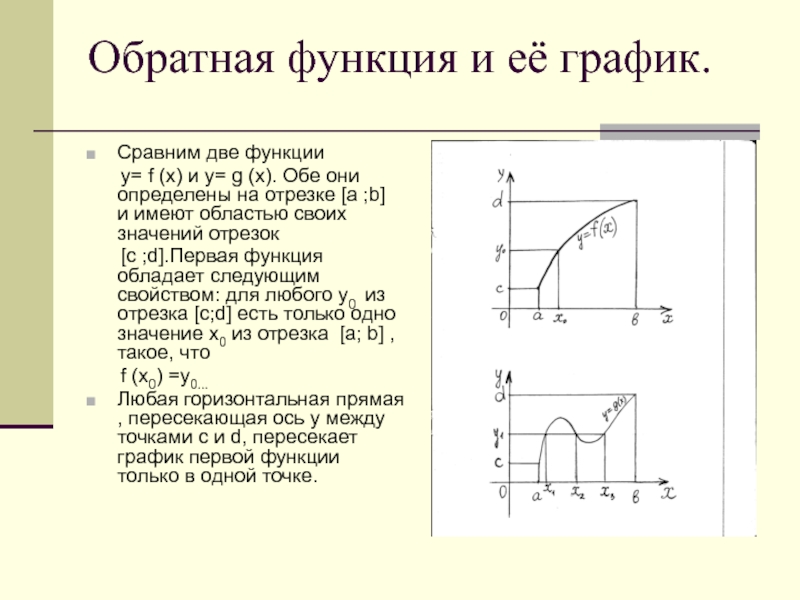
Обратная функция и её график.Сравним две функции y= f (x) и y= g (x). Обе они определены на отрезке [a ;b] и имеют областью своих значений отрезок
Слайды и текст этой презентации
Слайд 1Обратные тригонометрические функции.
1.Обратная функция. График обратной функции.
2.Свойства и графики обратных
тригонометрических функций.
Слайд 2Обратная функция и её график.
Сравним две функции
y= f (x) и y= g (x). Обе они определены
на отрезке [a ;b] и имеют областью своих значений отрезок[c ;d].Первая функция обладает следующим свойством: для любого y0 из отрезка [с;d] есть только одно значение x0 из отрезка [a; b] , такое, что
f (x0) =y0...
Любая горизонтальная прямая , пересекающая ось у между точками c и d, пересекает график первой функции только в одной точке.
Слайд 3Вторая функция этим свойством не обладает.
Например, для значения y1 прямая
y=y1 пересекает график функции
y= g (x)
в трех точках.Значит, в первом случае при каждом фиксированном y0 из отрезка [c;d] уравнение
f (x)=y0 имеет только один корень х0, а во втором случае при некоторых у, например, при у=у1 уравнение g (x)=y1 имеет более одного корня.
Слайд 4Определение обратимой функции.
Если функция y=f (x) такова, что для любого
её значения у0 уравнение f (x)=y0 имеет относительно х единственный
корень, то говорят, что функция f обратима.Если функция y=f (x) обратима, то, выразив х из формулы y=f (x) и поменяв затем х и у местами, получим обратную функцию.
Если функция y=f (x) определена и возрастает
( или убывает) на промежутке X и областью её значений является промежуток Y, то у неё существует обратная функция, причём обратная функция определена и возрастает (или убывает) на Y.
Пример. Доказать, что у функции у=2х-1 есть обратная, и найти её.
Решение. Функция у=2х-1 возрастает на всей числовой прямой, значит, у неё есть обратная функция. Выразим х:
х=0,5 (у+1).Поменяем х и у местами : у=0,5(х+1). Это и есть искомая обратная функция.
Слайд 5Графики взаимно обратных функций.
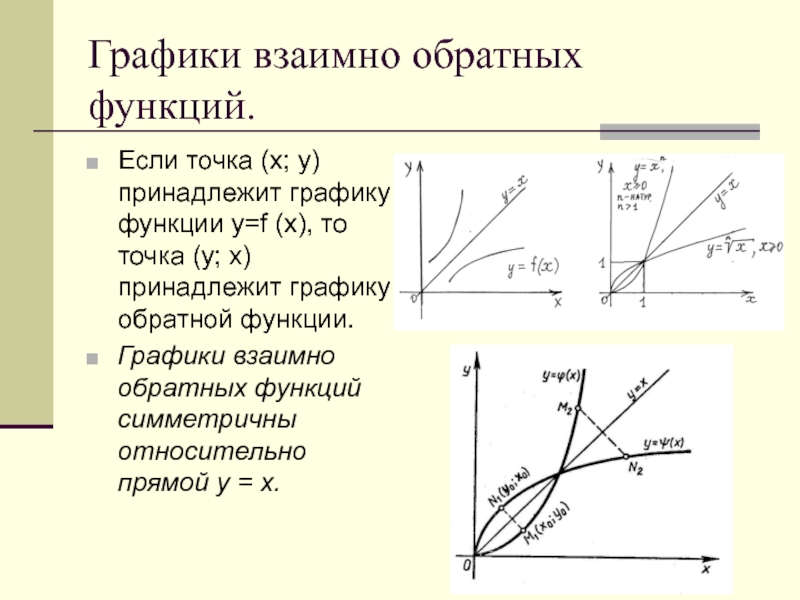
Если точка (х; у) принадлежит графику функции
y=f (x), то точка (у; х) принадлежит графику обратной функции.
Графики взаимно обратных функций симметричны относительно прямой у = х.
Слайд 6График функции y=arcsin x.
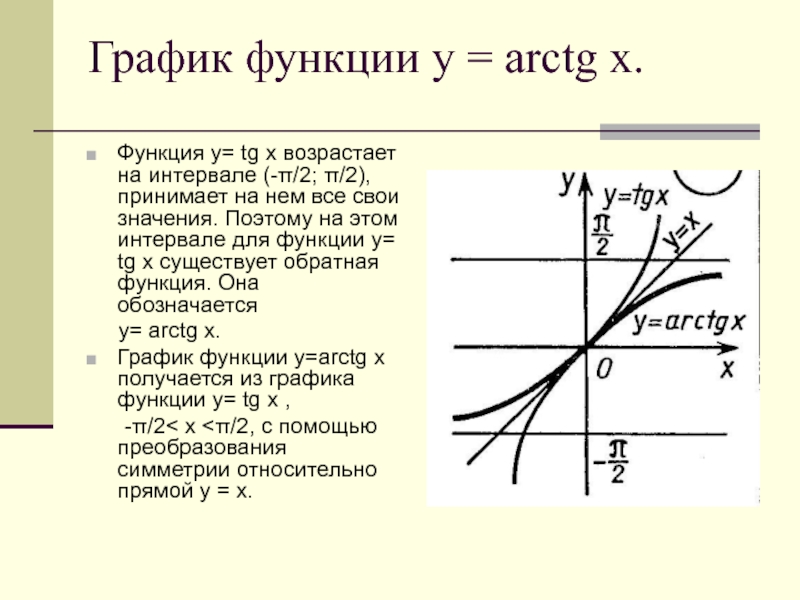
Функция y=sin x возрастает на [-π/2;π/2], и
принимает на нем все свои значения от -1 до 1.
Значит, для функции y=sin x,- π/2 ≤ x ≤ π/2, существует обратная функция
y= arcsin x.
График функции y= arcsin x может быть получен из графика функции y=sin x,
-π/2 ≤ х ≤ π/2, с помощью преобразования симметрии последнего относительно прямой у = х.
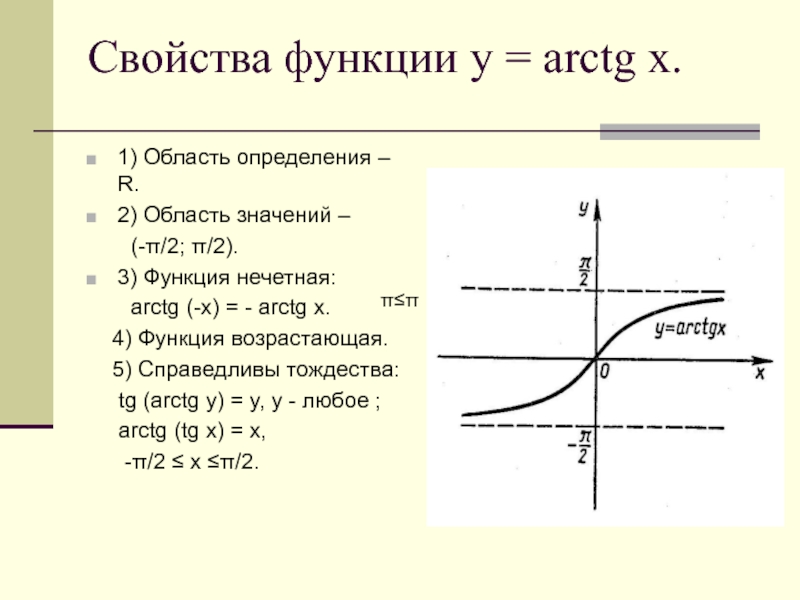
Слайд 7Свойства функции y = arcsin x.
1)Область определения-
[-1;1].
2) Область значений-
[-π/2; π/2].
3)Функция нечетная:
arcsin (-x)=-arcsin (x).4)Функция возрастающая.
5)Справедливы тождества:
sin (arcsin y)=y, -1≤y≤1;
arcsin (sin x)=x, -π/2 ≤ x ≤ π/2.



![Аркфункции. График функции y=arcsin x.Функция y=sin x возрастает на [-π/2;π/2], и принимает График функции y=arcsin x.Функция y=sin x возрастает на [-π/2;π/2], и принимает на нем все свои значения от](/img/thumbs/6a76caaf65dd64d03ce08ad0ce4bd886-800x.jpg)
![Аркфункции. Свойства функции y = arcsin x.1)Область определения- [-1;1].2) Область значений- Свойства функции y = arcsin x.1)Область определения- [-1;1].2) Область значений- [-π/2; π/2]. 3)Функция](/img/thumbs/f1db2363ab6cb57f4ba2ad2a607e38cf-800x.jpg)