Быстрое преобразование Фурье

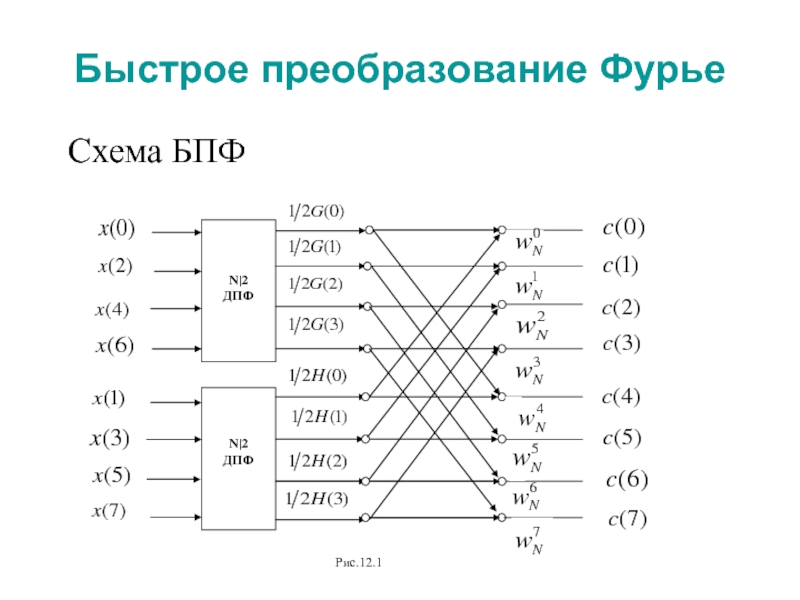
сигнала непосредственно по формуле ДПФ требует комплексных

умножений и комплексных сложений. Так как количество вычислений, а следовательно, и время вычислений приблизительно пропорциональны , то при больших количество арифметических операций весьма велико. Поэтому нахождение спектра в реальном времени даже для современной вычислительной техники представляет сложную задачу.
По этой причине представляет значительный интерес вычислительные процедуры, уменьшающие количество умножений и сложений.

операций вычисления ДПФ сигнала длины на вычисление преобразований Фурье с

меньшим числом точек. Разделив анализируемый набор отсчетов на части, вычисляют их ДПФ и объединяют результаты. Такие процедуры получили название алгоритмов быстрого преобразования Фурье БПФ.
При реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления последовательности отсчетов на части (прореживание по времени или по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге (основание БПФ).

2, когда длина последовательности ,

где целое число.
БПФ с прореживанием по времени. Рассмотрим идею БПФ с прореживанием по времени на примере деления набора отсчетов пополам. Введя общепринятое в литературе обозначение для дискретных экспоненциальных функций:


Запишем ДПФ сигнала в виде:

-точечные последовательности, состоящие из отсчетов

с четными и нечетными номерами соответственно. В результате получим:



Заменяя индексы суммирования на при четном и на
при нечетном , придем к выражению:

, то предыдущее выражение можно записать в виде:

(12.1)

Каждая из сумм (12.1) является точечным ДПФ: первая – для четных отсчетов исходной последовательности, а вторая – для нечетных. Несмотря на то, что индекс в формуле (12.1) распространяется на значений , каждая из сумм требует вычислений только для , так как и
периодичны по с периодом . Объединение же этих сумм приводит к точечному ДПФ .

точечное ДПФ разбиением сумм на два

точечных ДПФ. Таким образом, и могут быть вычислены в виде:

меньшей размерности, пока не останутся только двухточечные преобразования. Двухточечные ДПФ

(их число равно ) могут быть вообще вычислены без использования операций умножения. Действительно, для двухточечной последовательности согласно определению ДПФ имеем два спектральных отсчета:

сложение» можно оценить как

. Таким образом, вычислительные затраты по сравнению с непосредственным использованием формулы ДПФ уменьшается в раз. При больших это отношение становится весьма велико. Например, при
достигается более чем 100-кратное ускорение, но и это еще не предел. Количество комплексных умножений в алгоритме БПФ с прореживанием по времени может быть сокращено вдвое.

вычислений происходит преобразование одного множества из комплексных

чисел в другое множество из комплексных чисел.
Будем считать входным массивом на ступени вычисления , а – выходным массивом на ступени вычислений.
С учетом введенных обозначений имеем:

вдвое. Так как

, эти соотношения можно записать в виде:



Так как на каждую ступень разбиения имеется
таких операций, а общее число ступеней равно , то общее число пар операций «умножение-сложение» сокращается до .