Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дело о делимости
Содержание
- 1. Дело о делимости
- 2. Цель моей исследовательской работы: выявить
- 3. Гипотеза: Я предполагаю, что существует универсальный признак
- 4. Предмет исследования: Признак Паскаля. Методы исследования:
- 5. Признаки делимости - правило, позволяющее сравнительно быстро
- 6. Слайд 6
- 7. Слайд 7
- 8. ПРИЗНАК ДЕЛИМОСТИ НА 3: Натуральное число делится на
- 9. ПРИЗНАК ДЕЛИМОСТИ НА 10: Натуральное число делится на
- 10. Признак делимости на 5Если запись натурального числа
- 11. ПРИЗНАК ДЕЛИМОСТИ НА 9: Натуральное число делится на
- 12. ПРИЗНАК ДЕЛИМОСТИ НА 4: Натуральное число делится на
- 13. ПРИЗНАК ДЕЛИМОСТИ НА 6: Натуральное число делится на
- 14. ПРИЗНАК ДЕЛИМОСТИ НА 8: Натуральное число делится на
- 15. ДРУГИЕ ПРИЗНАКИ ДЕЛИМОСТИ, СЛЕДУЮЩИЕ ИЗ ДВУХ ПРИЗНАКОВПризнак
- 16. ВЫДАЮЩИЕСЯ МАТЕМАТИКИ, ЗАНИМАЮЩИЕСЯ ПРИЗНАКАМИ ДЕЛИМОСТИ. Леонардо
- 17. БЛЕЗ ПАСКАЛЬ
- 18. Иезуиты были врагами янсенистов, и в связи
- 19. ПРИЗНАК ПАСКАЛЯ: Натуральное число а
- 20. ПРИМЕНЕНИЕ ПРИЗНАКА
- 21. 6 – остаток от деления 1000
- 22. Следовательно, признак делимости на 7 можно сформулировать
- 23. Пример. Делится ли число 849756 на 7?
- 24. Выводы В ходе исследовательской работы я:
- 25. Заключение: Работая над
- 26. Спасибо за внимание!
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Цель моей исследовательской работы:
выявить и изучить универсальный
признак делимости.
Задачи:
● Найти и познакомиться с различными источниками информации по
данной теме.
● Систематизировать полученную информацию.
● Научиться с помощью универсального признака определять делимость чисел и формулировать признаки делимости на любое число.
Цели и задачи
Слайд 3Гипотеза:
Я предполагаю, что существует универсальный признак делимости.
В результате изучения
различной литературы, моя гипотеза была подтверждена.
Слайд 4Предмет исследования:
Признак Паскаля.
Методы исследования:
● Изучение литературы и электронных источников.
● Систематизация и обобщение полученной информации.
● Применение изученной теории
при решении проблемных задач.Слайд 5
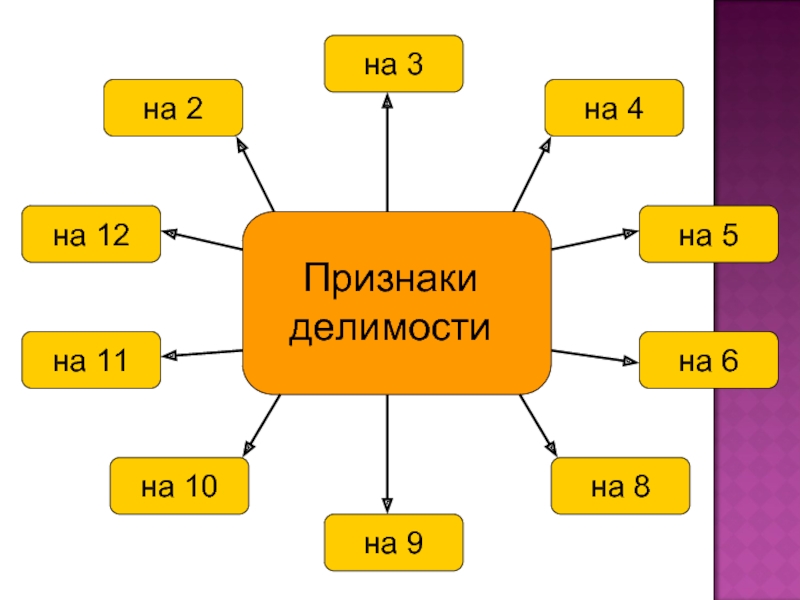
Признаки делимости - правило, позволяющее сравнительно быстро определить, является ли
число кратным заранее заданному без необходимости выполнять фактическое деление.
Слайд 8ПРИЗНАК ДЕЛИМОСТИ НА 3:
Натуральное число делится на 3 тогда и
только тогда, когда сумма его цифр делится на 3.
Например: число
12 345 делится на 3, т.к. 1+2+3+4+5=15, а 15 делится на 3, а число 3 490 не делится на 3, т.к. 3+4+9+0=16, а 16 не делится на 3.Слайд 9ПРИЗНАК ДЕЛИМОСТИ НА 10:
Натуральное число делится на 10 тогда и
только тогда, когда оно оканчивается на 0.
Например: число 20 800
делится на 10, а число 45 687 не делится на 10.Слайд 10Признак делимости на 5
Если запись натурального числа оканчивается 0 или
5, то это число делится на 5.
Слайд 11ПРИЗНАК ДЕЛИМОСТИ НА 9:
Натуральное число делится на 9 тогда и
только тогда, когда сумма его цифр делится на 9.
Например: число
45 981 делится на 9,т.к. 4+5+9+8+1=27, а 27 делится на 9, а число 7 734 не делится на 9, т.к. 7+7+3+4=21,а 21 не делится на 9. Слайд 12ПРИЗНАК ДЕЛИМОСТИ НА 4:
Натуральное число делится на 4 тогда и
только тогда, когда последние две его цифры образуют число, делящееся
на 4.Слайд 13ПРИЗНАК ДЕЛИМОСТИ НА 6:
Натуральное число делится на 6 тогда и
только тогда, когда оно делится на 2 и на 3
одновременно.Например: число 3 576 делится на 6, т.к. оно делится на 2 и на 3, а число 89 331 не делится на 6, т.к. оно делится на 3, но не делится на 2.
Слайд 14ПРИЗНАК ДЕЛИМОСТИ НА 8:
Натуральное число делится на 8 тогда и
только тогда, когда последние три его цифры образуют число, делящееся
на 8.Например: число 812 672 делится на 8, т.к. 72 делится на 8, а число 723 не делится на 8, т.к. 23 не делится на 8.
Слайд 15ДРУГИЕ ПРИЗНАКИ ДЕЛИМОСТИ, СЛЕДУЮЩИЕ ИЗ ДВУХ ПРИЗНАКОВ
Признак делимости на 12.
Число делится на 12
оно делится
и на 3, и на 4. (589 524)Признак делимости на 14. Число делится на 14
оно делится и на 2, и на 7. (364)
Признак делимости на 15. Число делится на 15
оно делится и на 3, и на 5. (8 445)
Слайд 16ВЫДАЮЩИЕСЯ МАТЕМАТИКИ, ЗАНИМАЮЩИЕСЯ ПРИЗНАКАМИ ДЕЛИМОСТИ.
Леонардо Фибоначчи
Блез Паскаль
(1170 – 1228 г.г.) (1623 – 1662 г.г.)
Слайд 17 БЛЕЗ ПАСКАЛЬ
(1623 – 1662 Г.Г.)
Французский математик, физик, философ, писатель.
Родился в семье одного из лучших юристов города Клермон-Ферран. Отец, глубоко интересуясь математикой, привил любовь к этой науке своему сыну, который впоследствии стал одним из крупнейших математиков и физиков Франции.
Невероятные успехи Блеза до сих пор считают ярким проявлением таланта, граничащего с гениальностью.
Первый свой трактат по математике он написал в возрасте 17 лет. Далее его открытия последовали одно за другим. Однако успех не вскружил ему голову и к 30-летнему возрасту он глубоко погрузился в религию и философию.
Блез стал последователем янсенизма —учения, противоречащего ортодоксальному католицизму и отрицавшего свободу воли, признававшего предопределение и требовавшего от своих адептов аскетизма и бескомпромиссного этического самосовершенствования.
Слайд 18
Иезуиты были врагами янсенистов, и в связи с этим ученый
написал книгу «Письма к провинциалу» —шедевр сатирической прозы, который доказывает
полную несостоятельность иезуитских доктрин.Последние годы жизни Паскаль провел в монастыре Пор-Руаяль-д-Шан — интеллектуальном сердце столицы Франции.
После смерти вышел в свет его труд «Мысли», который был издан близкими друзьями и почитателями. В «Мыслях» Паскаль развивает представление о трагичности и хрупкости человека, находящегося между двумя безднами — бесконечностью и ничтожеством (человек — «мыслящий тростник»).
Все, о чем писал Паскаль, было им глубоко пережито и выстрадано. О себе самом он говорил: «Я только с теми, кто стеная, ищет истину».
Слайд 19ПРИЗНАК ПАСКАЛЯ:
Натуральное число а разделится на другое
натуральное число b только в том случае, если сумма произведений
цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число.
Слайд 20 ПРИМЕНЕНИЕ ПРИЗНАКА ПАСКАЛЯ
Покажем теперь, как
с помощью этого универсального признака делимости, можно сформулировать признак делимости
на любое число, например на 7. 2814 :7Найдём остатки при делении 10, 100, 1000 на 7
Слайд 21
6 – остаток от деления 1000 на 7;
2
- остаток от деления 100 на 7,
3 -
остаток от деления 10 на 72814 делится на 7, т.к.
2·6 + 8 ·2 +1·3 +4 = 35,
35:7=5
Слайд 22
Следовательно, признак делимости на 7 можно сформулировать следующим образом:
Чтобы
проверить, делится ли число на 7, нужно найти остатки, полученные
при деление разрядных единиц этого числа на число 7. Затем найти сумму произведений цифр заданного числа и соответствующих остатков.Если результат будет делиться на 7, то и само число будет делиться на 7.
Слайд 23
Пример.
Делится ли число 849756 на 7?
Попробуем ответить на этот вопрос,
применяя признак Паскаля и зная остатки при делении на 7
от 10, 100, 1000, 10000… Число 6+3∙5+2∙7+6∙9+4∙4+5∙8 имеет такой же остаток как и 6+1+0+5+2+5=19, то есть 5. Число 849756 не делится на 7.Слайд 24Выводы В ходе исследовательской работы я: 1. Нашел и познакомился с различными
источниками информации по теме делимость чисел, универсальный признак делимости натуральных
чисел. 2. Систематизировала полученную информацию. 3. Научился пользоваться признаком Паскаля для определения делимости чисел, а также формулировать признаки делимости на любое натуральное число. Все это позволило более широко изучить тему делимости чисел, расширило мой математический кругозор, узнал, как работает универсальный признак Паскаля, как его можно применить при решении задач, познакомился с биографией замечательного математика Б.Паскаля.Получил навык работы с научной литературой, научился более точно и грамотно излагать свои мысли, делать выводы.