Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электронное учебно-методическое средство Презентация по теме Теорема Пифагора
Содержание
- 1. Электронное учебно-методическое средство Презентация по теме Теорема Пифагора
- 2. «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора»
- 3. ОБРАЗОВАТЕЛЬНЫЕ ЗАДАЧИ:Познакомить учащихся с доказательствами теоремы
- 4. ВОСПИТАТЕЛЬНЫЕ ЗАДАЧИ: Воспитывать: целостное отношение к окружающему
- 5. ТеоремаПифагора
- 6. О теореме Пифагора Пребудет вечной истина, как
- 7. Теорема ПифагораДоказательство:В прямоугольном треугольнике квадрат гипотенузы равен
- 8. Если дан нам треугольникИ притом с прямым
- 9. abc2 = a2 + b2a2 = c2 – b2b2 = c2 – a2Формулы:с
- 10. Алгоритм решения задач по теореме Пифагора Внимательно
- 11. Решение задачНайти неизвестную сторону треугольника
- 12. Устная работа1)Выдели на чертеже прямоугольный треугольник. Найди катеты и гипотенузу. Запиши теорему Пифагора
- 13. Выдели на чертеже прямоугольный треугольник. Найди катеты и гипотенузу. Запиши теорему Пифагора
- 14. Выдели на чертеже прямоугольный треугольник. Найди катеты и гипотенузу. Запиши теорему Пифагора
- 15. Сформулируйте утверждения, обратные данным:1) В равнобедренном
- 16. Теорема, обратная теореме Пифагора:Если квадрат одной стороны
- 17. Определите, является ли треугольник со сторонами13 м; 5 м; 12 м; прямоугольным? Решение:
- 18. Определите, является ли треугольник со сторонами
- 19. Древнерусская задачаСлучися некоему человеку к стене лествицу
- 20. Дано: Решение:
- 21. Тополь у реки«На берегу реки рос тополь
- 22. Дано: АС = 3 фута , AD = 4 фута, BC =СDНайти: АВ.Решение:
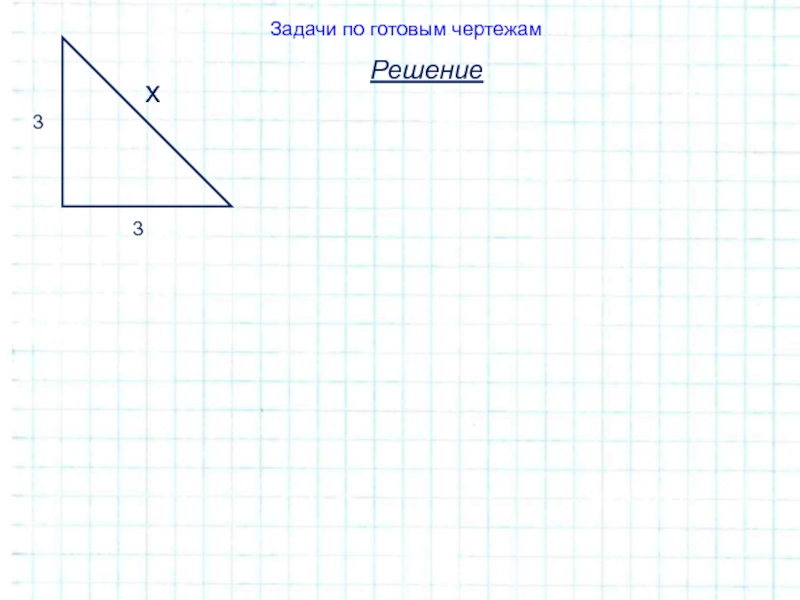
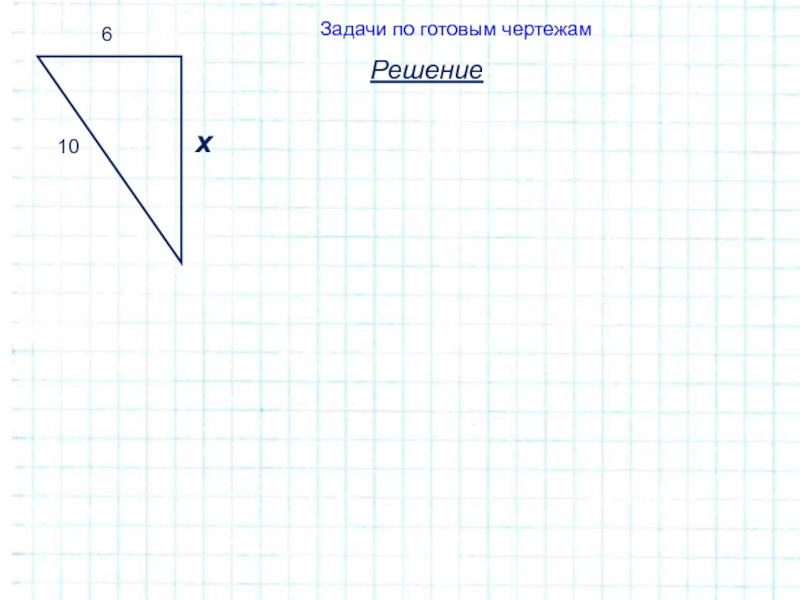
- 23. 3ччРешениеЗадачи по готовым чертежам
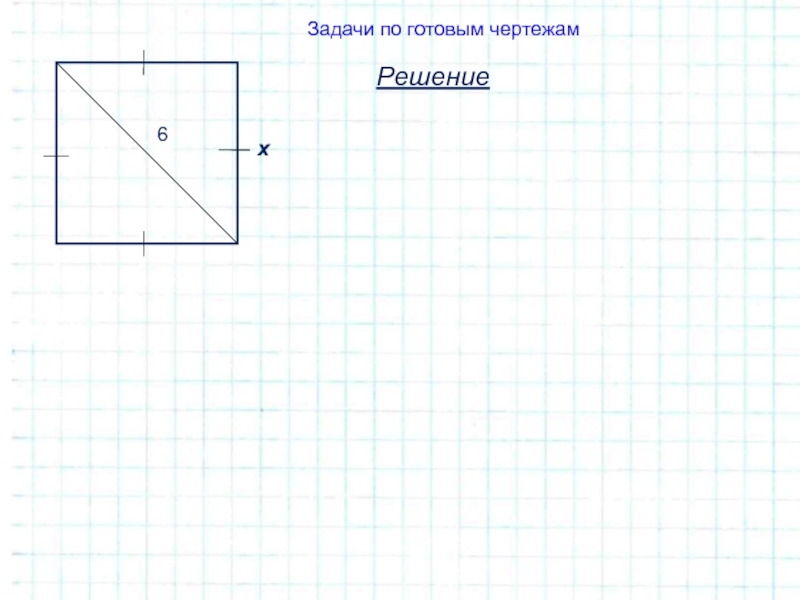
- 24. РешениеЗадачи по готовым чертежам
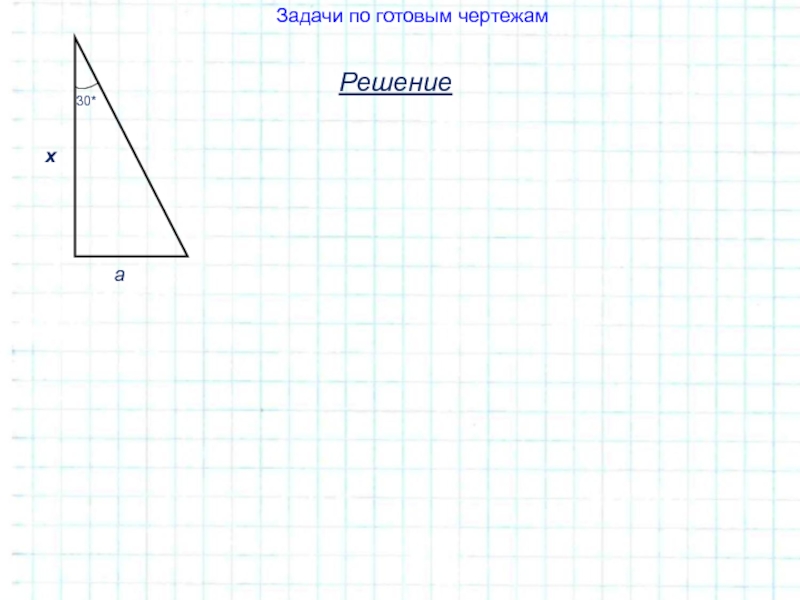
- 25. РешениеЗадачи по готовым чертежам
- 26. РешениеЗадачи по готовым чертежам
- 27. Меньшая сторона параллелограмма 8 см, периметр 36
- 28. Меньшая сторона параллелограмма 8 см, периметр 36
- 29. Меньшая сторона параллелограмма 8 см, периметр 36
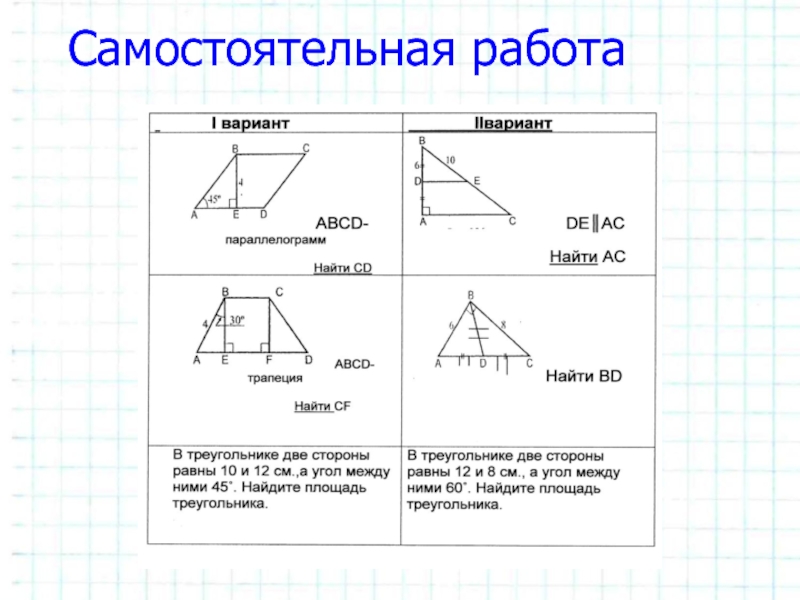
- 30. Самостоятельная работа
- 31. Слайд 31
- 32. Слайд 32
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Разработка урока по геометрии «Теорема Пифагора» учителя математики МБОУ СОШ
№7 г. Каменска-Уральского
Захаровой Светланы Закарьевны.
Слайд 3ОБРАЗОВАТЕЛЬНЫЕ ЗАДАЧИ:
Познакомить учащихся с доказательствами теоремы Пифагора, обратной теоремой.
Применять
теорему Пифагора к решению задач.
Привить навыки работы с интерактивной доской.
Слайд 4ВОСПИТАТЕЛЬНЫЕ ЗАДАЧИ:
Воспитывать:
целостное отношение к окружающему миру
посредством математики.
чувства
ответственности, самостоятельной
деятельности при самооценке результатов
работы с учебным материалом.
Слайд 6
О теореме Пифагора
Пребудет вечной истина, как скоро
Все познает слабый
человек! И ныне теорема Пифагора Верна, как и в его далекий век. Обильно
было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя, вслед. Они не в силах свету помешать, А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.A.Шамиссо
Слайд 7Теорема Пифагора
Доказательство:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Дано:
прямоугольный треугольник. с-гипотенуза, а,в-катеты.
Доказать:c2 = a2 + b2
Слайд 8Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы
всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким
простым путемК результату мы придем.
И. Дырченко
Слайд 10Алгоритм решения задач по теореме Пифагора
Внимательно прочти задачу, разберись
с условием.
По условию сделай чертеж.
Выдели на чертеже прямоугольный
треугольник. Найди катеты и гипотенузу.
Запиши теорему Пифагора и соотнеси данные в задаче с ней.
Выполни подстановку данных.
Соотнеси полученный ответ с вопросом задачи и смыслом условия.
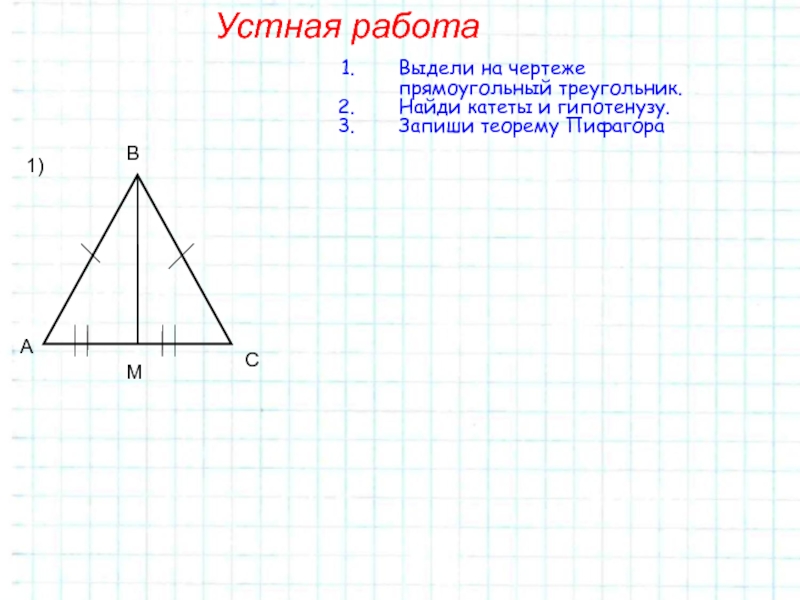
Слайд 12Устная работа
1)
Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши теорему Пифагора
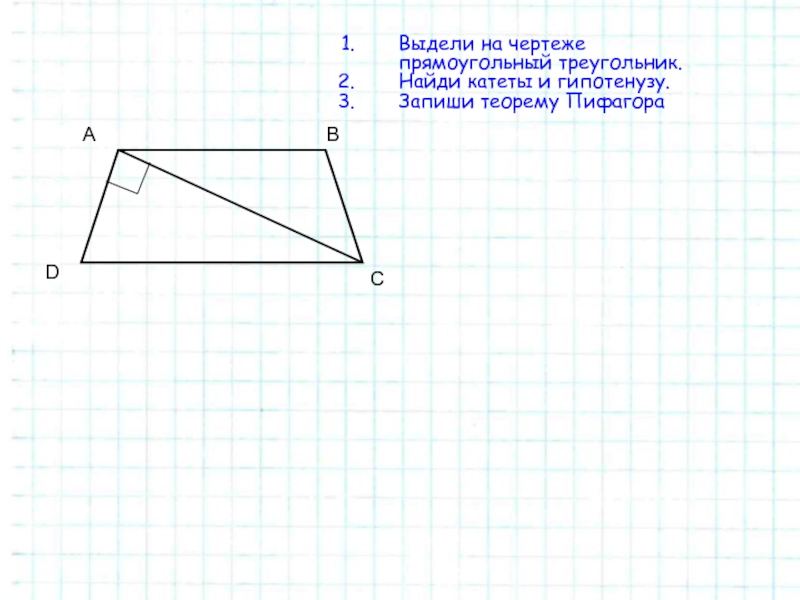
Слайд 13Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши
теорему Пифагора
Слайд 14Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши
теорему Пифагора
Слайд 15Сформулируйте утверждения, обратные данным:
1) В равнобедренном треугольнике углы при
основании равны.
Если в треугольнике углы при основании равны, то этот
треугольник равнобедренный2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если при пересечении двух прямых секущей, накрест лежащие углы равны, то эти прямые параллельны.
3) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то этот треугольник прямоугольный.
Слайд 16Теорема, обратная теореме Пифагора:
Если квадрат одной стороны треугольника равен сумме
квадратов двух других его сторон, то этот треугольник прямоугольный.
Слайд 18Определите, является ли треугольник со сторонами 0,6 дм; 0,8 дм;
1,2 дм прямоугольным?
Решение:
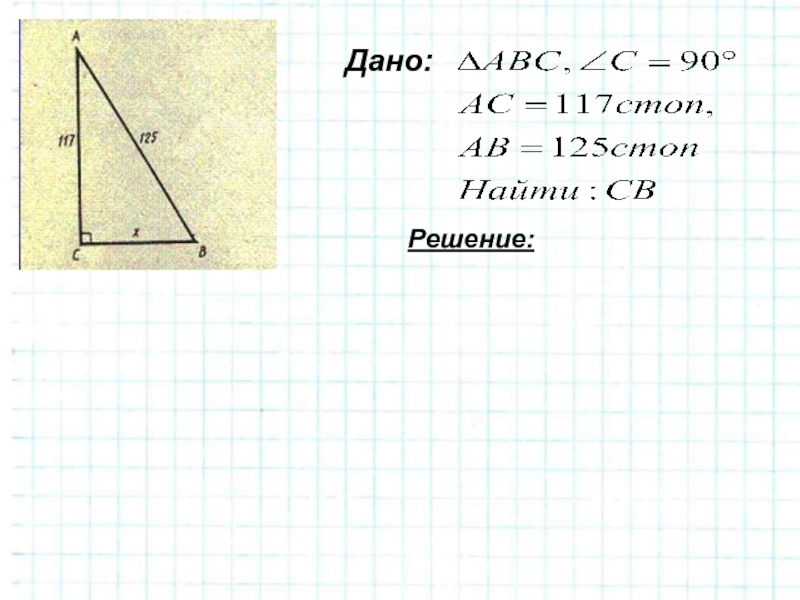
Слайд 19Древнерусская задача
Случися некоему человеку
к стене лествицу прибрати,
стены тоя
же высота
есть 117 стоп. И обрете лествицу
долготою 125
стоп. И ведати хощет, колико стоп сея лествици нижний конец
от стены отстояти имать?
Слайд 21Тополь у реки
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв
его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки
его угол составлял.Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Слайд 27Меньшая сторона параллелограмма 8 см, периметр 36 см. Одна из
диагоналей параллелограмма перпендикулярна боковой стороне. Найти площадь параллелограмма.
Решение:Слайд 28Меньшая сторона параллелограмма 8 см, периметр 36 см. Одна из
диагоналей параллелограмма перпендикулярна боковой стороне. Найти площадь параллелограмма.
Решение:Дано: ABCD- параллелограмм
AD=8см, Р=36см,BD ┴ AD
Найти: S ABCD
A
D
C
B
Решение:
Т.К. Р=36 см, AD=8см, то АВ=____см.
∆АВD- __________, _____--- гипотенуза, __,__- катеты, значит по т. Пифагора
S ABCD=S∆ABD+S∆DBC, т.к. S∆ABD=S∆DBC по двум катетам, то S ABCD=2∙S∆ABD,
S ABCD=2∙0,5∙6∙8=48 кв.см.
Ответ: 48
Слайд 29Меньшая сторона параллелограмма 8 см, периметр 36 см. Одна из
диагоналей параллелограмма перпендикулярна боковой стороне. Найти площадь параллелограмма.
Решение:Дано: ABCD- параллелограмм
AD=8см, Р=36см,BD ┴ AD
Найти: S ABCD
A
D
C
B
Решение:
Т.К. Р=36 см, AD=8см, то АВ=10см.
∆АВD- прямоугольный, АВ- гипотенуза, AD,BD- катеты, значит по т. Пифагора
S ABCD=S∆ABD+S∆DBC, т.к. S∆ABD=S∆DBC по двум катетам, то S ABCD=2∙S∆ABD,
S ABCD=2∙0,5∙6∙8=48 кв.см.
Ответ: 48