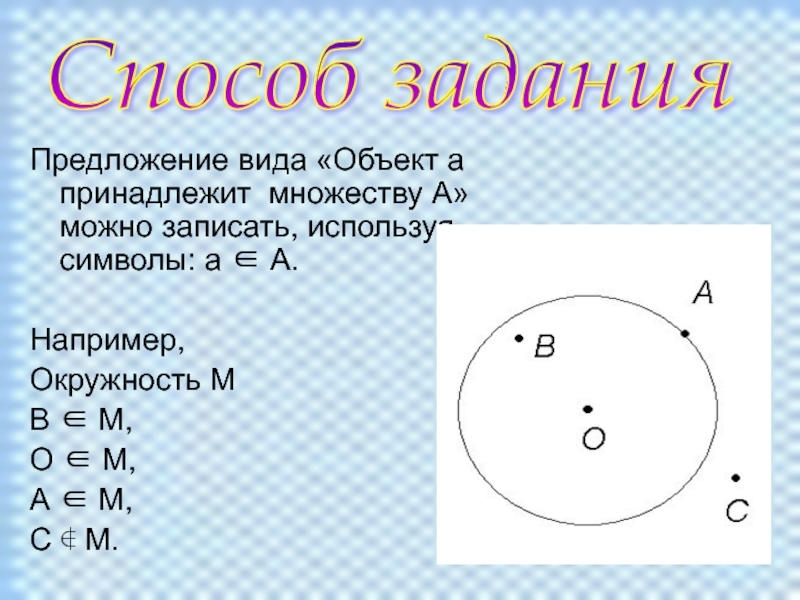
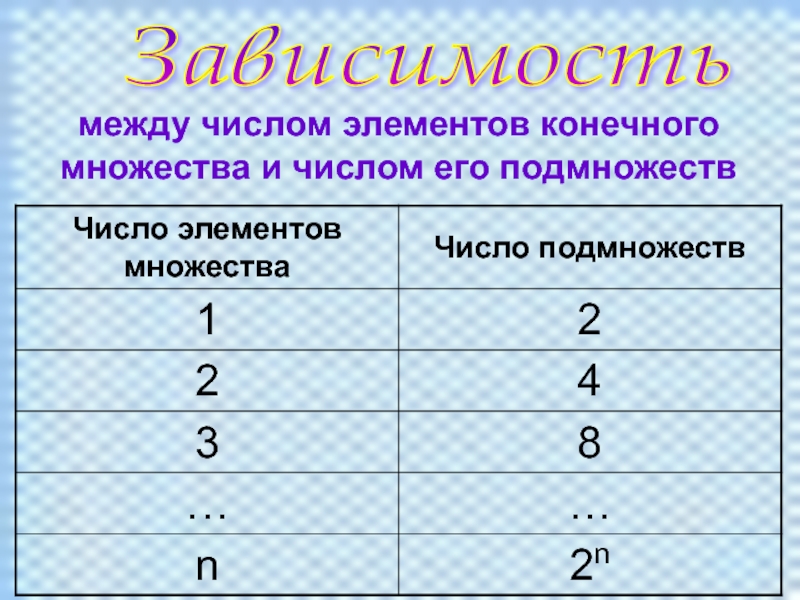
подмножеств данного множества;
Понятие универсального множества;
Равные множества.
3. Действия над множествами.
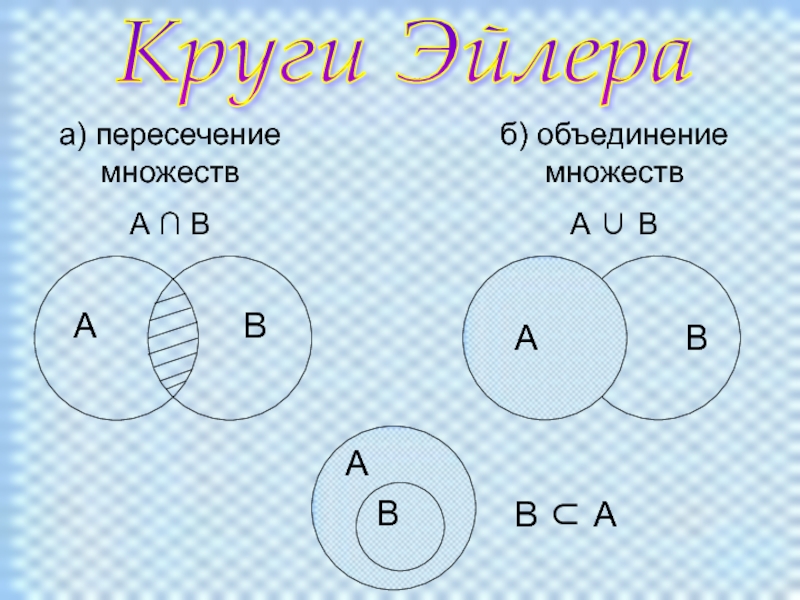
Пересечение;
Объединение;
Разность;
Дополнение.
4. Решение
задач с использованием кругов Эйлера.План