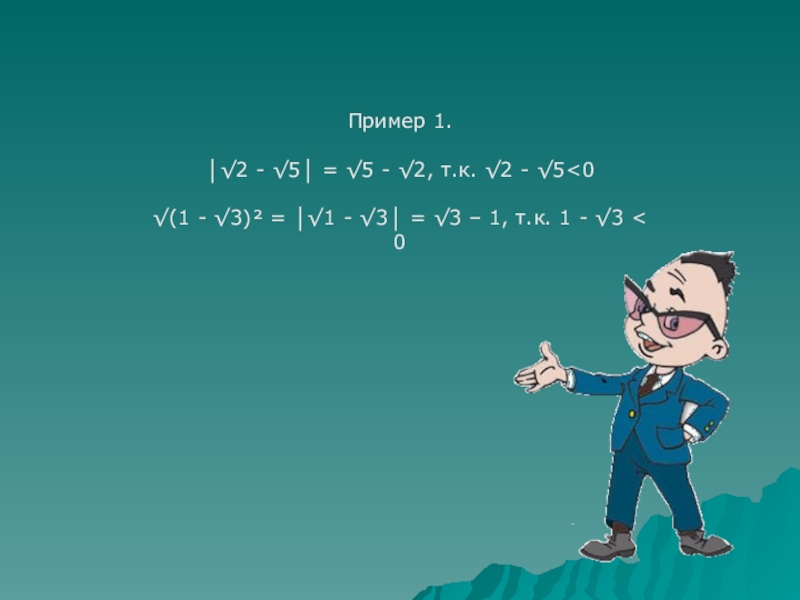Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интересный модуль
Содержание
- 1. Интересный модуль
- 2. Свойства модуля, изучаемые в школе МБОУ
- 3. 1. Определение модуля 2. Свойства модуля 3. Некоторые примеры применения модуля
- 4. Модулем числа а называют расстояние (в единичных
- 5. Модулем неотрицательного действительного числа a называют само
- 6. Модуль числа не может быть отрицательным. Для
- 7. На практике используют различные свойства модулей:|а| ≥ 0|а·b|
- 8. Пример 1.│√2 - √5│ = √5 - √2, т.к. √2 - √5
- 9. Пример 2.Упростить выражение , если a <
- 10. Для решения уравнений, содержащих знак абсолютной величины,
- 11. Пример 1.Решим аналитически и графически уравнение │х
- 12. Графическое решениеОдним из способов решения уравнений, содержащих
- 13. 2 способ. Ответ: х = - 1; 5
- 14. Графическое решение уравнения │х – 2 │=
- 15. Пример 2.Решим уравнение │х - 2│= 0х
- 16. Пример 3.Решим уравнение │х - 2│= -
- 17. Список литературы: 1.Виленкин Ю.Н. Математика 6 кл.
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Свойства модуля, изучаемые в школе МБОУ Кадряковская ООШ Агрызского
муниципального района
8 классаСлайд 4
Модулем числа а называют расстояние (в единичных отрезках) от начала
координат до точки А(а).
Модуль числа 5 равен 5 так как
точка В(5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5Расстояние точки М(-6) от начала отсчета О равно 6 единичным отрезкам. Число 6 называют модулем числа -6. Пишут: |-6| = 6
Слайд 5
Модулем неотрицательного действительного числа a называют само это число:
|а| =
а
Модулем отрицательного действительного числа х называют противоположное число:
|а| = -
аКороче это записывают так:
Слайд 6
Модуль числа не может быть отрицательным. Для положительного числа и
нуля он равен самому числу, а для отрицательного – противоположному
числу. Противоположные числа имеют равные модули:|-а| = |а|
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков:
|0| = 0
Слайд 7
На практике используют различные свойства модулей:
|а| ≥ 0
|а·b| = |а| ·
|b|
|а|n = аn , n є Z, a ≠ 0,
n > 0|а| = | - а|
|а + b| ≤ |а| + |b|
|а·q| = q·|а| , где q - положительное число
|а|2 = а2
Значение |a - b| равно расстоянию на числовой прямой между точками, изображающими числа a и b.
Слайд 9
Пример 2.
Упростить выражение
, если a < 0.
Решение.
Так как по
условию а < 0, то |а| = -а. В результате
получаемОтвет:
Слайд 10
Для решения уравнений, содержащих знак абсолютной величины,
мы будем основываться
на определении модуля числа и свойствах
абсолютной величины числа. Мы
решим несколько примеров одними тем же способом и посмотрим, какой из способов окажется проще
для решения уравнений, содержащих модуль.
Слайд 11
Пример 1.
Решим аналитически и графически уравнение │х - 2│ =
3
Если х – 2 > 0, то х – 2
= 3, х = 5Если х – 2 < 0, то х – 2 = - 3, х = - 1
Ответ: х = 5; - 1.
Вывод: если модуль некоторого выражения равен действительному
Положительному числу а, тогда выражение под модулем равно либо
а, либо – а.
Слайд 12
Графическое решение
Одним из способов решения уравнений, содержащих модуль является графический
способ. Суть этого способа заключается в том, чтобы построить графики
данных функций. В случае, если графики пересекутся, точки пересечений данных графиков будут являться корнями нашего уравнения. В случае, если графики не пересекутся, мы сможем сделать вывод, что уравнение корней не имеет. Этот способ, вероятно, реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.Другой способ решения уравнений, содержащих модуль- это способ разбиения числовой прямой на промежутки. В этом случае нам нужно разбить числовую прямую так, что по определению модуля, знак абсолютной величины на данных промежутках можно будет снять. Затем, для каждого из промежутков мы должны будем решить данное уравнение и сделать вывод, относительно получившихся корней(удовлетворяют они нашему промежутку или нет). Корни, удовлетворяющие промежутки и дадут окончательный ответ.
Слайд 14
Графическое решение уравнения │х – 2 │= 3
Для решения уравнения
графическим способом надо построить графики функций
у = │х –
2 │и у = 3.Прямая графика функции у = 3 пересеклась с графиком функции у = │х – 2 │ в точках с координатами (-1;3) и (5;3), следовательно решениями уравнения будут абсциссы точек
х = 5, х = -1
Ответ: х=5, х= -1
Слайд 15
Пример 2.
Решим уравнение │х - 2│= 0
х – 2 =0,
х = 2
Ответ: х = 2
Вывод: если модуль некоторого
выражения равен 0, тогда выражение под модулем равно 0.Слайд 16
Пример 3.
Решим уравнение │х - 2│= - 2
Это уравнение не
имеет корней, так как подкоренное выражение не может быть отрицательным
числом.Слайд 17
Список литературы: 1.Виленкин Ю.Н. Математика 6 кл. Москва. Мнемозина. 2009.
159 с. 2. Еженедельная учебно - методическая газета. Математика.Модуль -
это просто. 2007. №8 10-11с.5.Макарычев Ю.Н. Алгебра 7 кл. Москва. Просвещение 2009. 78-81 с.
3. Еженедельная учебно - методическая газета. Математика. Решение уравнений с модулями. 2004. №3. 9-13 с. 4. Алтынов Г.И. Краткий справочник школьника 5-11. Москва. Дрофа. 2005. 331с.