Логические операции

Содержание

1. Логические операции
2. — способ построения сложного высказывания из данных
3. - образуется из высказывания с помощью добавления
4. Истинность высказывания, имеющего форму Ā
5. Графическая иллюстрация инверсии с помощью диаграмм Эйлера
6. - образуется соединением двух высказываний в одно
7. Таблица истинности конъюнкции:МОУ СОШ №
8. Графическая иллюстрация конъюнкции с помощью диаграмм Эйлера
9. образуется соединением двух высказываний в одно с
10. Примеры строгих и нестрогих дизъюнкций:МОУ СОШ № 19 "Выбор" г. Находка
11. Под дизъюнкцией будем понимать нестрогую
12. Таблица истинности дизъюнкции:МОУ СОШ №
13. Графическая иллюстрация дизъюнкции с помощью диаграмм Эйлера
14. образуется соединением двух высказываний в одно с
15. Таблица истинности импликации:МОУ СОШ № 19 "Выбор"
16. Графическая иллюстрация импликации с помощью диаграмм Эйлера — Венна:(A=0)∩(B=0)(A=0)∩(B=1)(A=1)∩(B=1)МОУ СОШ № 19 "Выбор" г. НаходкаBА
17. образуется соединением двух высказываний в
18. Таблица истинности эквивалентности:МОУ СОШ №
19. Графическая иллюстрация эквивалентности с помощью диаграмм Эйлера — Венна:(A=0)∩(B=0)(A=1)∩(B=1)МОУ СОШ № 19 "Выбор" г. НаходкаBА
20. Лыскова В.Ю., Ракитина Е.А. Логика в информатике.Семакин
21. Скачать презентанцию

— способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.Истинное высказывание в логике обозначается - 1, ложное – 0Высказывания обозначаются буквами

Слайды и текст этой презентации

Слайд 1
Логическое отрицание (инверсия)
Логическое умножение (конъюнкция)
Логическое сложение (дизъюнкция)
Логическое следование (импликация)
Логическое равенство

(эквивалентность)

МОУ СОШ № 19 "Выбор" г. Находка
Логические операции

Логическое отрицание (инверсия)Логическое умножение (конъюнкция)Логическое сложение (дизъюнкция)Логическое следование (импликация)Логическое равенство (эквивалентность)МОУ СОШ № 19

Слайд 2— способ построения сложного высказывания из данных высказываний, при котором

значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

Истинное

высказывание в логике обозначается - 1, ложное – 0
Высказывания обозначаются буквами латинского алфавита: А, В, С и т.д.

МОУ СОШ № 19 "Выбор" г. Находка

Логическая операция

— способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями

Слайд 3- образуется из высказывания с помощью добавления частицы «не» к

сказуемому или использования оборота речи «неверно, что…».

Обозначение инверсии:
НЕ А;
¬ A;
Ā;
NOT

А.

МОУ СОШ № 19 "Выбор" г. Находка

Логическое отрицание (инверсия)

А = Дождя не будет
Ā = Неверно, что дождя не будет. (Дождь будет. )

- образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что…».Обозначение

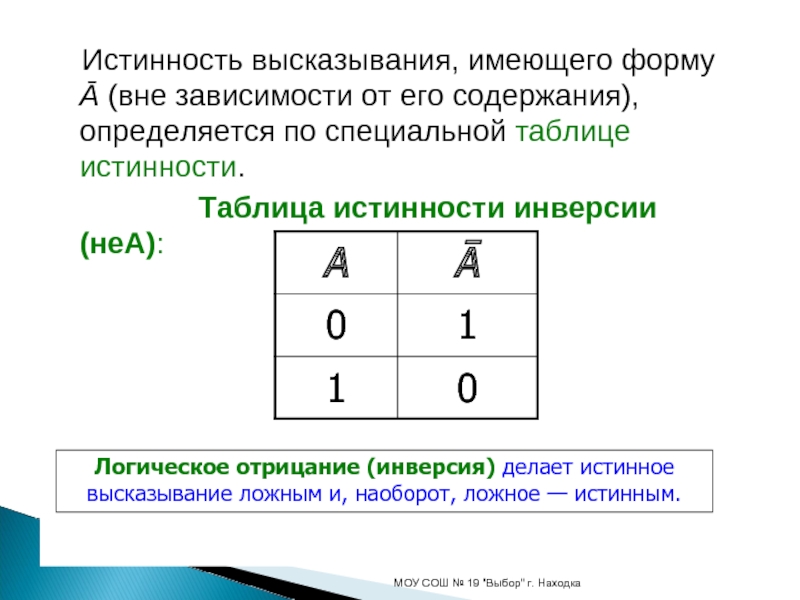
Слайд 4 Истинность высказывания, имеющего форму Ā (вне зависимости от

его содержания), определяется по специальной таблице истинности.

Таблица истинности инверсии (неА):

МОУ СОШ № 19 "Выбор" г. Находка

Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное — истинным.

Истинность высказывания, имеющего форму Ā (вне зависимости от его содержания), определяется по специальной таблице истинности.

Слайд 5Графическая иллюстрация инверсии с помощью диаграмм Эйлера — Венна:

А —

множество отличников;
Ā — множество неотличников.
МОУ СОШ № 19 "Выбор" г.

Находка

Графическая иллюстрация инверсии с помощью диаграмм Эйлера — Венна:А — множество отличников;Ā — множество неотличников.МОУ СОШ №

Слайд 6- образуется соединением двух высказываний в одно с помощью союза

«и».

Обозначение конъюнкции:
A И B;
A ۸ B;
A & B;
A ⋅ B;
A

AND B.

МОУ СОШ № 19 "Выбор" г. Находка

Логическое умножение (конъюнкция)

А = «10 делится на 2»
В = «10 делится на 5» ,
A ۸ B = «10 делится на 2 и на 5».

- образуется соединением двух высказываний в одно с помощью союза «и».Обозначение конъюнкции:A И B;A ۸ B;A &

Слайд 7 Таблица истинности конъюнкции:
МОУ СОШ № 19 "Выбор" г.

Находка
Конъюнкция двух высказываний истинна тогда и только тогда, когда оба

высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.

Таблица истинности конъюнкции:МОУ СОШ № 19

Слайд 8Графическая иллюстрация конъюнкции с помощью диаграмм Эйлера — Венна:

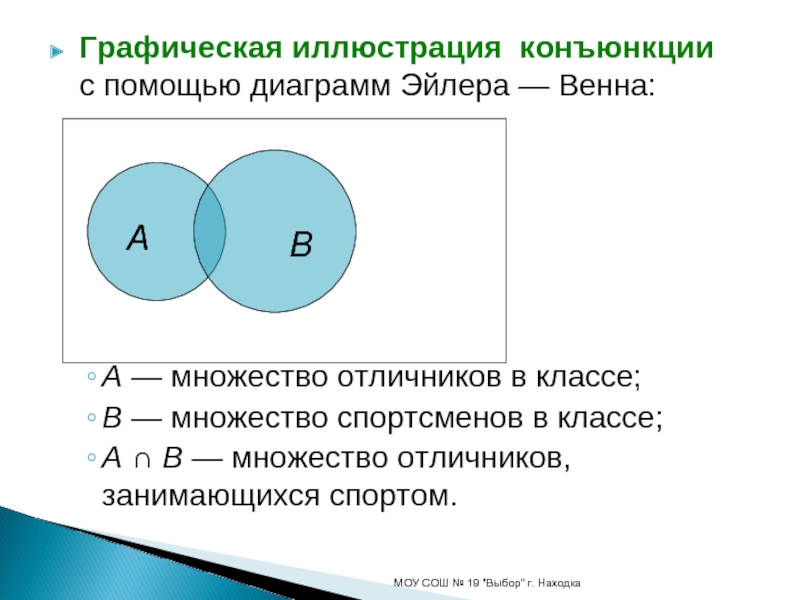
A —

множество отличников в классе;
B — множество спортсменов в классе;
A ∩

B — множество отличников, занимающихся спортом.

МОУ СОШ № 19 "Выбор" г. Находка

Графическая иллюстрация конъюнкции с помощью диаграмм Эйлера — Венна:A — множество отличников в классе;B — множество спортсменов

Слайд 9образуется соединением двух высказываний в одно с помощью союза «или».

Союз

«или» может использоваться:
в неисключающем (объединительном) смысле — операция называется нестрогой

дизъюнкцией;
в исключающем (разделительном) смысле — операция называется строгой дизъюнкцией.

МОУ СОШ № 19 "Выбор" г. Находка

Логическое сложение (дизъюнкция)

образуется соединением двух высказываний в одно с помощью союза «или». Союз «или» может использоваться:в неисключающем (объединительном) смысле —

Слайд 10Примеры строгих и нестрогих дизъюнкций:
МОУ СОШ № 19 "Выбор" г.

Находка

Слайд 11 Под дизъюнкцией будем понимать нестрогую дизъюнкцию, если не

оговорено иное.
Обозначение дизъюнкции:
A ИЛИ B;
A OR B;
A ⏐ B;
A ۷

B;
A + B.

МОУ СОШ № 19 "Выбор" г. Находка

Под дизъюнкцией будем понимать нестрогую дизъюнкцию, если не оговорено иное.Обозначение дизъюнкции:A ИЛИ B;A OR B;A

Слайд 12 Таблица истинности дизъюнкции:
МОУ СОШ № 19 "Выбор" г.

Находка
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба

высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.

Таблица истинности дизъюнкции:МОУ СОШ № 19

Слайд 13Графическая иллюстрация дизъюнкции с помощью диаграмм Эйлера — Венна:

A —

множество отличников в классе;
B — множество спортсменов в классе;
A ∪

B — множество учеников класса, которые являются отличниками или спортсменами.

МОУ СОШ № 19 "Выбор" г. Находка

Графическая иллюстрация дизъюнкции с помощью диаграмм Эйлера — Венна:A — множество отличников в классе;B — множество спортсменов

Слайд 14образуется соединением двух высказываний в одно с помощью оборота речи

«если..., то...».

Обозначение импликации:
A → B;
A ⇒ B.
МОУ СОШ № 19

"Выбор" г. Находка

Логическое следование (импликация)

E = Если клятва дана, то она должна выполняться.
P = Если число делится на 9, то оно делится на 3.

образуется соединением двух высказываний в одно с помощью оборота речи «если..., то...».Обозначение импликации:A → B;A ⇒ B.МОУ

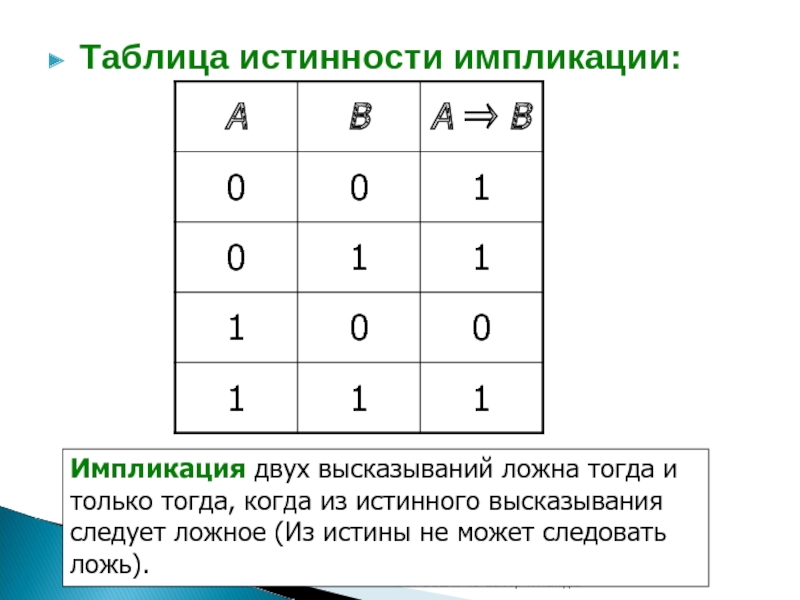
Слайд 15Таблица истинности импликации:
МОУ СОШ № 19 "Выбор" г. Находка
Импликация двух

высказываний ложна тогда и только тогда, когда из истинного высказывания

следует ложное (Из истины не может следовать ложь).

Таблица истинности импликации:МОУ СОШ № 19

Слайд 16Графическая иллюстрация импликации с помощью диаграмм Эйлера — Венна:

(A=0)∩(B=0)
(A=0)∩(B=1)
(A=1)∩(B=1)
МОУ СОШ

№ 19 "Выбор" г. Находка

B
А

Графическая иллюстрация импликации с помощью диаграмм Эйлера — Венна:(A=0)∩(B=0)(A=0)∩(B=1)(A=1)∩(B=1)МОУ СОШ № 19

Слайд 17 образуется соединением двух высказываний в одно при помощи

оборота речи «…тогда и только тогда, когда...».

Обозначение эквивалентности:
A ≡ B;
A

⇔ B;
A ~ B.

МОУ СОШ № 19 "Выбор" г. Находка

Логическое равенство (эквивалентность)

Угол называется прямым тогда и только тогда, когда он равен 90°.
Голова думает тогда и только тогда, когда язык отдыхает.

образуется соединением двух высказываний в одно при помощи оборота речи «…тогда и только тогда, когда...».Обозначение

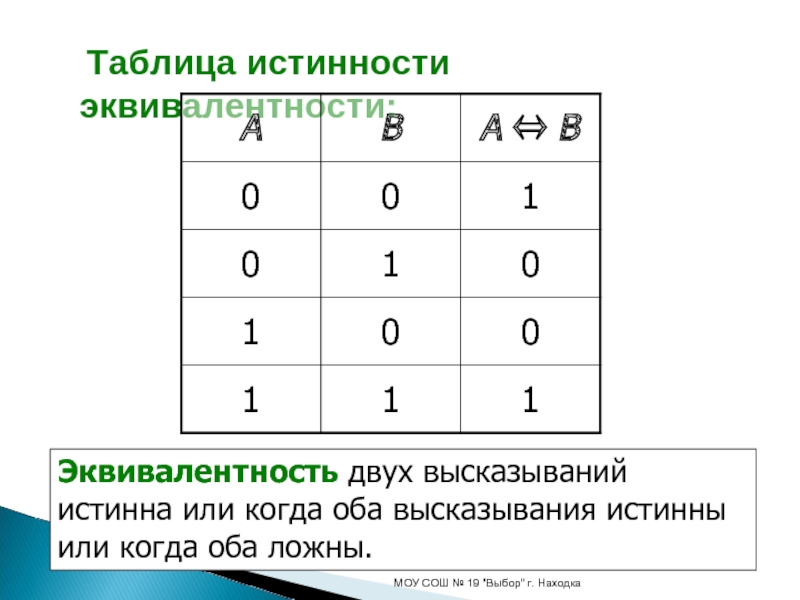
Слайд 18 Таблица истинности эквивалентности:
МОУ СОШ № 19 "Выбор" г.

Находка
Эквивалентность двух высказываний истинна или когда оба высказывания истинны или

когда оба ложны.

Таблица истинности эквивалентности:МОУ СОШ № 19

Слайд 19Графическая иллюстрация эквивалентности с помощью диаграмм Эйлера — Венна:

(A=0)∩(B=0)
(A=1)∩(B=1)
МОУ СОШ

№ 19 "Выбор" г. Находка

B
А

Графическая иллюстрация эквивалентности с помощью диаграмм Эйлера — Венна:(A=0)∩(B=0)(A=1)∩(B=1)МОУ СОШ № 19

Слайд 20Лыскова В.Ю., Ракитина Е.А. Логика в информатике.
Семакин И.Г., Вараксин Г.С.

Информатика. Структурированный конспект базового курса.
Под ред. Семакина И.Г. Информатика. Задачник-практикум

в 2 т. Том 1.
Шауцукова Л.З. Информатика: Учебное пособие для 10-11 классов общеобразовательных учреждений.
Угринович Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов.

МОУ СОШ № 19 "Выбор" г. Находка

Литература

Лыскова В.Ю., Ракитина Е.А. Логика в информатике.Семакин И.Г., Вараксин Г.С. Информатика. Структурированный конспект базового курса.Под ред. Семакина

Скачать презентацию

Теги

Разделы презентаций

Логические операции

Содержание

Слайды и текст этой презентации

Слайд 1Логическое отрицание (инверсия)Логическое умножение (конъюнкция)Логическое сложение (дизъюнкция)Логическое следование (импликация)Логическое равенство

(эквивалентность)МОУ СОШ № 19 "Выбор" г. НаходкаЛогические операции

Слайд 2— способ построения сложного высказывания из данных высказываний, при котором

значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.Истинное

Слайд 3- образуется из высказывания с помощью добавления частицы «не» к

сказуемому или использования оборота речи «неверно, что…».Обозначение инверсии:НЕ А;¬ A;Ā;NOT

Слайд 4 Истинность высказывания, имеющего форму Ā (вне зависимости от

его содержания), определяется по специальной таблице истинности.

Слайд 5Графическая иллюстрация инверсии с помощью диаграмм Эйлера — Венна:А —

множество отличников;Ā — множество неотличников.МОУ СОШ № 19 "Выбор" г.

Слайд 6- образуется соединением двух высказываний в одно с помощью союза

«и».Обозначение конъюнкции:A И B;A ۸ B;A & B;A ⋅ B;A

Слайд 7 Таблица истинности конъюнкции:МОУ СОШ № 19 "Выбор" г.

НаходкаКонъюнкция двух высказываний истинна тогда и только тогда, когда оба

Слайд 8Графическая иллюстрация конъюнкции с помощью диаграмм Эйлера — Венна:A —

множество отличников в классе;B — множество спортсменов в классе;A ∩

Слайд 9образуется соединением двух высказываний в одно с помощью союза «или». Союз

«или» может использоваться:в неисключающем (объединительном) смысле — операция называется нестрогой

Слайд 10Примеры строгих и нестрогих дизъюнкций:МОУ СОШ № 19 "Выбор" г.

Находка

Слайд 11 Под дизъюнкцией будем понимать нестрогую дизъюнкцию, если не

оговорено иное.Обозначение дизъюнкции:A ИЛИ B;A OR B;A ⏐ B;A ۷

Слайд 12 Таблица истинности дизъюнкции:МОУ СОШ № 19 "Выбор" г.

НаходкаДизъюнкция двух высказываний ложна тогда и только тогда, когда оба

Слайд 13Графическая иллюстрация дизъюнкции с помощью диаграмм Эйлера — Венна:A —

множество отличников в классе;B — множество спортсменов в классе;A ∪

Слайд 14образуется соединением двух высказываний в одно с помощью оборота речи

«если..., то...».Обозначение импликации:A → B;A ⇒ B.МОУ СОШ № 19

Слайд 15Таблица истинности импликации:МОУ СОШ № 19 "Выбор" г. НаходкаИмпликация двух

высказываний ложна тогда и только тогда, когда из истинного высказывания

Слайд 16Графическая иллюстрация импликации с помощью диаграмм Эйлера — Венна:(A=0)∩(B=0)(A=0)∩(B=1)(A=1)∩(B=1)МОУ СОШ

№ 19 "Выбор" г. НаходкаBА

Слайд 17 образуется соединением двух высказываний в одно при помощи

оборота речи «…тогда и только тогда, когда...».Обозначение эквивалентности:A ≡ B;A

Слайд 18 Таблица истинности эквивалентности:МОУ СОШ № 19 "Выбор" г.

НаходкаЭквивалентность двух высказываний истинна или когда оба высказывания истинны или

Слайд 19Графическая иллюстрация эквивалентности с помощью диаграмм Эйлера — Венна:(A=0)∩(B=0)(A=1)∩(B=1)МОУ СОШ

№ 19 "Выбор" г. НаходкаBА

Слайд 20Лыскова В.Ю., Ракитина Е.А. Логика в информатике.Семакин И.Г., Вараксин Г.С.

Информатика. Структурированный конспект базового курса.Под ред. Семакина И.Г. Информатика. Задачник-практикум

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

(эквивалентность)

МОУ СОШ № 19 "Выбор" г. Находка
Логические операции

значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

Истинное

сказуемому или использования оборота речи «неверно, что…».

Обозначение инверсии:
НЕ А;
¬ A;
Ā;
NOT

Слайд 5Графическая иллюстрация инверсии с помощью диаграмм Эйлера — Венна:

А —

множество отличников;
Ā — множество неотличников.
МОУ СОШ № 19 "Выбор" г.

«и».

Обозначение конъюнкции:
A И B;
A ۸ B;
A & B;
A ⋅ B;
A

Слайд 7 Таблица истинности конъюнкции:
МОУ СОШ № 19 "Выбор" г.

Находка
Конъюнкция двух высказываний истинна тогда и только тогда, когда оба

Слайд 8Графическая иллюстрация конъюнкции с помощью диаграмм Эйлера — Венна:

A —

множество отличников в классе;
B — множество спортсменов в классе;
A ∩

Слайд 9образуется соединением двух высказываний в одно с помощью союза «или».

Союз

«или» может использоваться:
в неисключающем (объединительном) смысле — операция называется нестрогой

Слайд 10Примеры строгих и нестрогих дизъюнкций:
МОУ СОШ № 19 "Выбор" г.

оговорено иное.
Обозначение дизъюнкции:
A ИЛИ B;
A OR B;
A ⏐ B;
A ۷

Слайд 12 Таблица истинности дизъюнкции:
МОУ СОШ № 19 "Выбор" г.

Находка
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба

Слайд 13Графическая иллюстрация дизъюнкции с помощью диаграмм Эйлера — Венна:

A —

множество отличников в классе;
B — множество спортсменов в классе;
A ∪

«если..., то...».

Обозначение импликации:
A → B;
A ⇒ B.
МОУ СОШ № 19

Слайд 15Таблица истинности импликации:
МОУ СОШ № 19 "Выбор" г. Находка
Импликация двух

Слайд 16Графическая иллюстрация импликации с помощью диаграмм Эйлера — Венна:

(A=0)∩(B=0)
(A=0)∩(B=1)
(A=1)∩(B=1)
МОУ СОШ

№ 19 "Выбор" г. Находка

B
А

оборота речи «…тогда и только тогда, когда...».

Обозначение эквивалентности:
A ≡ B;
A

Слайд 18 Таблица истинности эквивалентности:
МОУ СОШ № 19 "Выбор" г.

Находка
Эквивалентность двух высказываний истинна или когда оба высказывания истинны или

Слайд 19Графическая иллюстрация эквивалентности с помощью диаграмм Эйлера — Венна:

(A=0)∩(B=0)
(A=1)∩(B=1)
МОУ СОШ

№ 19 "Выбор" г. Находка

B
А

Слайд 20Лыскова В.Ю., Ракитина Е.А. Логика в информатике.
Семакин И.Г., Вараксин Г.С.

Информатика. Структурированный конспект базового курса.
Под ред. Семакина И.Г. Информатика. Задачник-практикум