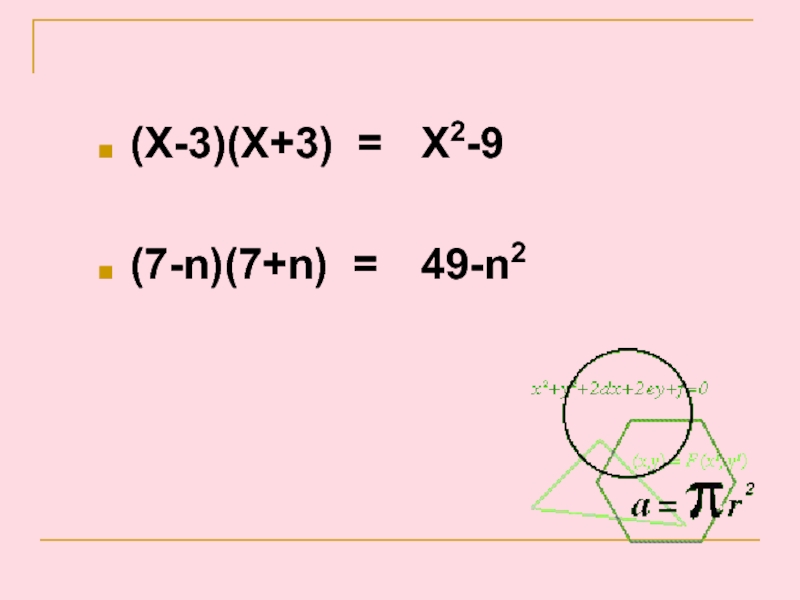Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формулы сокращенного умножения 7 класс
Содержание
- 1. Формулы сокращенного умножения 7 класс
- 2. Цель урока Обобщить и систематизировать
- 3. Математика – царица наук Чтоб врачом, морякомИли
- 4. Организационный момент Французский писатель 19
- 5. Так вот, давайте сегодня на уроке будем
- 6. Исторические сведения. Формулы сокращенного умножения
- 7. Начнем урок с графического диктанта. Вам нужно
- 8. Одночленом называется произведение буквенных и числовых
- 9. А теперь обменяйтесь тетрадями и проверьте правильность
- 10. Кто мне скажет на что похожа
- 11. Повторение формул
- 12. (a+5)2= (3x+y)2=(c+z)2= Как можно записать эти же выражения по-другому (более компактно)?= = = a2+10a+259x2+6xy+y2c2+2cz+z2(a+5)(a+5)(3x+y)(3x+y)(c+z)(c+z)
- 13. Формула квадрата разности(a-b)2=a2-2ab+b2
- 14. (с-6)2= (k-t)2=(4-a)2= Как можно записать эти же выражения по-другому (более компактно)?C2-12c+36K2-2kt+t216-8a+a2(c-6)(c-6)(k-t)(k-t)(4-a)(4-a)
- 15. Разность квадратов двух чиселa2-b2 =(a+b)(a-b)
- 16. (X-3)(X+3) =(7-n)(7+n) =X2-949-n2
- 17. Разность и сумма кубов двух чисел
- 18. Игра «Смотри, не ошибись!» В руках у
- 19. а2 - 4 = (а - 2)
- 20. Тренировочные упражнения
- 21. Проверь себя
- 22. Проверь себя
- 23. Коллективная работа Решение более сложных заданий на
- 24. а) Представить в виде многочлена: (х+1)(х2-х+1)-(х2-1)х =б)
- 25. ФизкультминуткаРаз- подняться, потянутьсяДва- нагнуться, разогнутьсяТри- в ладони
- 26. Работа учащихся в парах Уровень А1.
- 27. Уровень В1) Представьте в виде произведения:
- 28. Уровень С1) Представьте в виде произведения: 5
- 29. Проверочная таблица
- 30. Работу учащиеся оценивают самостоятельно, используя таблицу
- 31. Выполнение тестовых заданий Тест № 1Что будет
- 32. Карточка самооценки учащегося
- 33. Итог урока Оценка труда учащихся:а) самооценка –
- 34. Подведение итогов урока Когда греков завоевали
- 35. СПАСИБО ЗА ВНИМАНИЕ!
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Математика – царица наук
Чтоб врачом, моряком
Или летчиком стать,
Надо
многое знать,
Надо много уметь.
И при этом, и при этом,
Вы заметьте-ка,
Очень
важная наука А р и ф м е т и к а !
Слайд 4Организационный момент
Французский писатель 19 столетия Анатоль Франс
однажды заметил: ”Учиться можно только весело, чтобы переварить знания, надо
поглощать их с аппетитом.”Слайд 5 Так вот, давайте сегодня на уроке будем следовать этому совету
писателя, будем активны, внимательны, будем поглощать знания с большим желанием,
ведь они пригодятся вам в вашей дальнейшей жизни. Тема нашего урока: «Формулы сокращенного умножения». Сегодня - последний урок по данной теме перед контрольной работой. Перед вами стоит задача - показать, как вы знаете формулы сокращенного умножения и умеете их применять.Слайд 6Исторические сведения.
Формулы сокращенного умножения были известны еще 4000
лет назад. Ученые Древней Греции представляли величины не числами или
буквами, а отрезками прямых.Вместо «произведение ав» говорилось «прямоугольник, содержащийся между а и в»,вместо а2 «квадрат на отрезке а».
В книге Евклида «Начала» правило квадрата суммы выражается так: «если прямая линия как-либо рассечена точкой С, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключенным между отрезками.
Слайд 7Начнем урок
с графического диктанта.
Вам нужно ответить на предложенные
вопросы “да” или “нет”.
При ответе “да” рисуете в тетради
отрезок, а при ответе “нет” - уголок. Каждый последующий ответ пририсовывается к предыдущему.
Слайд 8 Одночленом называется произведение буквенных и числовых множителей.
Выражение 2х2у4х
– одночлен в стандартном виде.
Алгебраическая сумма одночленов называется многочленом.
Квадрат двучлена
(а – 2в) равен а2 – 2ав + 4в2.а2 + в2 – одна из формул сокращенного умножения.
Выражение х2 – у2 представляет собой разность квадратов.
Выражение (х + у)3 – формула суммы кубов.
Выражение (х – у)2 = х2 – у2.
Выражение х3 – 8у3 = (х – 2)(х2 + 2х + 4).
Выражение х2 + 2х + 4 называется неполным квадратом суммы х и 2.
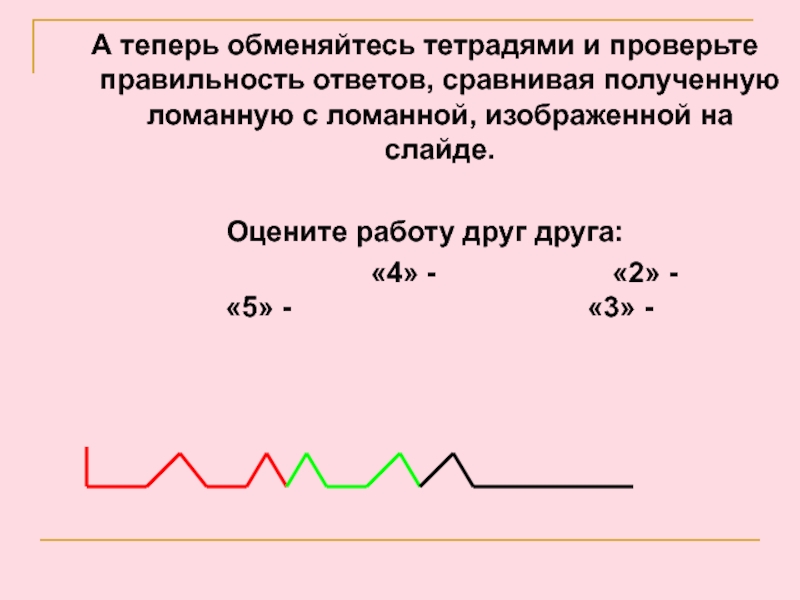
Слайд 9А теперь обменяйтесь тетрадями и проверьте правильность ответов, сравнивая полученную
ломанную с ломанной, изображенной на слайде.
Оцените работу друг друга:
«4» - «2» - «5» - «3» -
Слайд 10 Кто мне скажет на что похожа наша ломаная?
(на
кардиограмму).
Вы составили ее верно, значит сердце в норме,
настроение
хорошее, ивы готовы к дальнейшей работе.
Слайд 12(a+5)2=
(3x+y)2=
(c+z)2=
Как можно записать эти же выражения
по-другому (более
компактно)?
=
=
=
a2+10a+25
9x2+6xy+y2
c2+2cz+z2
(a+5)(a+5)
(3x+y)(3x+y)
(c+z)(c+z)
Слайд 14(с-6)2=
(k-t)2=
(4-a)2=
Как можно записать эти же выражения
по-другому (более
компактно)?
C2-12c+36
K2-2kt+t2
16-8a+a2
(c-6)(c-6)
(k-t)(k-t)
(4-a)(4-a)
Слайд 17Разность и сумма кубов
двух чисел
а 3 –
b 3 =
а 3 + b 3 =
(a –
b )(a 2 + a b + b 2)(a + b )(a 2– a b + b 2)
Слайд 18Игра «Смотри, не ошибись!»
В руках у учеников сигнальные карточки.
Верно-
X - «крестики»
Неверно О - «нолики».
Слайд 19
а2 - 4 = (а - 2) (а + 2)
а3 + 1 = (a + 1)( а2 + а
+ 1)(1 + b)2 = 2 + 2b + b2
х3 - 8 = (х2 – 2)(х - 2х + 4)
(а + 3)2 = a2 + 6a + 9
(х2 - 1) = (1 + x)(x - 1)
472 – 372=(47 - 37)(47 + 37)
Х
О
О
О
Х
Х
Х
Слайд 23Коллективная работа
Решение более сложных заданий на применение формул сокращенного
умножения (комментирование с места или у доски).
а) Представить в виде
многочлена: (х+1)(х2-х+1)-(х2-1)х
б) Упростить выражение и найти его значение при х = – 0,2:
(4х + 1)2 – (4х – 1)2
в) Решите уравнение:
(х – 1)(х + 1) – х(х – 3 ) = 2 (х - 1)
г) Вычислить
1012
д)Вычислить
48*52
Слайд 24а) Представить в виде многочлена:
(х+1)(х2-х+1)-(х2-1)х =
б) Упростить выражение и
найти его значение при х = – 0,2:
(4х + 1)2
– (4х – 1)2 =в) Решите уравнение:
(х – 1)(х + 1) – х(х – 3 ) = 2(х-1)
г) Вычислить:
1012
д) Вычислить:
48*52
Слайд 25Физкультминутка
Раз- подняться, потянуться
Два- нагнуться, разогнуться
Три- в ладони три хлопка
Головою три
кивка
На четыре руки шире
Пять- руками помахать
Шесть- на место тихо сесть
Слайд 26Работа учащихся в парах
Уровень А
1. Представьте в виде
произведения:
а) х3 – у3
б) а3 + 64
2. Преобразуйте в двучлен:
а) (p – q)(p2 + pq + q2);
б) (а – 3)(а2 + 3а + 9)
в) (2m + n)(4m2 – 2mn + n2)
Слайд 27Уровень В
1) Представьте в виде произведения:
а) m6 –
216; б)125 – b12;
2) В равенстве
… + … =
(… + n2) (9m2 – …+…) заполните пропуски одночленами так, чтобы получилось верное равенство;3) Представьте в виде многочлена
a3- (a-4)(a2+4a+16).
Слайд 28Уровень С
1) Представьте в виде произведения:
5 (m – n)
+ (m3 – n3)
2) Упростить:
2х2-у)2-х4
3) Упростить:
( х+1)(х2-х+1)-(х2-1)Х
Слайд 30
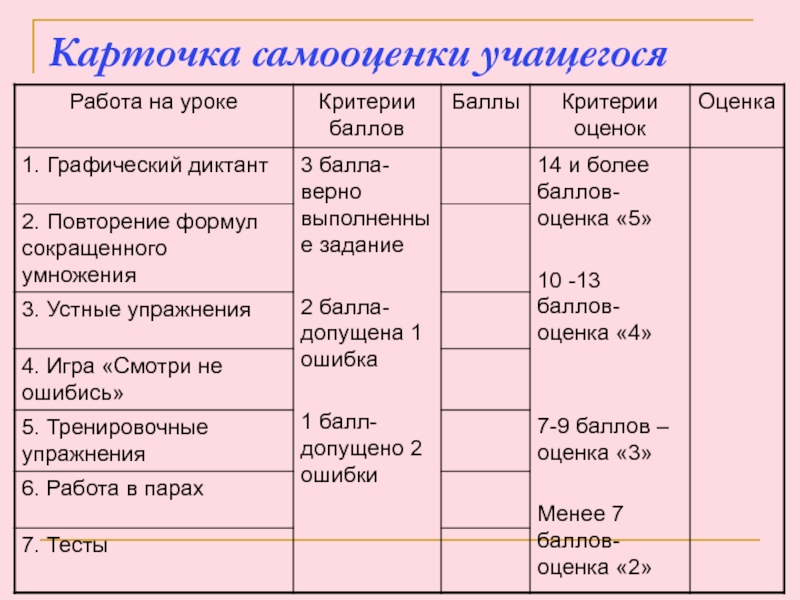
Работу учащиеся оценивают самостоятельно, используя таблицу ответов и следующие критерии:
1.
Решил сам – “3” балла.
2. Решил сам, но консультировался у
товарища – “2” балла.3. Решал с помощью товарища или учителя – “1” балл.
Слайд 31Выполнение тестовых заданий
Тест № 1
Что будет решением для данного
выражения:
1. (х + 2у)2 =
а) х2 + 4ху + 4у2
в) х2 + 4у2 б) х2 + 4ху + 2у2 г) х2 + 2ху + 2х2
2. (3а – 2)2=
а) 9а2 – 6а + 4 в) 9а2 – 12а + 4
б) 3а2 – 12а + 4 г) 9а2 – 4
3. (3х – 5у) (3х + у ) =
а) 9х2 – 25у2 в) 9х2 + 25у2
б) 9х2 + 25у4 г) 9х2 – 25у4
4. (а – 2) (а2 + 2а + 4) =
а) а3 – 8 в) а3 + 8
б) а3 – 2а2 + 8 г) а3 – 16
5. Даны два равенства:
1) (2а – 3в2)2 = 4а2 – 6ав2 + 9в4
2) (х + 3у)2 = х2 + 9у2 + 6ху
Какое из них верно (да), а какое неверно (нет)?
а) да, да б) да, нет в) нет, да г) нет, нет
Тест № 2
Что будет решением для данного выражения:
1. (3а + в)2=
а) 9а2 + в2 в) 9а2 + 3ав + в2
б) 9а2 + 6ав + в2 г) 3а2 + 6ав + в2
2. (2а – 3)2=
а) 4а2 – 6а + 9 в) 2а2 – 12а + 9
б) 4а2 – 12а + 9 г) 4а2 – 9
3. (2х – 3у)(2х + 3у2) =
а) 4х2 – 9у4 в) 4х2 + 9у2
б) 4х2 – 9у2 г) 4х2 + 9у4
4. (х + 1)(х2 – х + 1) =
а) х3 + х2 – 1 в) х3 – х2 – 1
б) х3 – 1 г) х3 + 1
5. Даны два равенства:
1) (3х2 + 2у)2 = 4у2 + 12х2у + 9х4
2) (3а – в)2 = 9а2 + в2 – 6ав
Какое из них верно (да), а какое неверно (нет)?
а) да, да б) да, нет в) нет, да г) нет, нет
Слайд 33Итог урока
Оценка труда учащихся:
а) самооценка – усвоена ли тема
полностью, что вызвало затруднения и требует повторения, в каких знаниях
уверен;б) учениками – кто, по вашему мнению, работал лучше всех, кому и над чем следует еще поработать
в) учителем – оценивается работа класса (активность, уровень знаний, умений, навыков, самоорганизации, прилежание)
Слайд 34Подведение итогов урока
Когда греков завоевали римляне, развитие математики
надолго остановилось. На целую тысячу лет! Возродили математику арабы. Когда-то
очень давно жил выдающийся поэт, математик Омар Хайям:Мне мудрость не чужда была земная,
Разгадки тайн ища, не ведал сна я.
За семьдесят перевалило мне,
Что ж я узнал!...
Что ничего не знаю.