Тригонометрические функции числового аргумента. График и свойства функции у=sin x

функции числового аргумента. График

и свойства функции у= sin x».

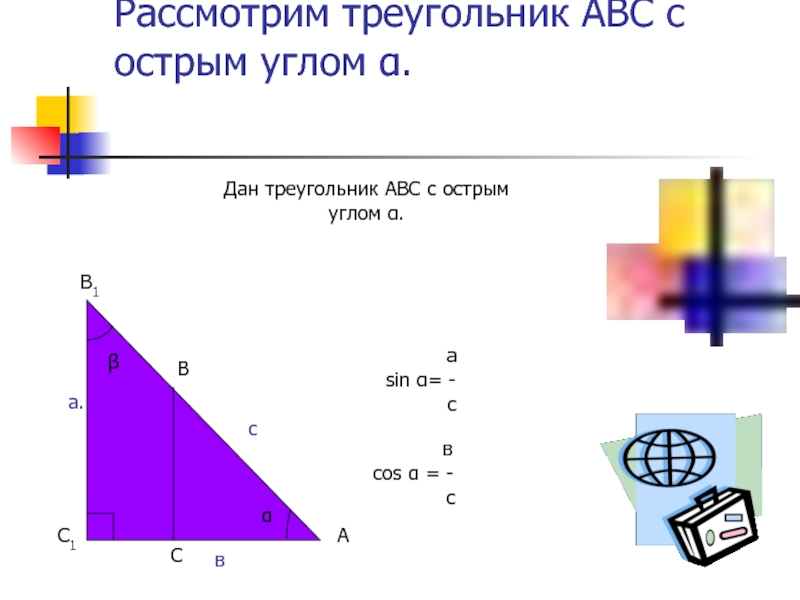
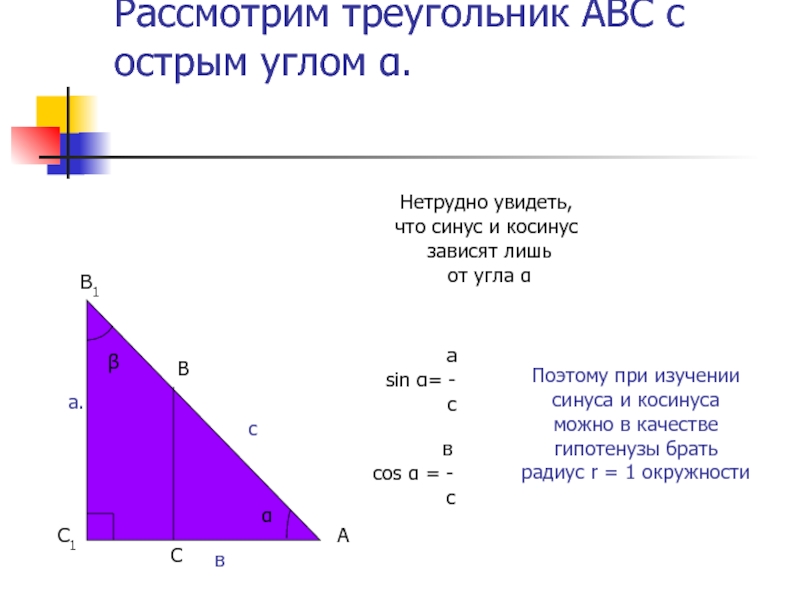
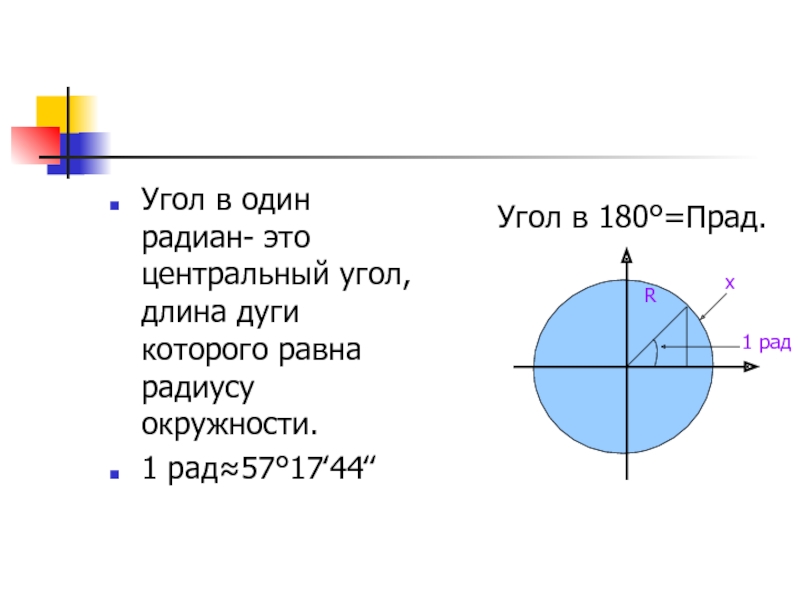
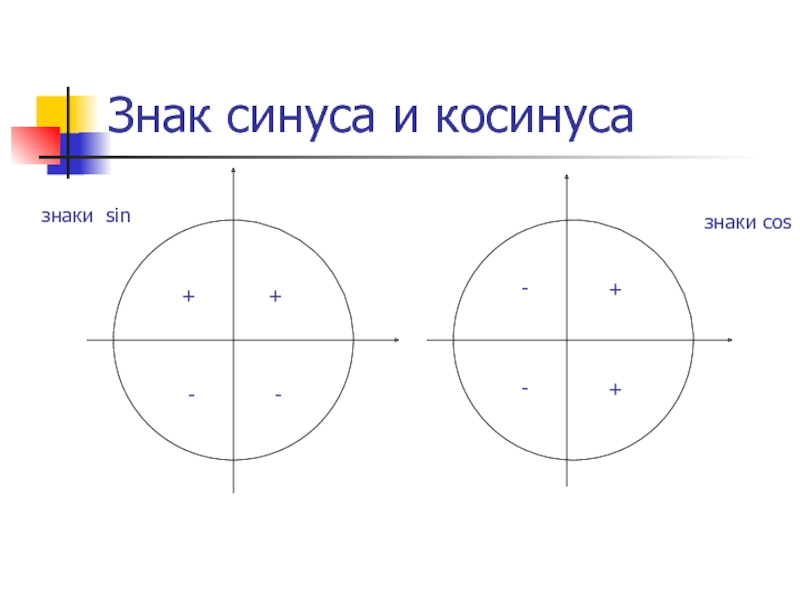
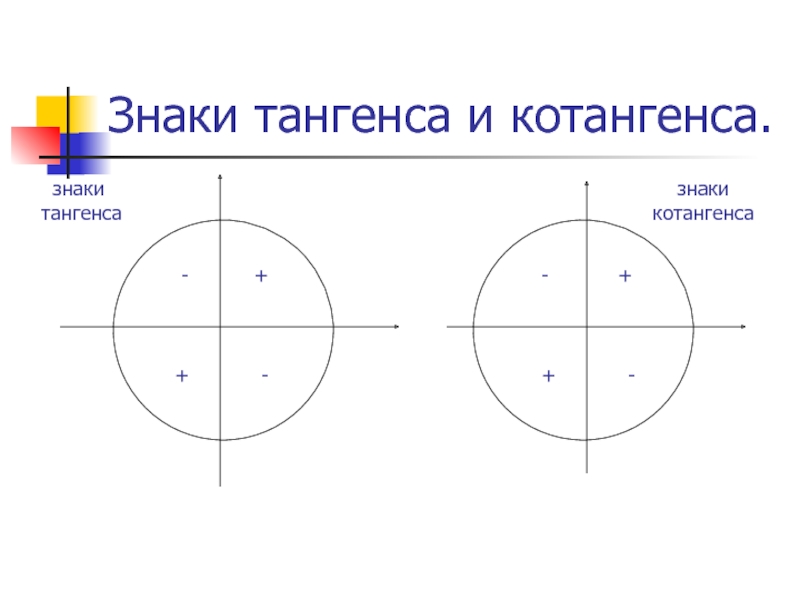
Цели урока:1) повторить и систематизировать знания о мерах углов, понятии синуса, косинуса, тангенса и котангенса;
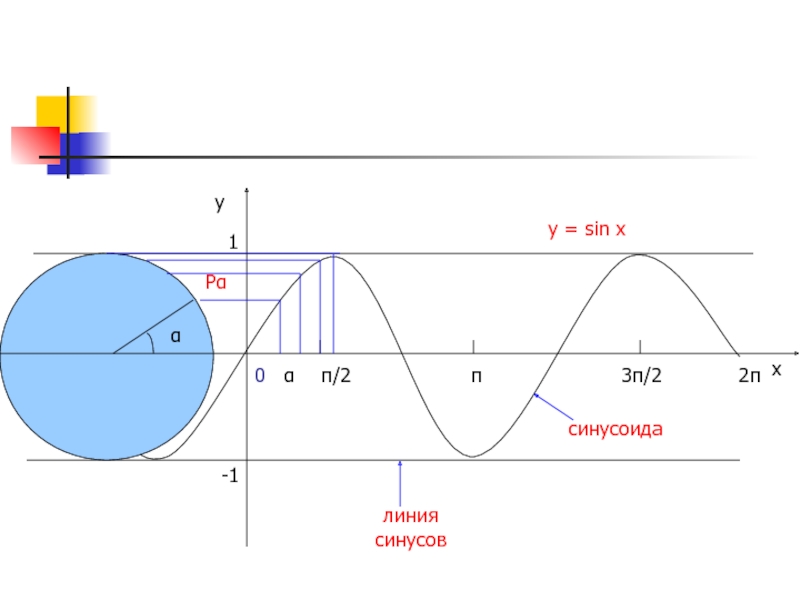
2) ввести понятие функции синуса;
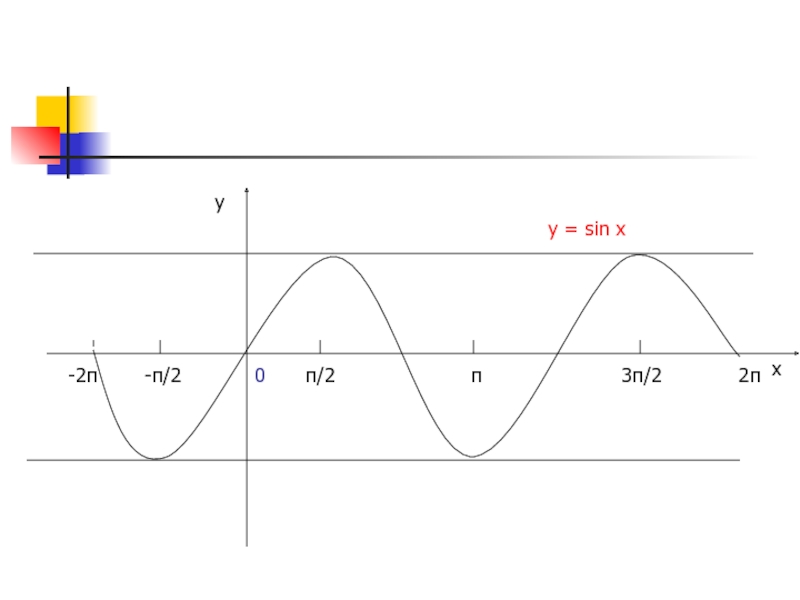
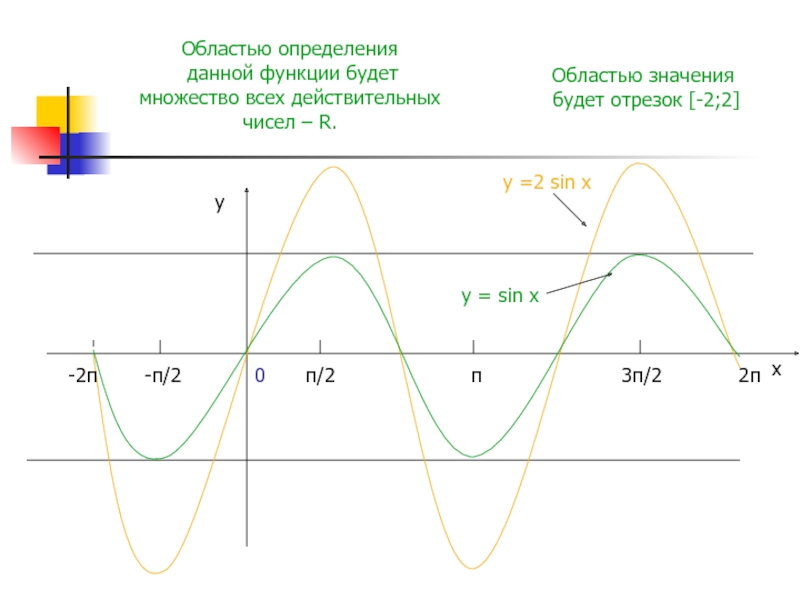
3) научиться строить график функции у = sin x;
4) Изучить свойства функции у = sin x;
5) способствовать развитию практических умений и навыков.

Тема урока:

28.10.2010 г.

а
sin α= -
с

в
cos α = -
с

Дан треугольник АВС с острым углом α.

а.

с

в

В

С

α
____
sin α
cos α
=
ctg α
tg² α + 1 =
____
cos² α
1
ctg² α

+ 1 =

sin² α

____

1

Основные тригонометрические тождества

(теорема Пифагора, перефразированная с помощью понятия о синусе и косинусе )

а
sin α= -
с

в
cos α = -
с

Нетрудно увидеть,
что синус и косинус
зависят лишь
от угла α

а.

с

в

Поэтому при изучении
синуса и косинуса
можно в качестве
гипотенузы брать
радиус r = 1 окружности

В

С

углы,
смысла иметь не будет.

равна радиусу окружности.
1 рад≈57°17‛44‛‛
Угол в 180°=Πрад.

R

1 рад

x

Делается это путем построения следующего отображения множества углов в

числовое множество. Другими словами градусы переводят в числа.

– множество всех действительных чисел. Обозначается: D (sin x)

= R.
Областью значения функции синус является отрезок [- 1; 1], поскольку и ординаты, и абсциссы точек единичной окружности принимают все значения от -1 до 1. Обозначается: Е (sin x) = [- 1; 1].
Еще известными свойствами этой функции является то, что для любого х справедливы следующие равенства:
sin (-x) = - sin x;
sin x = 0, при х = πn, n € Z (Z – множество всех целых чисел);
sin x = 1, при х = π/2 + 2πn, n € Z;
sin x = -1, при х = - π/2 + 2πn, n € Z.
На отрезке [- π/2; π/2] функция синуса является строго монотонно возрастающей;
функция четная;
периодическая, с установленным периодом 2π.
функция непрерывна.

будет
множество всех действительных чисел – R.
Областью значения
будет отрезок [-2;2]

область
определения и
область значения
функции у = 1/2 sin x.
Постройте ее график.
ІІ

вариант
Найдите область
определения и
область значения
функции у = 3 sin x.
Постройте ее график.

= sin x.
2) Найдите область определения и область значения функций:

у = -1/2 sin x,
у = sin 3x,
у =3 + sin x. Постройте их графики.