Векторы на плоскости

Содержание

1. Векторы на плоскости
2. СОДЕРЖАНИЕВекторные величиныВекторПостроение вектораАбсолютная величина. Равные векторы Нулевой
3. Векторные величины
4. АВЕКТОРГеометрически векторы изображаются направленными отрезками.
5. От любой точки можно отложить вектор, равный
6. Абсолютная величина. Равные векторы.
7. Нулевой вектор. Нулевой вектор -
8. Коллинеарные вектораДва ненулевых вектора называются коллинеарными, если
9. Сонаправленные и противоположно направленные вектора Если векторы
10. Если векторы а и в коллинеарны и
11. Скачать презентанцию

СОДЕРЖАНИЕВекторные величиныВекторПостроение вектораАбсолютная величина. Равные векторы Нулевой векторКоллинеарные векторыСонаправленные векторы, противоположно направленные векторыСвойство коллинеарных векторов

Слайды и текст этой презентации

Слайд 1

ВЕКТОРЫ НА

ПЛОСКОСТИ

Слайд 2СОДЕРЖАНИЕ
Векторные величины
Вектор
Построение вектора
Абсолютная величина. Равные векторы
Нулевой вектор
Коллинеарные векторы
Сонаправленные векторы,

противоположно направленные векторы
Свойство коллинеарных векторов

СОДЕРЖАНИЕВекторные величиныВекторПостроение вектораАбсолютная величина. Равные векторы Нулевой векторКоллинеарные векторыСонаправленные векторы, противоположно направленные векторыСвойство коллинеарных

Слайд 3
Векторные величины

Величины, которые характеризуются не только числом, но и еще

и направлением, называются векторными величинами или просто векторами.

Скорость
Ускорение
Сила

Векторные величины Величины, которые характеризуются не только числом, но

Слайд 4А
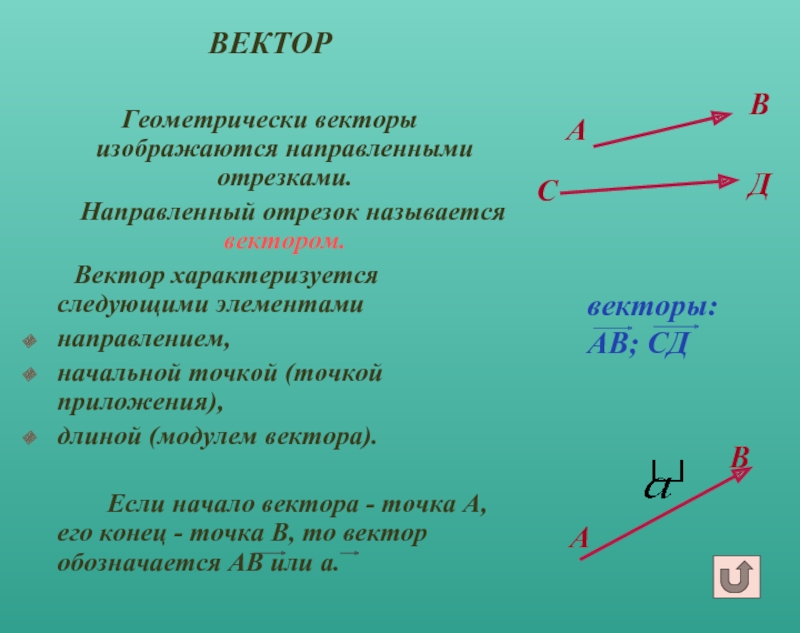
ВЕКТОР

Геометрически векторы изображаются направленными отрезками.

Направленный отрезок называется вектором.
Вектор характеризуется следующими

элементами
направлением,
начальной точкой (точкой приложения),
длиной (модулем вектора).

Если начало вектора - точка А, его конец - точка В, то вектор обозначается АВ или а.

векторы: АВ; СД

АВЕКТОРГеометрически векторы изображаются направленными отрезками. Направленный отрезок называется вектором.

Слайд 5От любой точки можно отложить вектор, равный данному, и притом

только один, используя параллельный перенос.

MN =

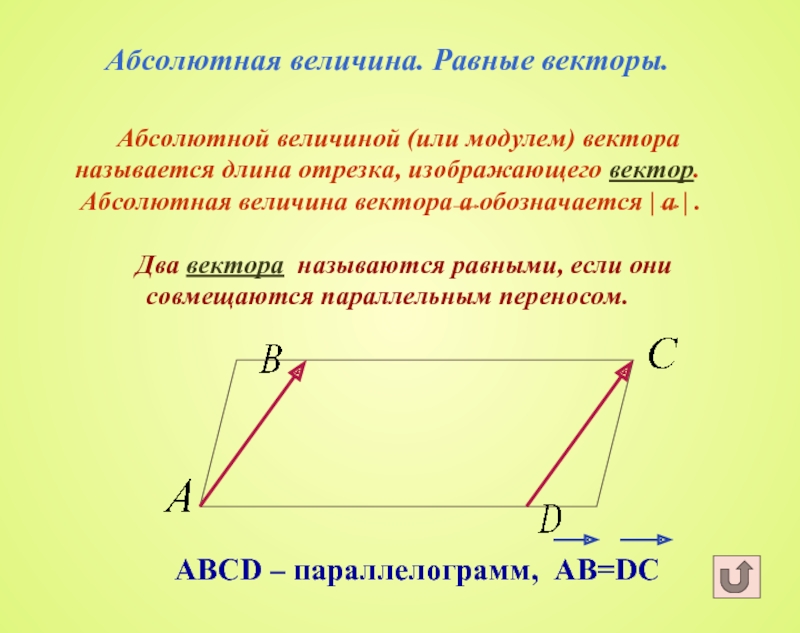
Слайд 6 Абсолютная величина. Равные векторы. Абсолютной величиной (или модулем)

вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора а

обозначается | а | . Два вектора называются равными, если они совмещаются параллельным переносом.

АВСD – параллелограмм, АВ=DС

Абсолютная величина. Равные векторы. Абсолютной величиной (или модулем) вектора называется длина

Слайд 7 Нулевой вектор. Нулевой вектор - точка в пространстве. Начало и конец

нулевого вектора совпадают, и он не имеет направления. Длина нулевого вектора

равна нулю. Обозначается |О|.

Нулевой вектор. Нулевой вектор - точка в пространстве. Начало и конец нулевого вектора совпадают,

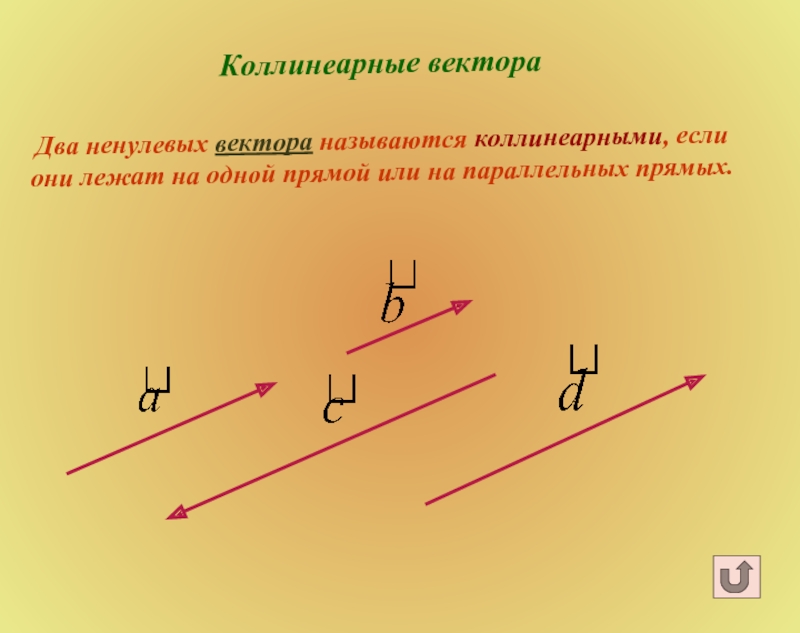
Слайд 8Коллинеарные вектора

Два ненулевых вектора называются коллинеарными, если они лежат на

одной прямой или на параллельных прямых.

Слайд 9Сонаправленные и противоположно направленные вектора

Если векторы а и в

коллинеарны и их лучи сонаправлены, то векторы а и в

называются сонаправленными. Обозначаются а в.

Если векторы а и d коллинеарны, а их лучи не являются сонаправленными, то векторы а и d называются противоположно направленными. Обозначаются а d.
Нулевой вектор условились считать сонаправленным с любым вектором.

Сонаправленные и противоположно направленные вектора Если векторы а и в коллинеарны и их лучи сонаправлены, то векторы

Слайд 10Если векторы а и в коллинеарны и а=0, то существует

число к такое, что в = к а, причем если

к>0, то векторы а и в сонаправленные и а=0, то существует число к такое, что в = к а, причем если к>0, то векторы а и в сонаправленные, если к<0, то противоположно направленные.

Свойство коллинеарных векторов