Математика - абстрактная наука или окружающий нас мир?

миром!»-провозгласил Пифагор, когда установил связь (функциональную зависимость) между длиной струны

музыкального инструмента и издаваемым им звуком. Соответствие чисел окружающему миру по Пифагору:
1-огонь 2-земля 3-вода 4-воздух. Четные числа – женские Нечетные – мужские
5- бракосочетание (3+2)
6- совершенство
220,284- дружба

можно рассмотреть доказательства, в которых квадрат, построенный на гипотенузе данного

прямоугольного треугольника «складывается» из таких же фигур, что и квадраты, построенные на катетах. Можно рассматривать и такие доказательства, в которых применяется перестановка слагаемых фигур и учитывается ряд новых идей.

На рис. 2 изображено два равных квадрата. Длина сторон каждого квадрата равна a + b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a, b, то останутся равные площади, т. е. c2 = a2 + b2. Впрочем,древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «смотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.

т.е. имеет пять осей симметрии, которые
совмещаются при каждом повороте на

72о. Именно это тип симметрии наиболее распространён в живой природе у цветков незабудки, гвоздики, колокольчика, шиповника, лапчатки гусиной, вишни (рис. 5), груши, яблони, малины,
26 «Теорема Пифагора»
рябины и т.д. Поворотная симметрия пятого порядка встречается и в живот-
ном мире, например, у морской звезды (рис. 6) и панциря морского ежа.

Рис. 6

Рис. 5

на гипотенузе прямоугольного треугольника,
равна сумме площадей квадратов, построенных на его

катетах». Действительно,
с2 – площадь квадрата, построенного на гипотенузе, а2 и b2 – площади квадратов, построенных на катетах (рис. 8).

Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Квадрат, построенный
на гипотенузе, содержит четыре треугольника. А на каждом катете построен
квадрат, содержащий два треугольника. Из рисунка 9 видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким

простым путём
К результату мы придём.

Отрубил Иван-царевич дракону голову, а у него две новые выросли. На
математическом языке это означает: провели в D АВС высоту CD и образовалось два новых прямоугольных треугольника ADC и BDC.
Вспомнив этот рисунок, вы вспомните дополнительное построение и начало доказательства теоремы.
Теорема Пифагора – одна из главных теорем геометрии, потому что с её
помощью можно доказать много других теорем и решить множество задач.
Особенностью теоремы Пифагора является то, что она неочевидна. На-
пример, свойства равнобедренного треугольника можно увидеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак
не увидишь, что его стороны находятся в соотношении с 2= а 2+ b2

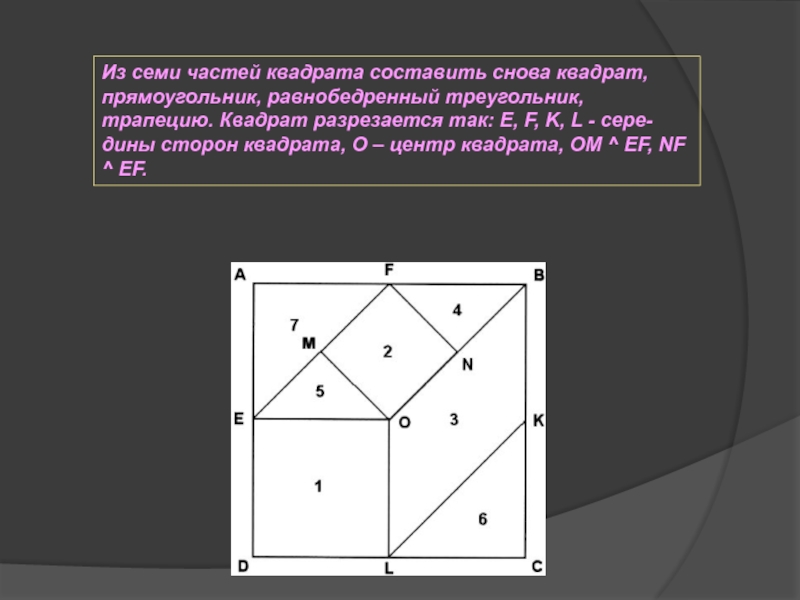
биографии Пифагора.
Сорок лет, возраст акмевершина творческих сил человека - стал

и временем рас-
цвета философии Пифагора.
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства
или тайного монашеского ордена, члены которого обязывались вести так
называемый пифагорейский образ жизни - это был одновременно и религиозный со-
юз, и политический клуб, и научное общество. Он быстро завоевал широкую
известность и стал ведущим центром духовной и общественной жизни.
Не только сила личности и мудрость Пифагора, но и высокая
нравственность проповедуемых им идей и жизненных принципов притягивала к нему
единомышленников, которые и сегодня достойны подражания.
Система морально-этических правил, завещанная ученикам Пифагора,
была собрана в своеобразный моральный кодекс пифагорейцев - «Золотые стихи».
Они переписывались и дополнялись па протяжении всей тысячелетней
истории античности, а затем и в эпоху средневековья и Возрождения. В 18-19 в.в.
«Золотые стихи» были особенно популярны в России. В 1808 году в Санкт-
Петербурге вышла карманного формата книжечка «Пифагоровы законы и
нравственные правила», начинавшаяся словами:

Зороастр был законодателем персов.
Ликург был законодателем спартанцев.
Солон был законодателем афинян.
Нума был законодателем римлян.
Пифагор есть законодатель всего человеческого рода.

одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол

прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

«Имеется водоем со стороной в
1 чжан = 10 чи. В центре его растет
камыш, который выступает над водой
на 1 чи. Если потянуть камыш к бере-
гу, то он как раз коснётся его. Спраши-
вается: какова глубина воды и какова
длина камыша?».

трапецию. Квадрат разрезается так: E, F, K, L - сере-
дины

сторон квадрата, О – центр квадрата, ОМ ^ EF, NF ^ EF.