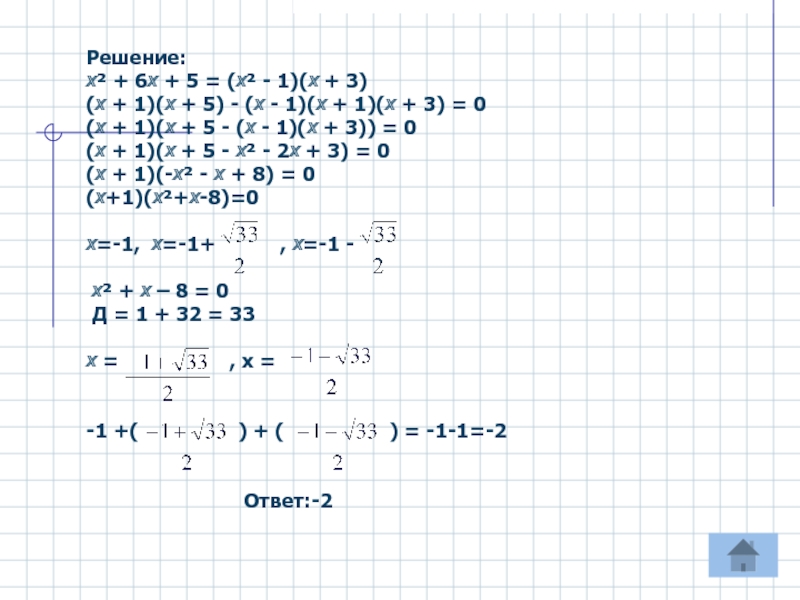Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения уравнений третьей степени
Содержание
- 1. Методы решения уравнений третьей степени
- 2. 1. Простейший методA1. Решить уравнениех³ = 8и выберите правильный ответ:-2-2; 2;0; ;2;- .
- 3. 2. Графический методA2. Найти решение уравнения -
- 4. 3. Способ группировкиА3. Среднее арифметическое всех корней
- 5. Решение:х³ - 3х² - 4х + 12
- 6. Способ группировкиВ1.б) Найдите сумму корней уравнения х²
- 7. Решение:х² + 6х + 5 = (х²
- 8. Способ группировкив) Решение уравнений с модулем. Найдите
- 9. Решение:(-х + 2)х² = 18 - 9х-х³
- 10. 4. Метод подбора.Решить уравнение:х³ - 3х² - 4х + 12 = 0 Решение
- 11. делители 12: ±1;±2;±3;±4;±6;±12 -1 не подходит +1
- 12. 5. Искусственный методА4. Если многочленх³ + 2,5х²
- 13. Решение:х³ + 2,5х² + 5х + 2
- 14. Молодец!
- 15. Подумай ещё!Этот ответ неверен
- 16. Скачать презентанцию
1. Простейший методA1. Решить уравнениех³ = 8и выберите правильный ответ:-2-2; 2;0; ;2;- .
Слайды и текст этой презентации
Слайд 1Методы решения уравнений третьей степени.
Простейший.
Графический.
Способ группировкиСпособ группировки (АСпособ группировки
(А, ВСпособ группировки (А, В, С)
Слайд 32. Графический метод
A2. Найти решение уравнения - x3 = x
+ 2 в заданном промежутке:
1. 1. (0; +);
2. (-1; 0);
3.
[-1; 0);4. (-; -1);
5. (-3; -2].
Слайд 43. Способ группировки
А3. Среднее арифметическое всех корней уравнения
х³ - 3х² - 4х + 12 = 0
равно
1)
-1;4) 2/3;
5) -3.
2) 1/3;
3) 1;
Слайд 5Решение:
х³ - 3х² - 4х + 12 = 0
х² (х
- 3) - 4(х - 3) = 0
(х - 3)(х²
- 4) = 0(х - 3)(х - 2)(х + 2) = 0
х = 3, х = 2, х = -2
(3+2+(-2))/3=1
Ответ:3 (записывают на листах ЕГЭ ответ)
Слайд 7Решение:
х² + 6х + 5 = (х² - 1)(х +
3)
(х + 1)(х + 5) - (х - 1)(х
+ 1)(х + 3) = 0(х + 1)(х + 5 - (х - 1)(х + 3)) = 0
(х + 1)(х + 5 - х² - 2х + 3) = 0
(х + 1)(-х² - х + 8) = 0
(х+1)(х²+х-8)=0
х=-1, х=-1+ , х=-1 -
х² + х – 8 = 0
Д = 1 + 32 = 33
х = , х =
-1 +( ) + ( ) = -1-1=-2
Ответ:-2
Слайд 8Способ группировки
в) Решение уравнений с модулем. Найдите наибольший корень уравнения
|х
- 2|х² = 18 - 9х
! обратить внимание х²:
18 -
9х ≥ 0,х ≤ 2.
Решение
Слайд 9Решение:
(-х + 2)х² = 18 - 9х
-х³ + 2х² -
18х + 9х = 0
х²(-х + 2) - 9(2 -
х) = 0(2 - х)(х² - 9) = 0
х = 2, х = 3, х = -3
удовл.усл. не удовл.усл. удовл.усл.
х≤2 х≤2 х≤2
Ответ: 2
Слайд 11делители 12: ±1;±2;±3;±4;±6;±12
-1 не подходит
+1 не подходит
-2 подходит:
(-8-12+8+12)=0 0=0(верно)
х²-5х+6=0 х1=2, х2=3 Ответ: -2;2;3
х³-3х²4х+12|_х+2_
Решение
x2-5x+6
х³+2х²
-5х²-4х
-5х²-10х
6х+12
6х+12
0
Слайд 125. Искусственный метод
А4. Если многочлен
х³ + 2,5х² + 5х +
2
можно представить в виде
(2х + 1)(ах² + bх + с),
то
сумма а+b+с равна5) 5.
4) 3,5;
2) 2,5;
1) 4,51) 4,5;
3) 3;
Решение
Слайд 13Решение:
х³ + 2,5х² + 5х + 2 = (2х +
1)(ах² + bх + с)
х³+2,5х²+5х+2=2ах³+2bх²+2хс+ах²+bх+с
2а=1, а
= = 0,5 а = 0,52,5=2b + а с = 2
5 = 2с+ b = 1
с = 2
а + b + с = 0,5 + 2 + 1 = 3,5
Ответ: 3,5
Теги
