Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Многогранники"
Содержание
- 1. "Многогранники"
- 2. Цели:Познакомиться с новым типом многогранников - правильными
- 3. « Правильных многогранников вызывающе мало, но этот
- 4. Определение правильного многогранникаМногогранник называется правильным, если все
- 5. С глубокой древности человеку известны пять удивительных
- 6. ТетраэдрТетраэдр (tetra – четыре, hedra – грань).
- 7. Элементы симметрии: Тетраэдр не имеет центра симметрии,
- 8. Гексаэдр(куб)Гексаэдр (куб, hexa – шесть). Гексаэдр –
- 9. Элементы симметрии: Куб имеет центр симметрии -
- 10. ОктаэдрОктаэдр (okto – восемь). Это правильный многогранник,
- 11. Элементы симметрии: Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
- 12. ДодекаэдрСуществует правильный многогранник, у которого все грани
- 13. Элементы симметрии: Додекаэдр имеет центр симметрии -
- 14. ИкосаэдрСуществует правильный многогранник, у которого все грани
- 15. Элементы симметрии: Икосаэдр имеет центр симметрии -
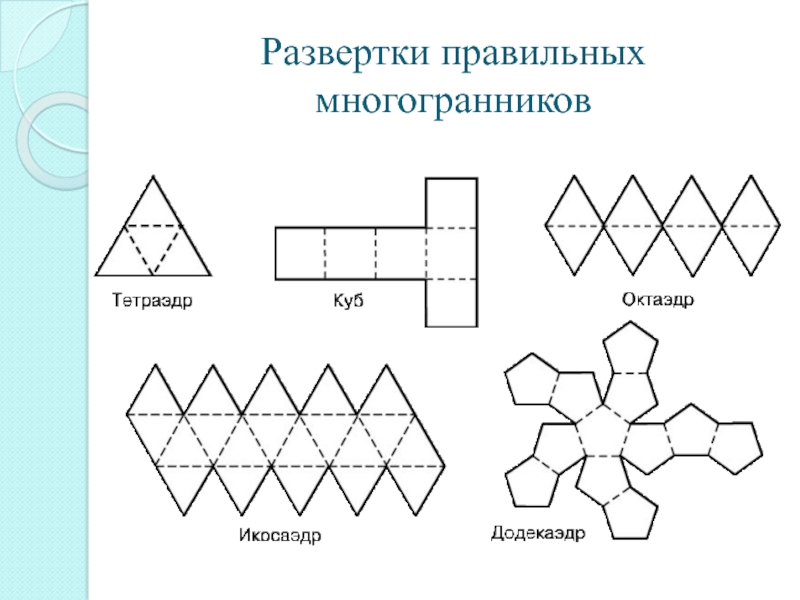
- 16. Развертки правильных многогранников
- 17. Свойства этих многогранников изучали ученые и священники,
- 18. Великий древнегреческий философ Платон, живший в IV
- 19. тетраэдр-огонь
- 20. куб-земля
- 21. октаэдр-воздух
- 22. икосаэдр-вода
- 23. додекаэдр-вселенная
- 24. Многогранники в природе04.03.2009
- 25. «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая мою геометрию»
- 26. Создания природы красивы и симметричны. В кристаллографии существует раздел, который называется «геометрическая кристаллография»
- 27. Кристалл поваренной солиКристаллическая решетка поваренной соли имеет кубическую структуру.
- 28. Кристаллы в форме октаэдраКвасцыШпинельФлюоритАлмаз
- 29. Кристаллы в форме призмРубинГорный хрусталь
- 30. Минерал куприт образует кристаллы в форме октаэдров.Минерал сильвин также имеет кристаллическую решетку в форме куба.
- 31. Скелет одноклеточного организма феодарии (Circogonia icosahedra) по
- 32. Икосаэдр оказался в центре внимания
- 33. Вирусы-бактериофагиГоловка вируса-бактериофага также имеет форму икосаэдра
- 34. Художники о правильных многогранникахСальвадор Дали «Тайная вечеря»,
- 35. В эпоху Возрождения большой интерес к формам
- 36. Геометрические тела в архитектуре 7 чудес света
- 37. Пирамида ХеопсаСреди египетских пирамид особое место занимает
- 38. Храм Артемиды
- 39. Статуя Зевса в Олимпии
- 40. Александрийский маяк
- 41. Колосс Родосский
- 42. Мавзолей в Галикарнасе
- 43. Вися́чие сады́ Семирами́ды
- 44. Полуправильные многогранники Полуправильные многогранники
- 45. Существует 13 полуправильных многогранников: Кубооктаэдр Икосододекаэдр
- 46. Ромбододекаэдр. (полуправильные тела)Он образован помощью семи кубов, образующих пространственный "крест« и додекаэдра.
- 47. Теорема Эйлера: Число вершин - число ребер
- 48. Итак, мы рассмотрели где встречаются правильные многогранники,
- 49. Скачать презентанцию
Цели:Познакомиться с новым типом многогранников - правильными многогранниками.Рассмотреть влияние правильных многогранников на возникновение философских теорий и гипотез.Рассмотреть связь геометрии и природы.
Слайды и текст этой презентации
Слайд 2Цели:
Познакомиться с новым типом многогранников - правильными многогранниками.
Рассмотреть влияние правильных
многогранников на возникновение философских теорий и гипотез.
Рассмотреть связь геометрии и
природы.Слайд 3« Правильных многогранников вызывающе мало, но этот весьма скромный по
численности отряд сумел пробраться в самые глубины различных наук».
Льюис КэроллСлайд 4Определение правильного многогранника
Многогранник называется правильным, если все его грани –
равные между собой правильные многоугольники, из каждой вершины выходит одинаковое
число ребер и все двугранные углы равныСлайд 5С глубокой древности человеку известны пять удивительных многогранников
Не существует правильного
многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n-угольники
при n≥6.Слайд 6Тетраэдр
Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр –
правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой
правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребраУ него 4 вершины,4 грани,6 ребер
Сумма плоских углов при каждой вершине равна 180 градусов
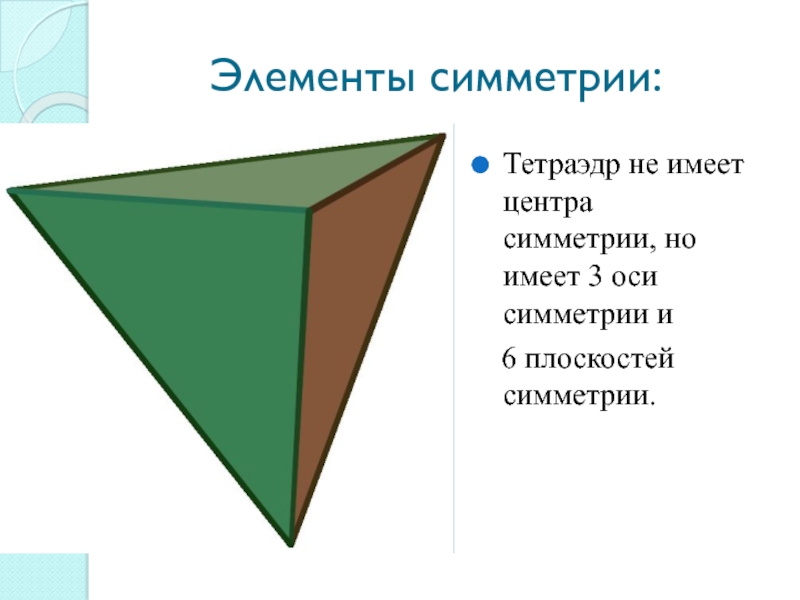
Слайд 7Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет 3
оси симметрии и
6 плоскостей симметрии.
Слайд 8Гексаэдр(куб)
Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все
грани которого – квадраты, и из каждой вершины выходит три
ребра.У него 6 граней,8 вершин,12 ребер
Сумма плоских углов при каждой вершине равна 270 градусов
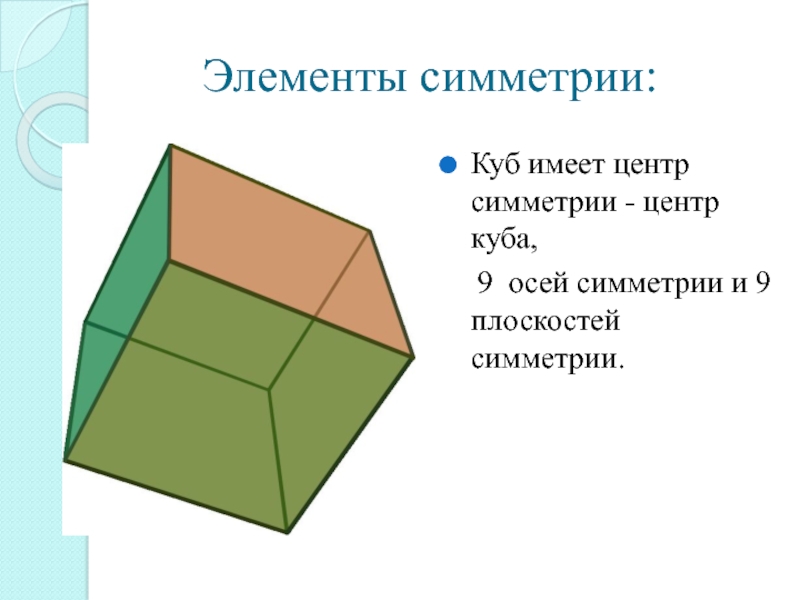
Слайд 9Элементы симметрии:
Куб имеет центр симметрии - центр куба,
9 осей симметрии и 9 плоскостей симметрии.
Слайд 10Октаэдр
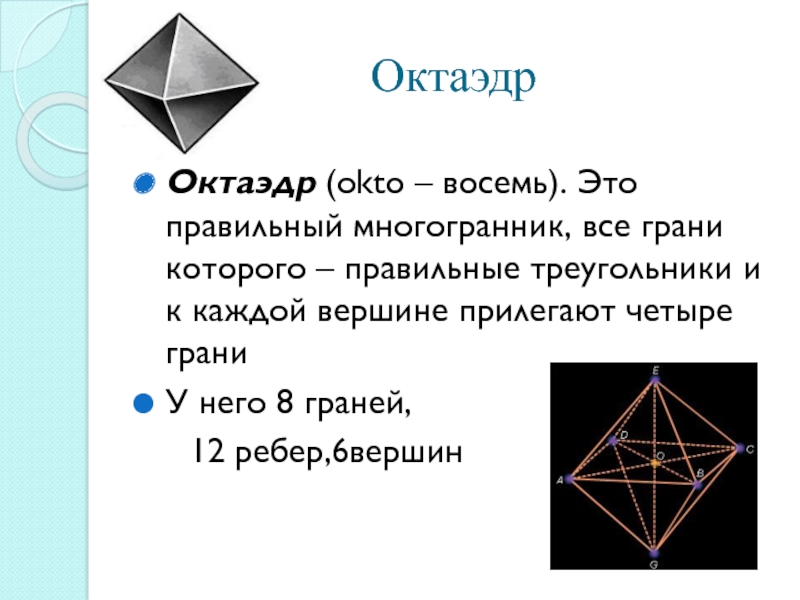
Октаэдр (okto – восемь). Это правильный многогранник, все грани которого
– правильные треугольники и к каждой вершине прилегают четыре грани
У него 8 граней,
12 ребер,6вершин
Слайд 11Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра, 9
осей симметрии и 9 плоскостей симметрии.
Слайд 12Додекаэдр
Существует правильный многогранник, у которого все грани правильные пятиугольники и
из каждой вершины выходит 3 ребра. Этот многогранник имеет 12
граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать).Сумма плоских углов при каждой вершине равна 324 градуса
Слайд 13Элементы симметрии:
Додекаэдр имеет центр симметрии - центр додекаэдра, 15
осей симметрии и 15 плоскостей симметрии.
Слайд 14Икосаэдр
Существует правильный многогранник, у которого все грани – правильные треугольники,
и из каждой вершины выходит 5 ребер. Этот многогранник имеет
20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать).Сумма плоских углов при каждой вершине равна 300 градусов
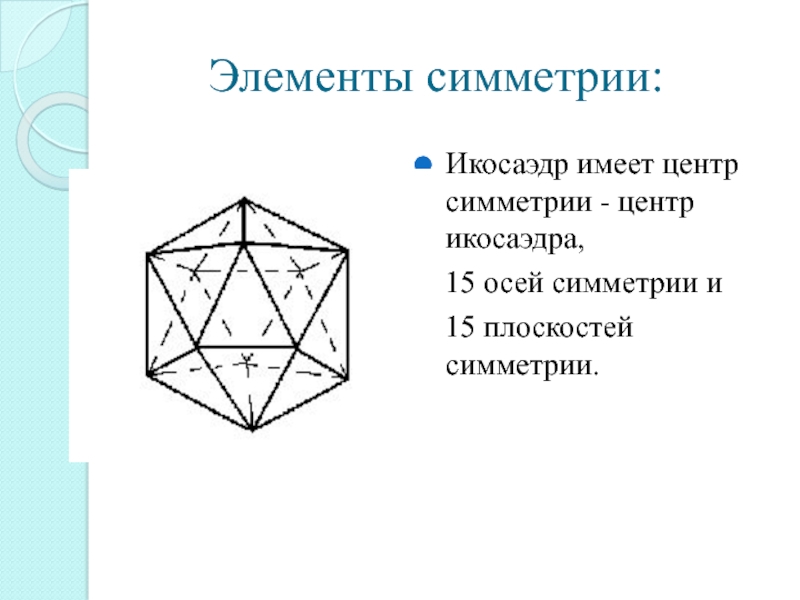
Слайд 15Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра,
15 осей симметрии и
15 плоскостей
симметрии.Слайд 17Свойства этих многогранников изучали ученые и священники, их модели можно
было увидеть в работах архитекторов и ювелиров, им приписывались различные
магические и целебные свойстваСлайд 18Великий древнегреческий философ Платон, живший в IV – V вв.
до нашей эры, считал, что эти тела олицетворяют сущность природы.
Четыре
сущности природы были известны человечеству: огонь, вода, земля и воздух.По мнению Платона, их атомы имели вид правильных многогранников.
Слайд 25«Мой дом построен по законам самой строгой архитектуры. Сам Евклид
мог бы поучиться, познавая мою геометрию»
Слайд 26Создания природы красивы и симметричны. В кристаллографии существует раздел, который
называется «геометрическая кристаллография»
Слайд 30Минерал куприт образует кристаллы в форме октаэдров.
Минерал сильвин также имеет
кристаллическую решетку в форме куба.
Слайд 31Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр.
Большинство феодарий живут на морской глубине и служат
добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник.Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности.
Это свойство помогает морскому организму преодолевать давление толщи воды.
Правильные многогранники в живой природе
Слайд 32 Икосаэдр оказался в центре внимания биологов в их
спорах относительно формы вирусов.
Вирус не может быть совершенно круглым,
как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр. Слайд 34Художники о правильных многогранниках
Сальвадор Дали «Тайная вечеря», на которой Христос
и его ученики изображены сидящими внутри огромного прозрачного додекаэдра.
Слайд 35В эпоху Возрождения большой интерес к формам правильных многогранников проявили
скульпторы. Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) ,
в известной гравюре''Меланхолия '‘ на переднем плане изобразил додекаэдр.
Слайд 37Пирамида Хеопса
Среди египетских пирамид особое место занимает пирамида фараона Хеопса.
Длина стороны её основания L =233,16 м; высота Н =146,6;
148,2 м.Слайд 44Полуправильные многогранники
Полуправильные многогранники или Архимедовы тела —
выпуклые многогранники, обладающие двумя свойствами:
1) Все грани являются правильными
многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник); 2) Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности все многогранные углы при вершинах конгруэнтны.
Слайд 45Существует 13 полуправильных многогранников:
Кубооктаэдр
Икосододекаэдр
Усеченный тетраэдр
Усечённый куб
Усечённый октаэдр
Усечённый додекаэдр
Усечённый икосаэдр
Ромбокубооктаэдр
Ромбоусечённый кубоктаэдр
Ромбоикосододекаэдр
Ромбоусечённый икосододекаэдр
Курносый куб
Курносый додекаэдр
Слайд 46Ромбододекаэдр.
(полуправильные тела)
Он образован помощью семи кубов, образующих пространственный "крест« и
додекаэдра.
Слайд 47Теорема Эйлера:
Число вершин - число ребер + число граней
=2
Один из величайших математиков мира, работы которого оказали решающее влияние
на развитие многих современных разделов математики.Л.Эйлер
(1707-1783)
Слайд 48Итак, мы рассмотрели где встречаются правильные многогранники, какими они бывают.
Математика
владеет не только истиной, но и высшей красотой - красотой
отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.Бертран Рассел.