Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Народная мудрость и свойства функции
Содержание
- 1. Народная мудрость и свойства функции
- 2. Три пути ведут к знаниям:путь размышления и
- 3. История возникновения функцииЛюди впервые поняли, что окружающие их явления взаимосвязаны
- 4. История возникновения функцииНачиная с XVII в. одним
- 5. История возникновения функцииЧёткого представления понятия функции в
- 6. История возникновения функции Слово «функция» (от
- 7. История возникновения функции«… Когда некоторые количества зависят
- 8. История возникновения функцииБольцано Бернард (1781-1848 гг.)Чешский математик,
- 9. Русский математик. Создатель (1826) неевклидовой геометрии. Дал
- 10. История возникновения функции Зависимость переменной y
- 11. Функции – это математические портреты устойчивых закономерностей,
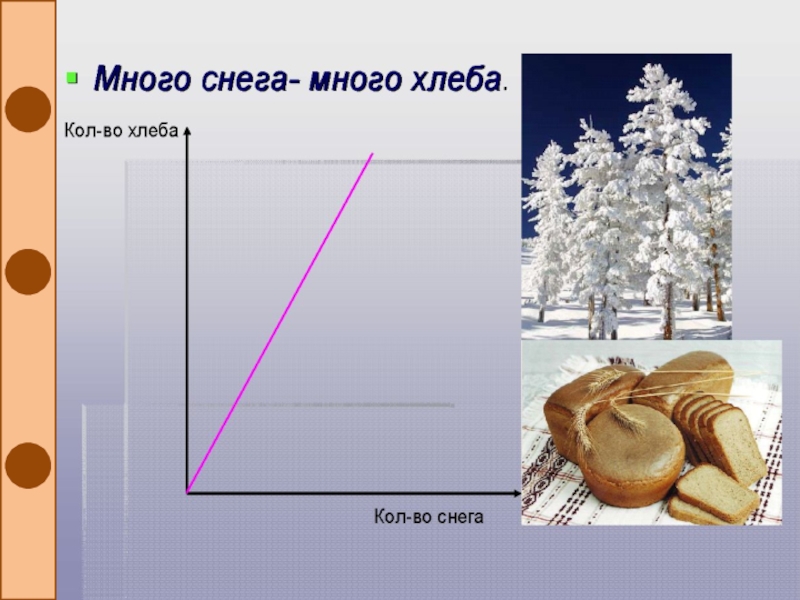
- 12. Свойства функции в пословицах и поговоркахФункция y=
- 13. «Чем дальше в лес, тем больше
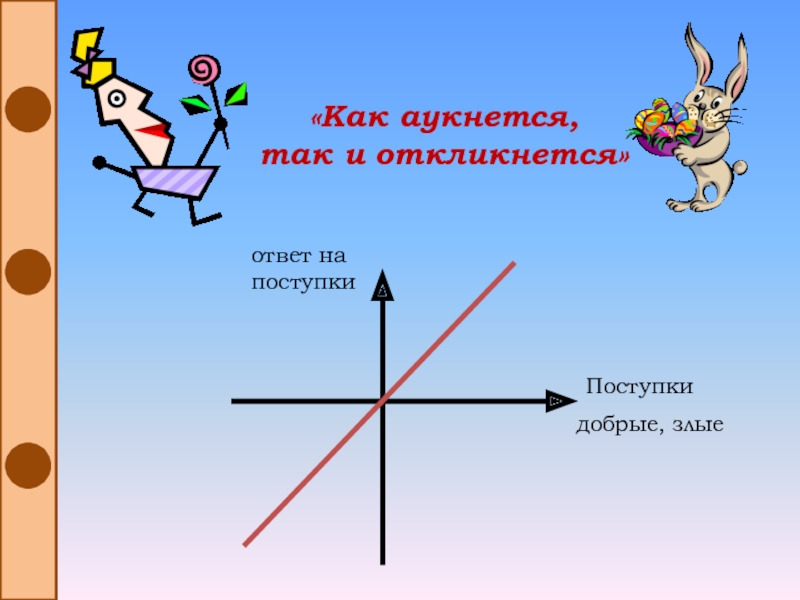
- 14. «Как аукнется, так и откликнется»ответ на поступки Поступкидобрые, злые
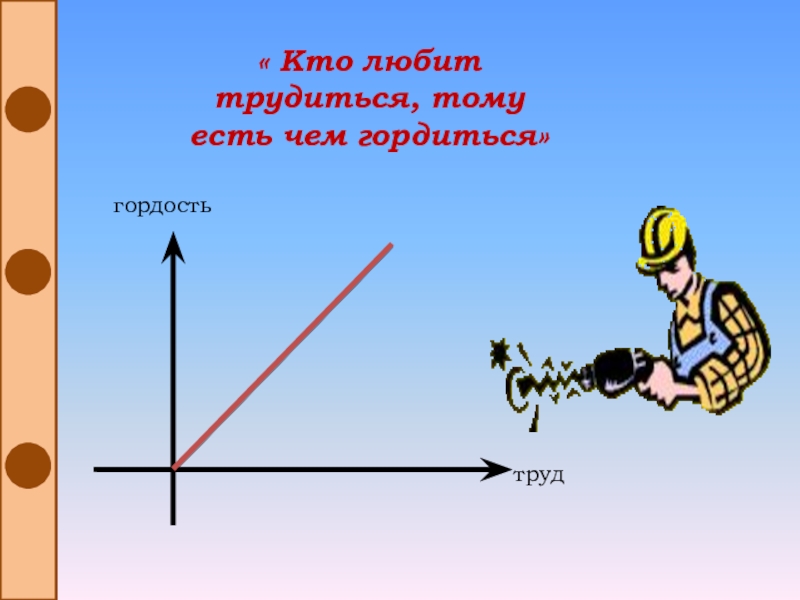
- 15. « Кто любит трудиться, тому есть чем гордиться»гордостьтруд
- 16. «Без труда не вынешь и рыбки из пруда»Х-количество затраченного трудаУ-количество полученного продукта
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Графиками функций, выражающие эти пословицы и поговорки являются графики прямой пропорциональной зависимости : y=kx+b.
- 21. Свойства функции в пословицах и поговорках2.Неубывающая функцияЕсли
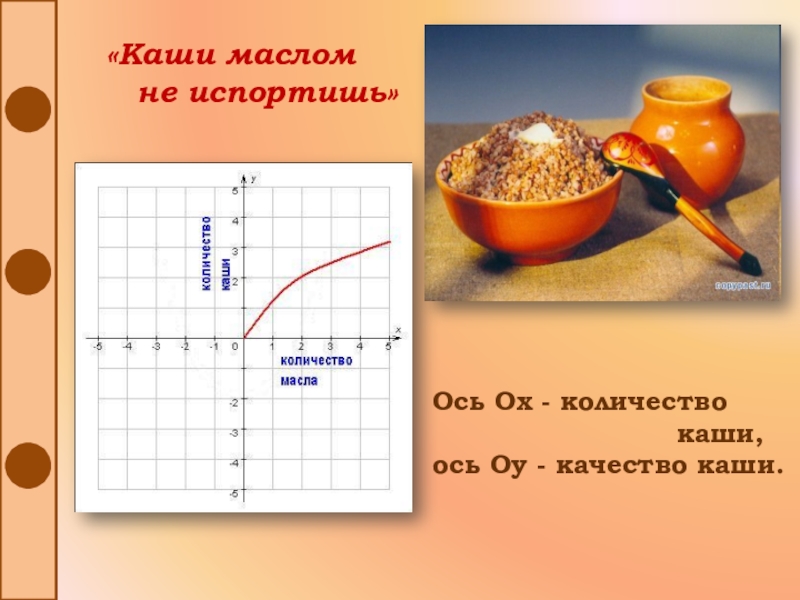
- 22. «Каши маслом не испортишь»Ось
- 23. Свойства функции в пословицах и поговорках3. Убывающая
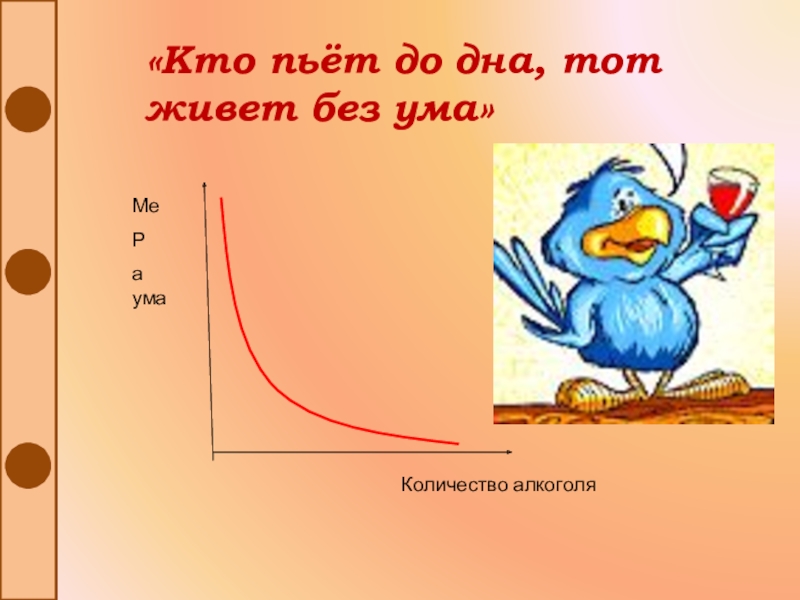
- 24. «Кто пьёт до дна, тот живет без ума»
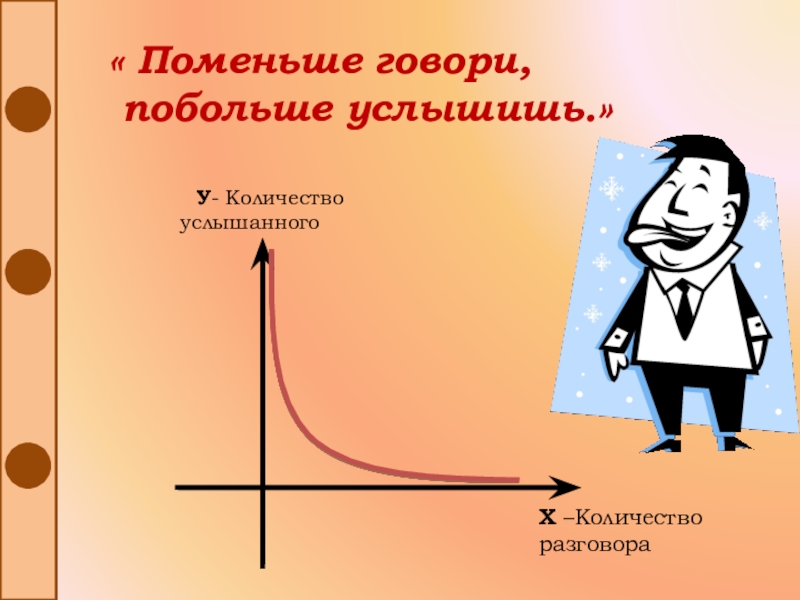
- 25. « Поменьше говори, побольше услышишь.» У- Количество услышанногоХ –Количество разговора
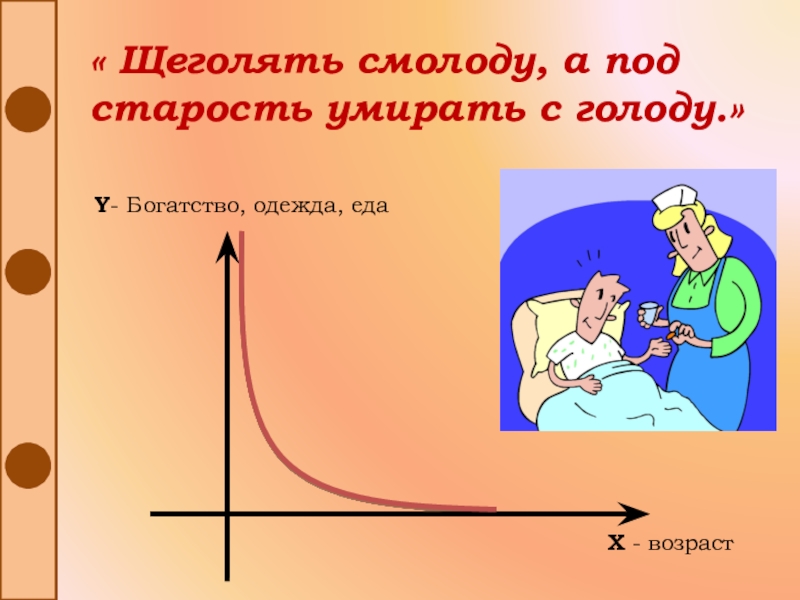
- 26. « Щеголять смолоду, а под старость умирать с голоду.» Y- Богатство, одежда, едаX - возраст
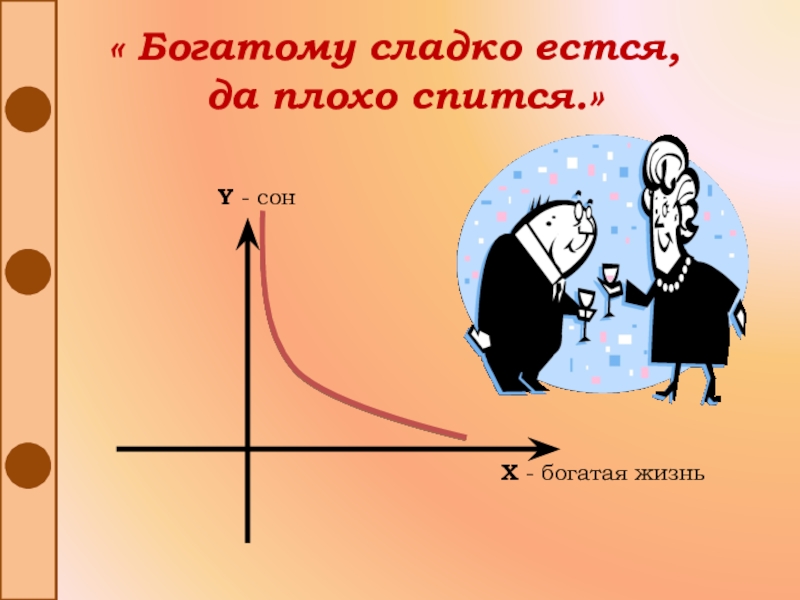
- 27. « Богатому сладко естся, да плохо спится.»
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. В этих народных высказываниях проявляется обратная
- 32. Свойства функции в пословицах и поговорках4.Ограниченные функции.Функция
- 33. Свойства функции в пословицах и поговорках5. Максимум
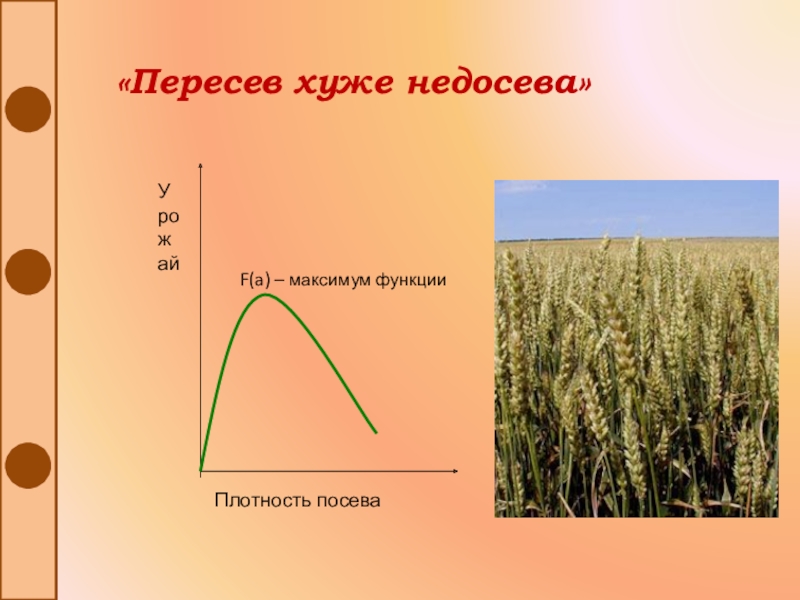
- 34. «Пересев хуже недосева»
- 35. Свойства функции в пословицах и поговорках6. Вогнутость
- 36. Свойства функции в пословицах и поговорках7. ПериодичностьФункция
- 37. «Долго думал, да ничего больше не выдумал.»
- 38. «Ума палата , да денег не гроша.»
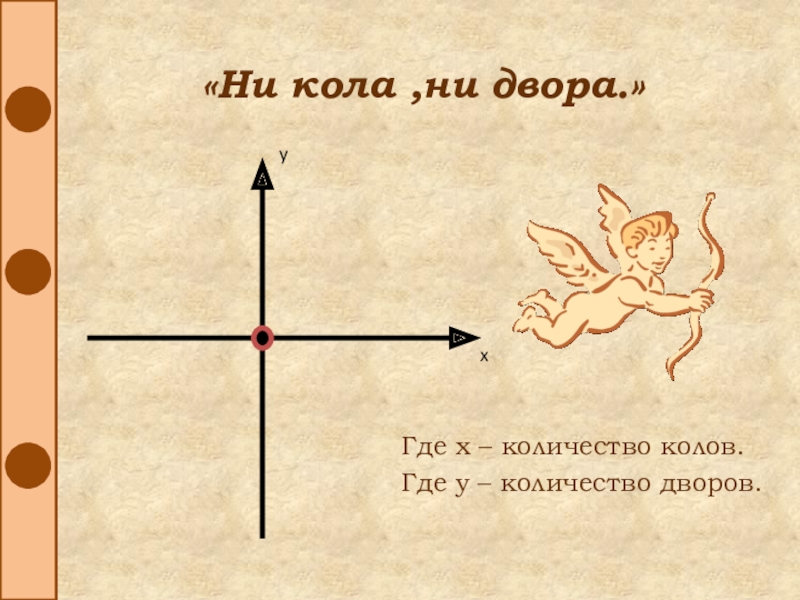
- 39. «Ни кола ,ни двора.»Где х – количество колов.Где у – количество дворов.
- 40. «Ни дров, ни лучины, а живёт без кручины.»
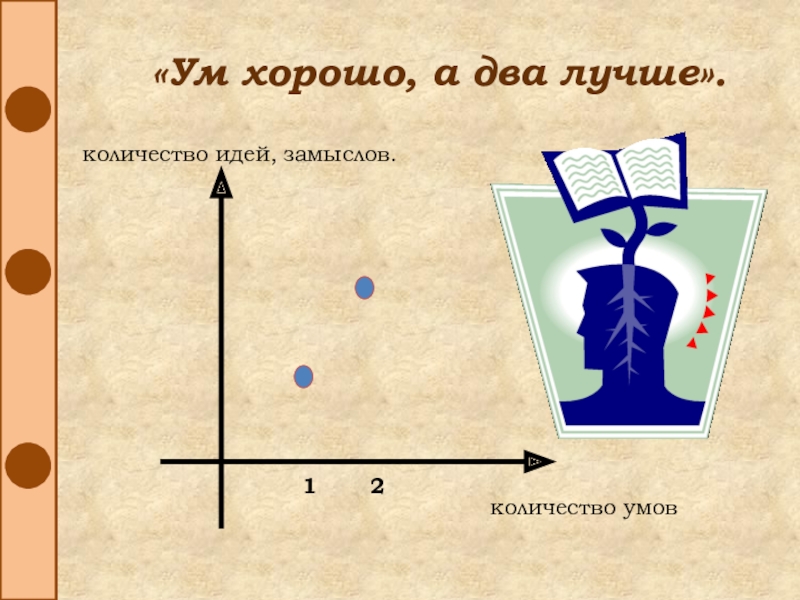
- 41. «Ум хорошо, а два лучше».2
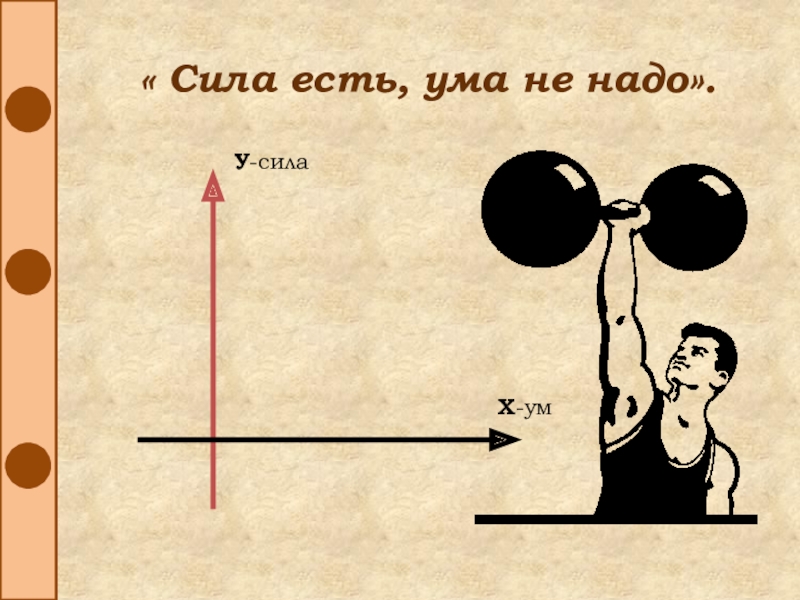
- 42. « Сила есть, ума не надо».
- 43. «Светит, да не греет.»Х-количество света.
- 44. Заключение У русского
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Три пути ведут к знаниям:
путь размышления и исследования
самый благородный;
путь подражания самый легкий;
путь опыта самый горький!
Слайд 4История возникновения функции
Начиная с XVII в. одним из важнейших понятий
является понятие функции.
Идея функциональной зависимости восходит к древности,
она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур.Явное и сознательное применение понятия функции и систематическое изучение функциональной зависимости берут своё начало в XVII в. в связи с проникновением в математику идеи переменных.
Слайд 5История возникновения функции
Чёткого представления понятия функции в XVII в. ещё
не было, однако путь к первому такому определению проложил Декарт,
который систематически рассматривал в своей «Геометрии» лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Декарт Рене (1596-1650 гг.)
Французский философ, математик, физик. Он является одним из основоположников аналитической геометрии. В его главном математическом труде «Геометрия» (1637) впервые введено понятие переменной величины, создан метод координат (декартовы координаты), введены общепринятые теперь значки для переменных величин (x,y,z,...) буквенных коэффициентов (a,b,c,...), степеней (x3, a5,...).
Слайд 6История возникновения функции
Слово «функция» (от латинского functio –
совершение, выполнение) Лейбниц употреблял с 1673 г. в смысле роли
(величина, выполняющая ту или иную функцию).Как термин - выражение «функция от x» стало употребляться Лейбницем и И. Бернулли.
«Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Лейбниц Готфрид Вильгельм
(1646-1716 гг.)
Немецкий математик, физик, философ, изобретатель, историк, языковед. В математике его важнейшей заслугой является разработка дифференциального и интегрального исчисления.
Бернулли Иоганн (1667-1748 гг.)
Швейцарский математик. Был сотрудником Лейбница в разработке дифференциального и интегрального исчислений, в области которых им был сделан ряд открытий.
Слайд 7История возникновения функции
«… Когда некоторые количества зависят от других таким
образом, что при изменении последних и сами они подвергаются изменению,
то первые называются функциями вторых».Определение Л. Эйлера гласит:
« Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств».
Эйлер Леонард (1707-1783 гг.)
Математик, физик, механик, астроном. Родился в Швейцарии. Более 30 лет работал в Петербургской АН. Список его трудов содержит около 850 названий, в их числе несколько многотомных монографий по всем основным разделам современной ему математике и ее приложениям. Заложил основы нескольких математических дисциплин.
«Функция есть кривая, начертанная свободным влечением руки».
Л.Эйлер, 1748.
Слайд 8История возникновения функции
Больцано Бернард (1781-1848 гг.)
Чешский математик, философ, теолог. Первым
(1817) выдвинул идею арифметической теории действительного числа. В его сочинениях
можно найти ряд фундаментальных понятий и теорем анализа, обычно связываемых с более поздними исследованиями других математиков.Даламбер Жан Лерон (1717-1783 гг.)
Французский математик, механик философ. Основные математические исследования относятся к теории обыкновенных дифференциальных уравнений.
Дирихле Петер Густав Лежен (1805-1859 гг.)
Немецкий математик. Основные труды по теории чисел и математическому анализу. Впервые точно сформулировал и исследовал понятие условной сходимости ряда (так называемый признак Дирихле), дал (1829) строгое доказательство возможности разложения в ряд Фурье функций, имеющей конечное число максимумов и минимумов.
Слайд 9Русский математик. Создатель (1826) неевклидовой геометрии. Дал (1834) метод приближенного
решения алгебраических уравнений высших степеней; внес значительный вклад в теорию
определителей. В области анализа Лейбниц получил новые результаты в теории тригонометрических рядов. Им же установлен один из наиболее удобных методов приближенного решения уравнений (метод Лобачевского).Лобачевский
Николай Иванович
(1792-1856 гг.)
История возникновения функции
Слайд 10История возникновения функции
Зависимость переменной y от переменной x
называется функцией, если каждому значению x соответствует единственное значение у.
Переменную x называют независимой переменной или аргументом, а переменную у – зависимой переменной.
Значение у, соответствующее заданному значению x, называют значением функции. Записывают: y =f(x)
Cимвол обозначения функции f изобрел в 1733 г. французский математик Клеро
В школьном учебнике «Алгебра» дано следующее определение :
Слайд 11Функции – это математические портреты устойчивых закономерностей, познаваемых человеком
Пословицы –
это отражение устойчивых закономерностей, выверенное многовековым опытом народа.
Находят ли
свойства функций отражение в народной мудрости? Слайд 12Свойства функции в пословицах и поговорках
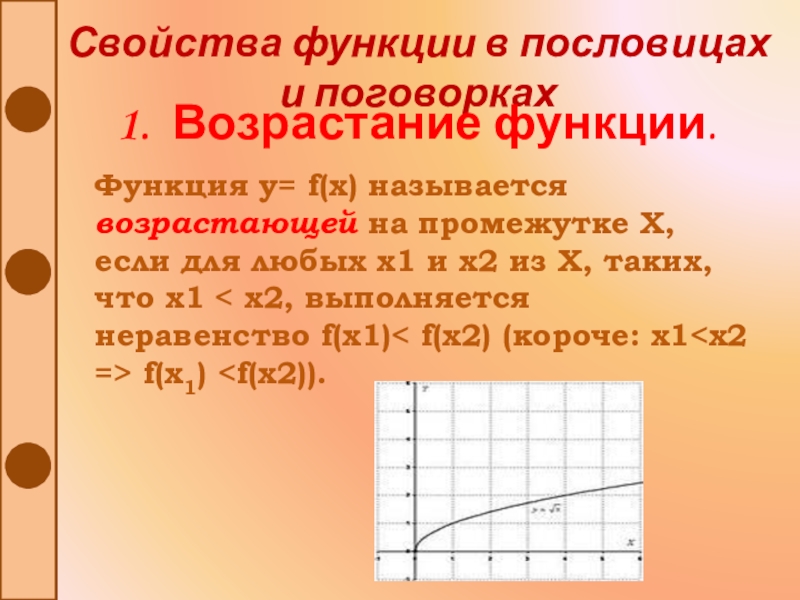
Функция y= f(x) называется возрастающей
на промежутке Х, если для любых х1 и х2 из
Х, таких, что х1 < х2, выполняется неравенство f(x1)< f(x2) (короче: x11. Возрастание функции.
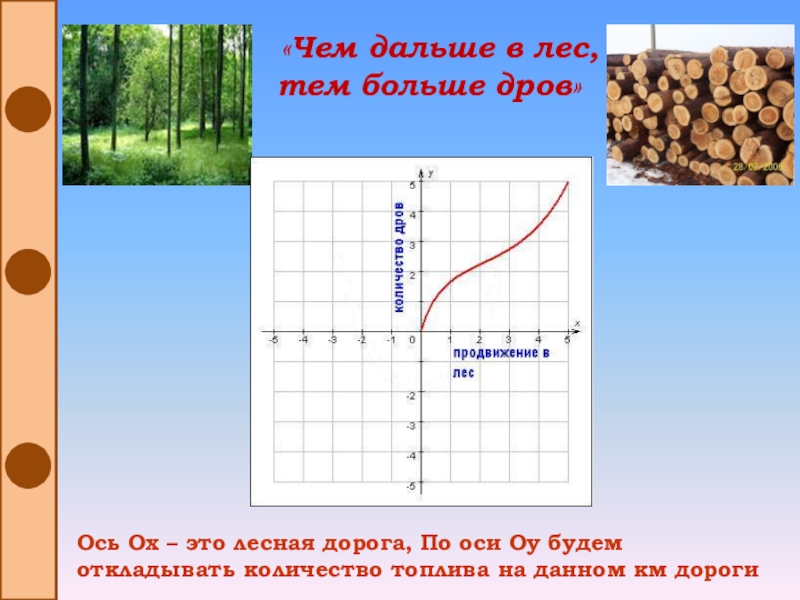
Слайд 13 «Чем дальше в лес,
тем больше дров»
Ось Ох
– это лесная дорога, По оси Оу будем откладывать количество
топлива на данном км дорогиСлайд 16«Без труда не вынешь и рыбки из пруда»
Х-количество затраченного
труда
У-количество полученного продукта
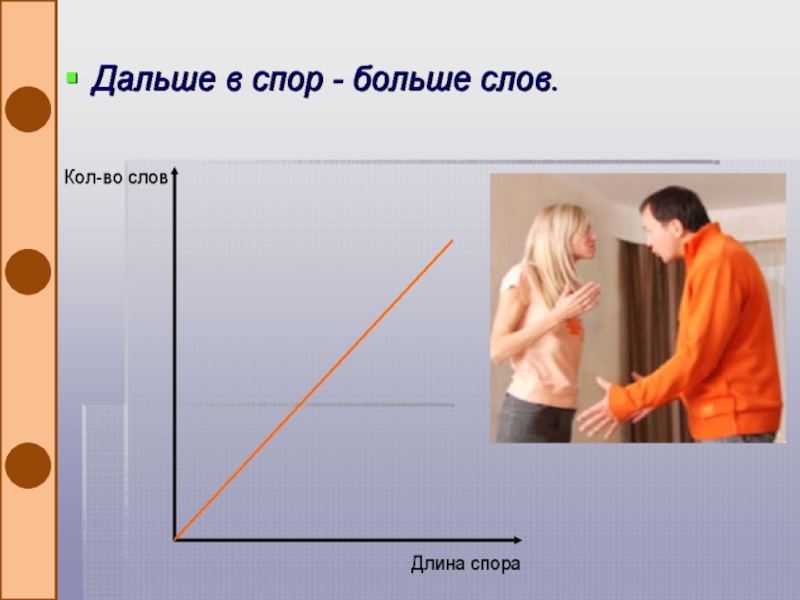
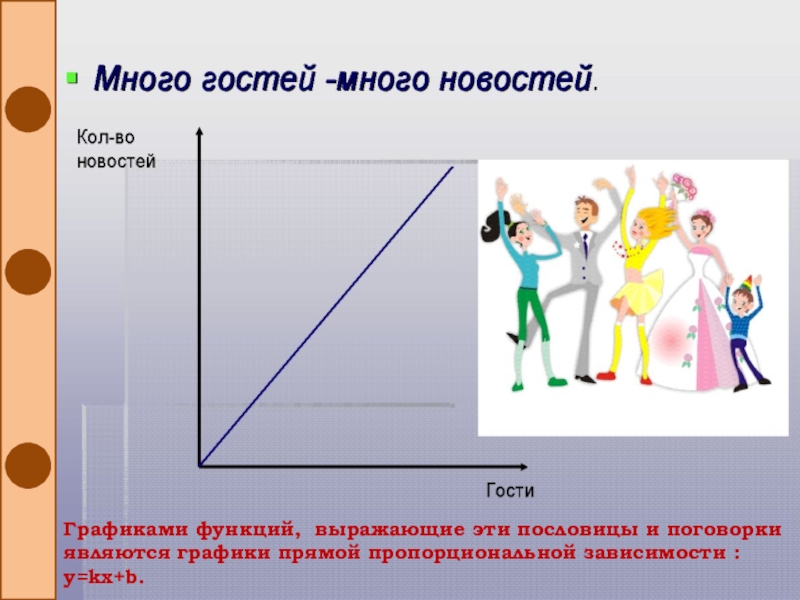
Слайд 20Графиками функций, выражающие эти пословицы и поговорки являются графики прямой
пропорциональной зависимости : y=kx+b.
Слайд 21Свойства функции в пословицах и поговорках
2.Неубывающая функция
Если для любых х1
и х2 из множества Х таких, что х1
f(x1) ≤ f(x2) , то функцию f(x) называют неубывающей на множестве Х.Слайд 23Свойства функции в пословицах и поговорках
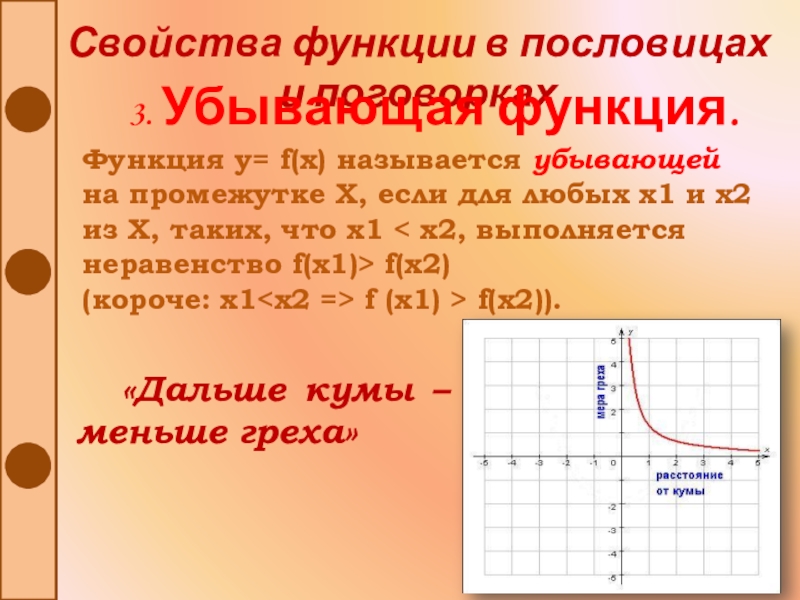
3. Убывающая функция.
Функция y= f(x)
называется убывающей на промежутке Х, если для любых х1 и
х2 из Х, таких, что х1 < х2, выполняется неравенство f(x1)> f(x2)(короче: x1
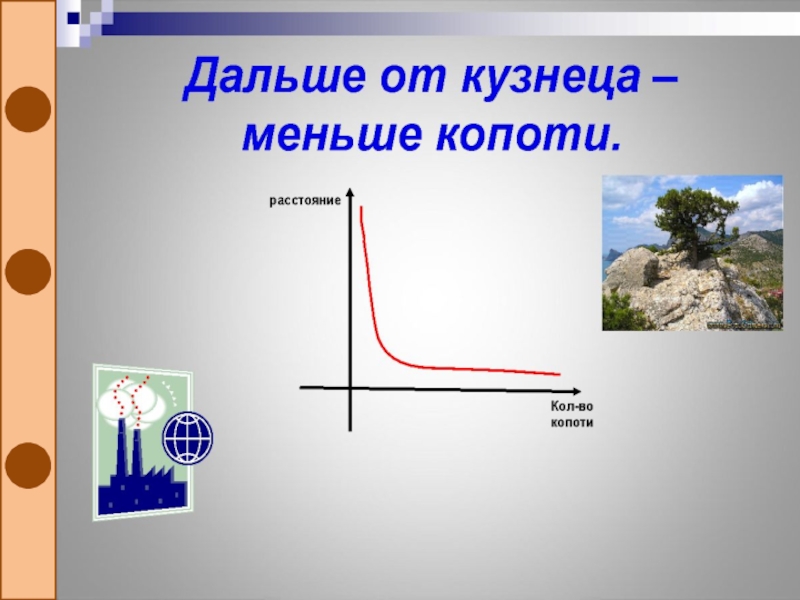
«Дальше кумы –меньше греха»
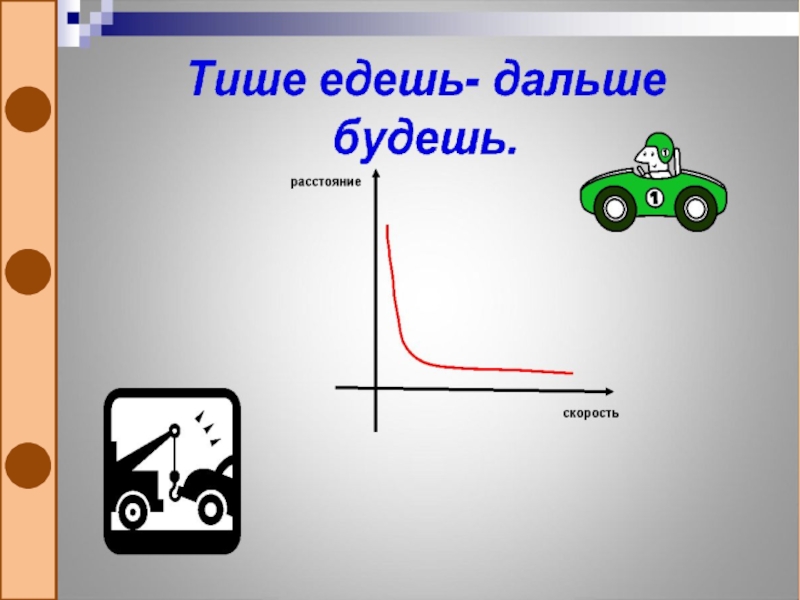
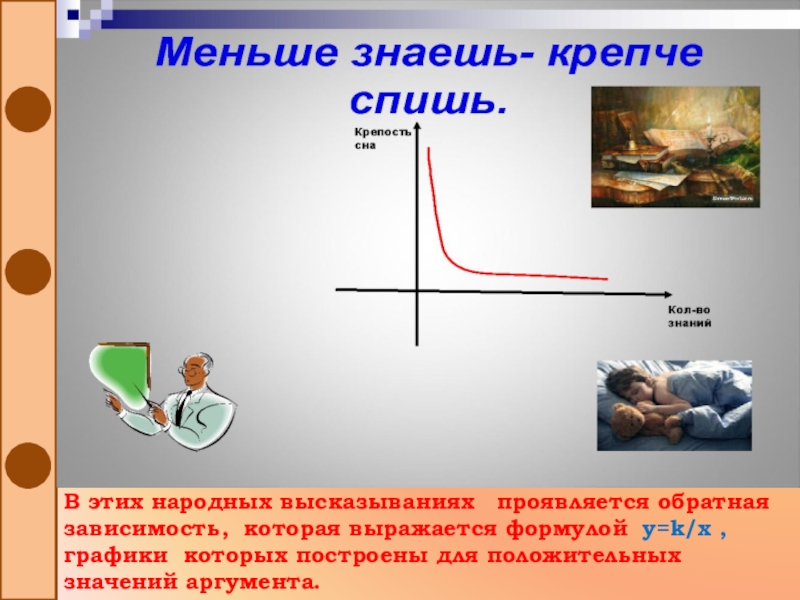
Слайд 31В этих народных высказываниях проявляется обратная зависимость, которая выражается
формулой y=k/x , графики которых построены для положительных значений аргумента.
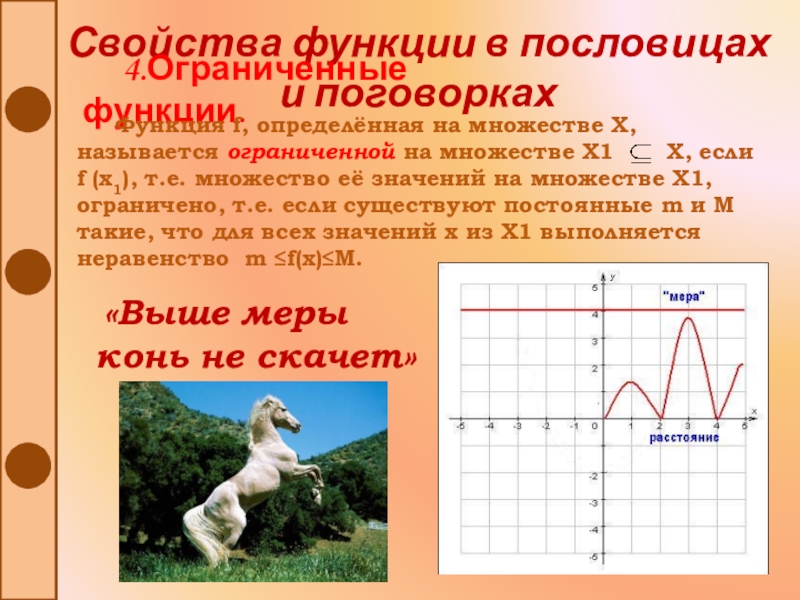
Слайд 32Свойства функции в пословицах и поговорках
4.Ограниченные функции.
Функция f, определённая на
множестве Х, называется ограниченной на множестве Х1
Х, если f (x1), т.е. множество её значений на множестве Х1, ограничено, т.е. если существуют постоянные m и M такие, что для всех значений x из Х1 выполняется неравенство m ≤f(x)≤M.
«Выше меры
конь не скачет»
Слайд 33Свойства функции в пословицах и поговорках
5. Максимум функции.
Пусть функция у
=f(x) определена в некоторой окрестности точки x0.
Функция у =f (x) имеет максимум в точке x0, если существует такая б – окрестность точки x0, что при x0 – б <х< x0 + б выполняется неравенство f (x) < f(x0),т.е. значение функции в этой точке больше, чем её значение во всех других точках, достаточно близких к x0.«Недосол на столе –
пересол на спине».
пересол
f(a)- максимум
Количество соли
Слайд 35Свойства функции в пословицах и поговорках
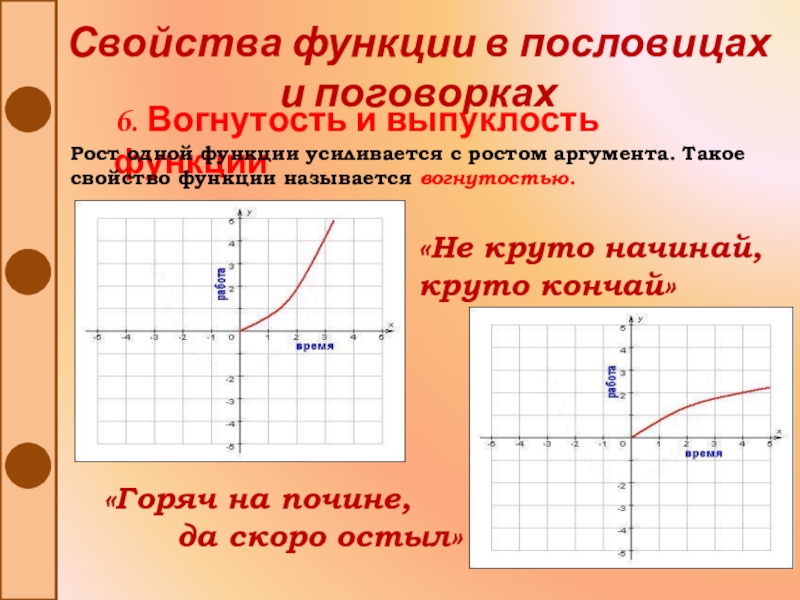
6. Вогнутость и выпуклость функции
«Не круто начинай,
круто кончай»
«Горяч на почине,
да скоро остыл»
Рост одной функции усиливается с ростом аргумента. Такое свойство функции называется вогнутостью.
Слайд 36Свойства функции в пословицах и поговорках
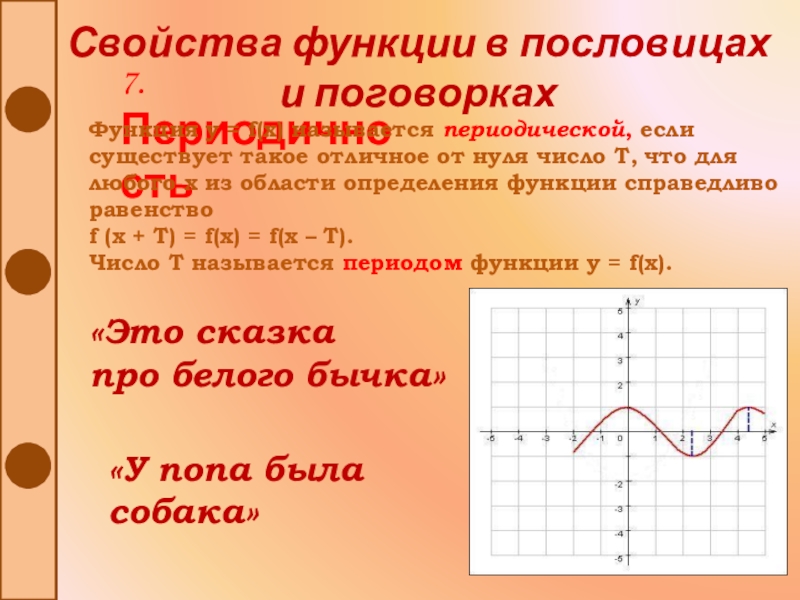
7. Периодичность
Функция y = f(x)
называется периодической, если существует такое отличное от нуля число Т,
что для любого x из области определения функции справедливо равенствоf (x + T) = f(x) = f(x – T).
Число Т называется периодом функции y = f(x).
«Это сказка
про белого бычка»
«У попа была
собака»
Слайд 44Заключение
У русского народа, как у
любого другого, существует бесчисленное множество пословиц и поговорок.
Они создавались и накапливались народом в течении многовековой его истории и отражали его жизнь, условия труда, культуру. Они отражают взаимосвязи, существующие между различными жизненными категориями (объектами). Т.е.фактически являются отражениями функциональных зависимостей и доказывают ,что
функция - это сама жизнь!