веками пытался
объяснить и создать порядок, красоту и
совершенство».
Герман ВейльА
А1
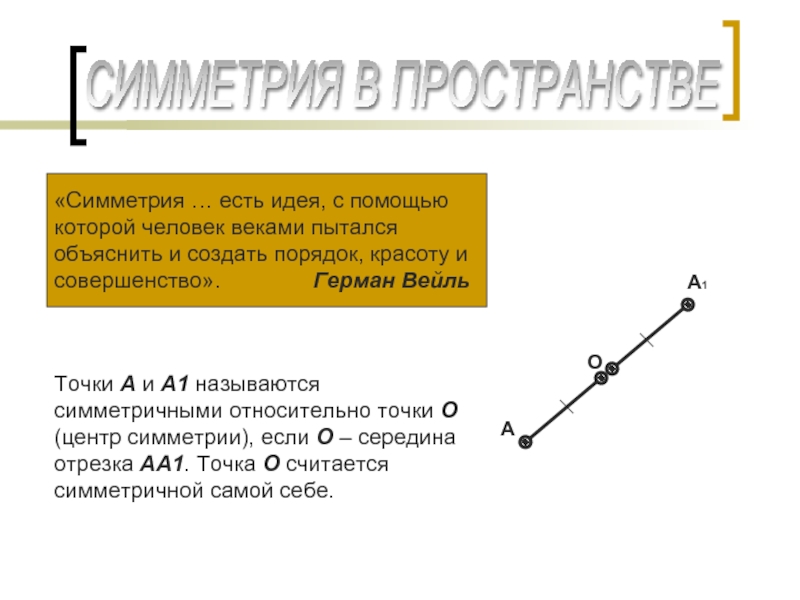
Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1. Точка О считается симметричной самой себе.