Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подобные треугольники
Содержание
- 1. Подобные треугольники
- 2. Цели урокавведение понятия подобных треугольников;развитие творческой деятельности;формирование
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
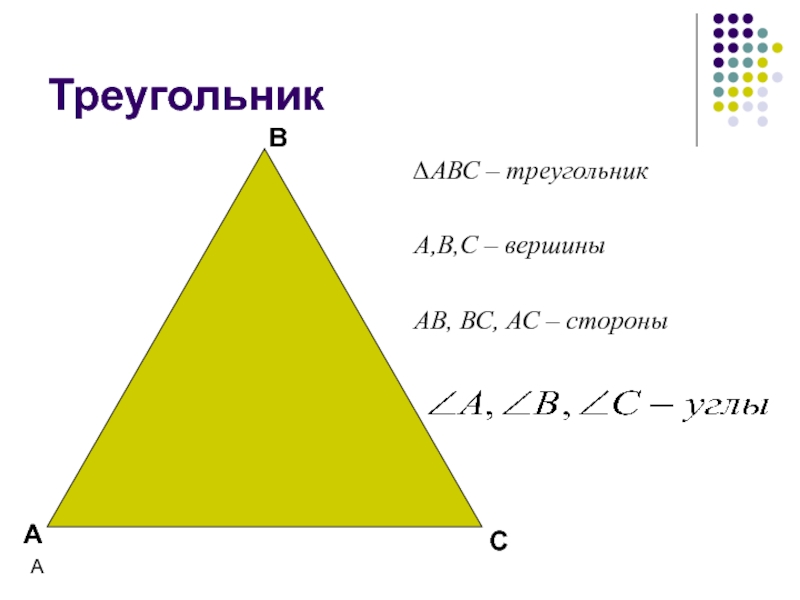
- 6. Треугольник
- 7. Слайд 7
- 8. Виды треугольников1234
- 9. Равнобедренный треугольник
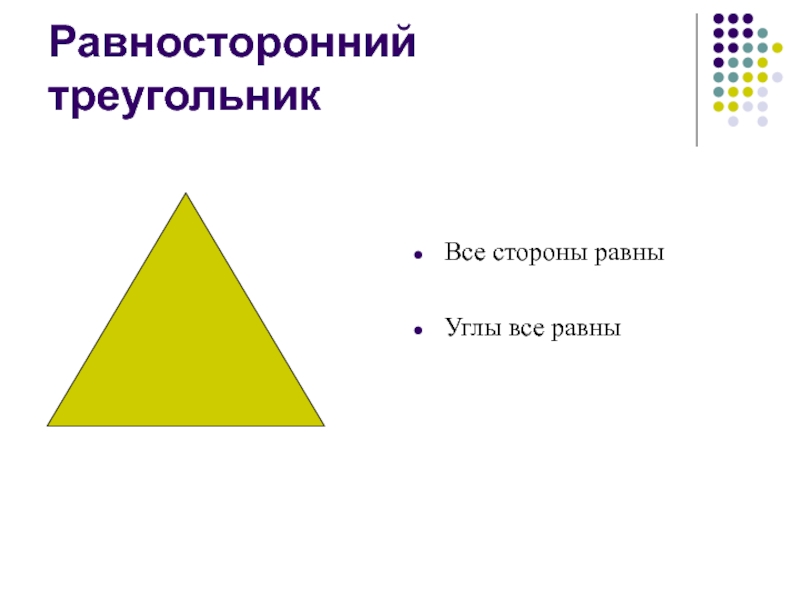
- 10. Равносторонний треугольник
- 11. Прямоугольный треугольник
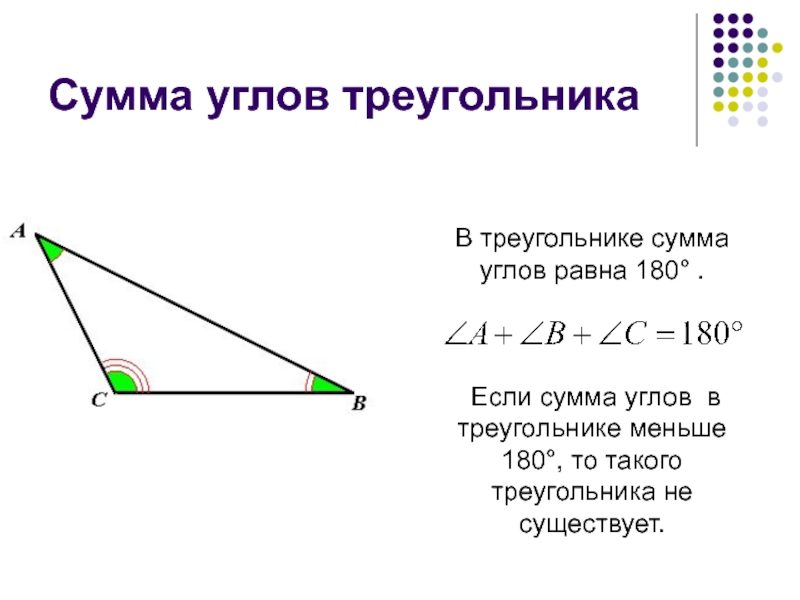
- 12. Сумма углов треугольникаВ треугольнике сумма углов равна
- 13. Признаки равенстваПо двум сторонам и углу между
- 14. ФАЛЕС
- 15. Пирамида ХеопсаФараон IV династии Хеопс воздвиг самую
- 16. «Подобные треугольники»
- 17. Работа с текстом учебника“+” – это я
- 18. Подобные фигуры
- 19. Слайд 19
- 20. Слайд 20
- 21. Как можно назвать эти фигуры?
- 22. Что из прочитанного оказалось неизвестным?
- 23. Укажите сходственные стороныACBHA1B1C1H1
- 24. Подобные треугольники – этоПохожие, одинаковые, пропорциональныеСходственные стороны:
- 25. Задача №1Дано: ∆АВС и ∆МNK
- 26. Укажите подобные фигуры
- 27. Домашнее задание:
- 28. Спасибо за урок
- 29. Скачать презентанцию
Цели урокавведение понятия подобных треугольников;развитие творческой деятельности;формирование умений задавать вопросы и строить цепочку логических рассуждений, выводов;формирование навыков работы с текстом, с новыми понятиям
Слайды и текст этой презентации
Слайд 2Цели урока
введение понятия подобных треугольников;
развитие творческой деятельности;
формирование умений задавать вопросы
и строить цепочку логических рассуждений, выводов;
с новыми понятиям
Слайд 3
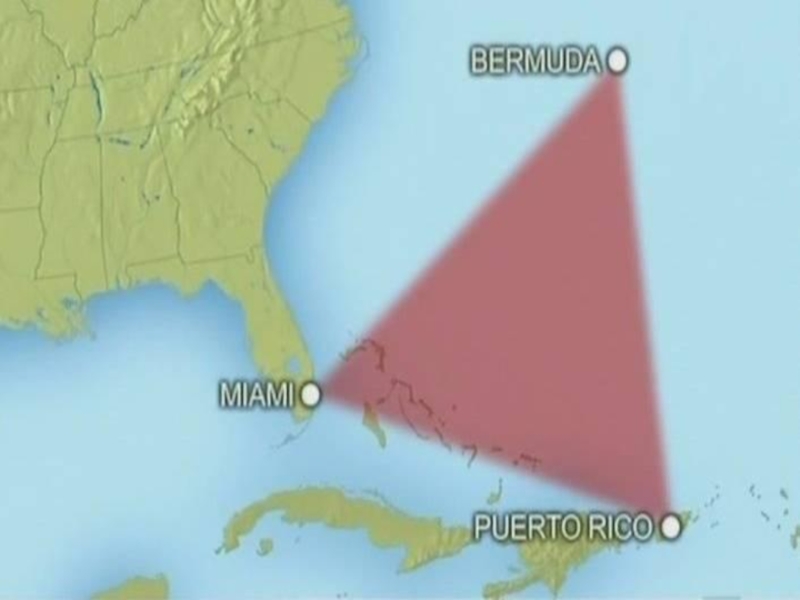
Бермудские острова, владение Великобритании в северо-западной части Атлантического океана, близ берегов Северной Америки.
Острова были открыты испанским мореплавателем Х. Бермудесом в 1522 г.
Слайд 4
Пуэрто-Рико, содружество Пуэрто-Рико, владение США в Вест-Индии, на острове Пуэрто-Рико и близ лежащих островах
Флорида, полуостров на юго-востоке Северной Америки, часть штата Флорида (США).
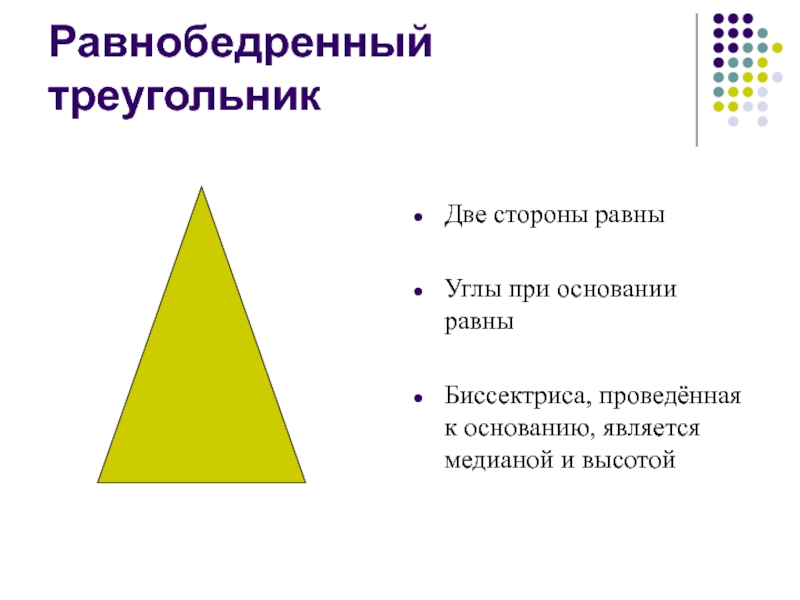
Слайд 9Равнобедренный треугольник
Две стороны равны
Углы при основании равны
Биссектриса, проведённая к основанию, является медианой и высотой
Слайд 11Прямоугольный треугольник
Один угол
прямойСумма двух острых углов равна 90°
Катет, лежащий против угла в 30° равен половине гипотенузы (а = с)
с² = а² + в²
S = а·в
90°
30°
с
а
в
Слайд 12Сумма углов треугольника
В треугольнике сумма углов равна 180° .
Если
сумма углов в треугольнике меньше 180°, то такого треугольника не
существует.
Слайд 13Признаки равенства
По двум сторонам и углу между ними
По стороне и
двум прилежащим к ней углам
По трём сторонам
Слайд 14ФАЛЕС
Древнегреческий учёный и философ, основатель ионийской(милетской) школы. Фалес первым стал доказывать геометрические теоремы.
Слайд 15Пирамида Хеопса
Фараон IV династии Хеопс воздвиг самую большую из египетских
пирамид, которая была самым высоким сооружением в течении последующих 4
тысячелетий (высота пирамиды – 146,6 м, длина каждой из сторон основания – 230 м). На постройку пирамиды Хеопса ушло около 2,3 миллиона каменных блоков весом до 2,5 т.
Слайд 17Работа с текстом учебника
“+” – это я знаю и согласен;
“
–” – в этом я сомневаюсь, не согласен;
“!” – это
интересно и ново, неожиданно;“?” – это непонятно, надо получить дополнительную информацию и объяснения учителя.
Слайд 24Подобные треугольники – это
Похожие, одинаковые, пропорциональные
Сходственные стороны:
АВ
и A1B1, ВС и B1C1, АС и A1C1
Равные углы: ∠A=∠A1,∠B=∠B1,∠C=∠C1
Сходственные
стороны пропорциональны:- коэффициент подобия
Δ АВС ~ Δ A1 B1 C1
Слайд 25Задача №1
Дано: ∆АВС и ∆МNK
4,ВС = 3, АС = 6
= 8, NК = 6, МК = 12Определите подобны ли треугольники?
Задача № 2
Дано: ∆АВС подобен ∆MNK
<А = 30°, <В = 85°, <С = 65°.
Создать по данным задачи модели подобных треугольников.
Слайд 27 Домашнее задание: 1. Всем: придумать способ измерения высоты
пирамиды. 2. Для 1 группы: подготовить рисунки или макеты подобных
фигур. 3. Для 2 группы: подготовить историческую справку о Фалесе Милетском.
