Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность прямых в пространстве
Содержание
- 1. Параллельность прямых в пространстве
- 2. ВСПОМНИМ ПЛАНИМЕТРИЮКаково может быть взаимное расположение двух прямых на плоскости?Какие прямые в планиметрии называются параллельными?
- 3. ВСПОМНИМ ПЛАНИМЕТРИЮАксиома параллельных прямых - ?Через точку,
- 4. ВСПОМНИМ ПЛАНИМЕТРИЮСледствия аксиомы параллельных прямых - ?Если
- 5. ВЕРНЕМСЯ В ПРОСТРАНСТВО.Каково может быть взаимное расположение
- 6. ВЕРНЕМСЯ В ПРОСТРАНСТВОКакие прямые в пространстве называются
- 7. Теорема о параллельных прямых.Через любую точку пространства,
- 8. …они лежат на параллельных прямыхОтрезки в пространстве
- 9. Лемма о параллельных прямыхЕсли одна из параллельных
- 10. Дано: Доказать: b и имеют общую точку, причем она единственнаяabЛемма о параллельных прямых
- 11. abсРМДано: Доказать: b и имеют общую точку, причем она единственнаяЛемма о параллельных прямых
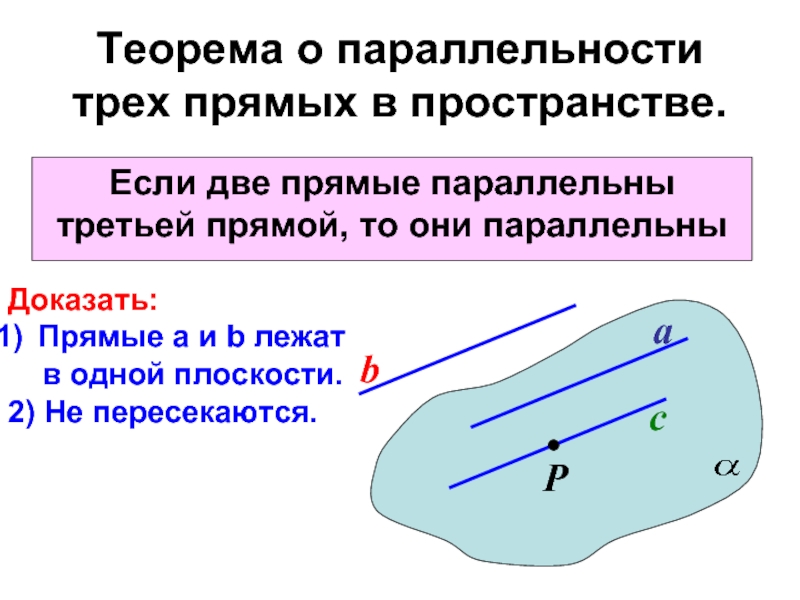
- 12. Теорема о параллельности трех прямых в пространстве.Если две прямые параллельны третьей прямой, то они параллельныabсДано:Доказать:и
- 13. Теорема о параллельности трех прямых в пространстве.Если
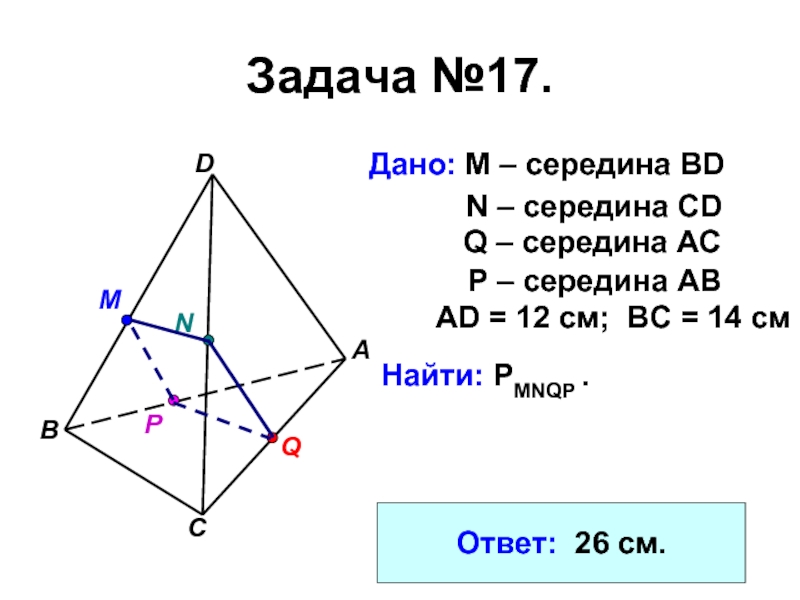
- 14. Задача №17.Дано: М – середина BD ABDCNMРQN
- 15. Скачать презентанцию
ВСПОМНИМ ПЛАНИМЕТРИЮКаково может быть взаимное расположение двух прямых на плоскости?Какие прямые в планиметрии называются параллельными?
Слайды и текст этой презентации
Слайд 2ВСПОМНИМ ПЛАНИМЕТРИЮ
Каково может быть взаимное расположение двух прямых на плоскости?
Какие
прямые в планиметрии называются параллельными?
Слайд 3ВСПОМНИМ ПЛАНИМЕТРИЮ
Аксиома параллельных прямых - ?
Через точку, не лежащую на
данной прямой,
проходит прямая, параллельная данной и притом только одна
Слайд 4ВСПОМНИМ ПЛАНИМЕТРИЮ
Следствия аксиомы параллельных прямых - ?
Если прямая пересекает одну
из параллельных прямых, то она пересекает и другую.
Если две прямые
параллельны третьей прямой, то они параллельны.Слайд 5ВЕРНЕМСЯ В ПРОСТРАНСТВО.
Каково может быть взаимное расположение прямых в пространстве?
А
B
C
D
А1
B1
C1
D1
AB
и CD
B1C и C1C
AD1 и A1D
BC и AA1
B1C и A1D
II
?
∩
?
∩
?
?
?
Слайд 6ВЕРНЕМСЯ В ПРОСТРАНСТВО
Какие прямые в пространстве называются параллельными?
А
B
C
D
А1
B1
C1
D1
B1C и A1D
Параллельными
называются прямые,
лежащие в одной
плоскости и не
имеющие точек
пересечения.
Слайд 7Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная данной, и притом только одна.
К
a
b
Слайд 8…они лежат на параллельных прямых
Отрезки в пространстве называются параллельными, если
…
Лучи в пространстве называются параллельными, если …
Параллельные отрезки,
параллельные лучи
в пространстве.
Слайд 9Лемма о параллельных прямых
Если одна из параллельных прямых пересекает плоскость,
то и вторая прямая также пересекает эту плоскость?
a
b
Слайд 11a
b
с
Р
М
Дано:
Доказать: b и имеют общую точку, причем
она единственная
Лемма о параллельных прямых
Слайд 12Теорема о параллельности трех прямых в пространстве.
Если две прямые параллельны
третьей прямой, то они параллельны
a
b
с
Дано:
Доказать:
и
Слайд 13Теорема о параллельности трех прямых в пространстве.
Если две прямые параллельны
третьей прямой, то они параллельны
a
b
с
Р
Доказать:
Прямые а и b лежат
в одной плоскости.2) Не пересекаются.
Слайд 14Задача №17.
Дано: М – середина BD
A
B
D
C
N
M
Р
Q
N – середина CD
Q
– середина АС
P – середина АВ
АD = 12 см; ВС
= 14 смНайти: PMNQP .
Ответ: 26 см.
Теги