Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллелепипед
Содержание
- 1. Параллелепипед
- 2. Параллелепипед Параллелепипед – этопризма, основанием которой является параллелограмм
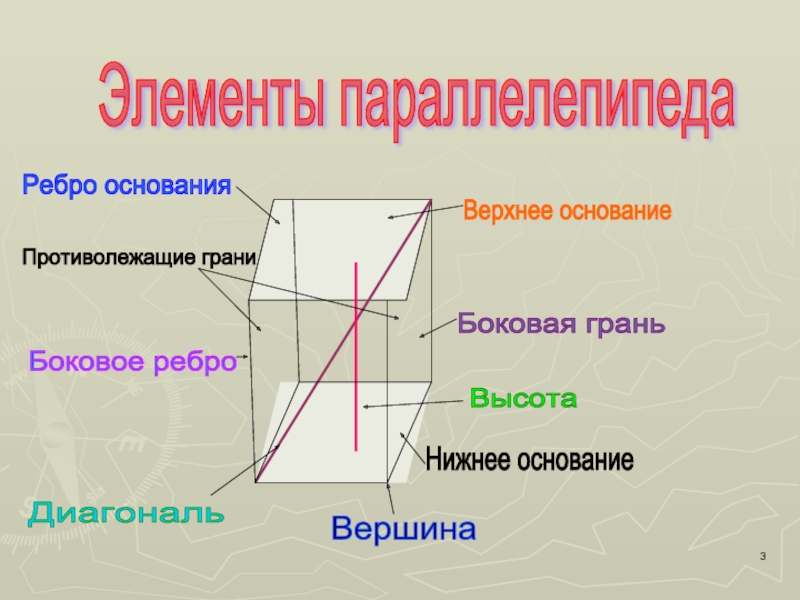
- 3. Элементы параллелепипеда Ребро основания Нижнее основание Верхнее
- 4. Свойства параллелепипеда У параллелепипеда все грани –
- 5. Виды параллелепипеда Наклонный Прямой Боковые рёбра перпендикулярны основаниюпрямоугольный Куб В основании лежит прямоугольникВсе грани - квадраты
- 6. Прямоугольный параллелепипед Это прямой параллелепипед, у которого
- 7. Куб Прямоугольный параллелепипед, у которого все рёбра равныS=6a2V=a3
- 8. Поверхность прямоугольного параллелепипеда S полн 2(ab+bc+ac) = Объём прямоугольного параллелепипеда V = abc
- 9. Сечения параллелепипеда Перпендикулярное Диагональное
- 10. презентация закончена
- 11. У параллелепипеда противолежащие грани параллельны и равныДано:
- 12. Диагонали параллелепипеда пересекаются в одной точке и
- 13. В прямоугольном параллелепипеде квадрат любой диагонали равен
- 14. Скачать презентанцию
Параллелепипед Параллелепипед – этопризма, основанием которой является параллелограмм
Слайды и текст этой презентации
Слайд 3Элементы параллелепипеда
Ребро основания
Нижнее основание
Верхнее основание
Боковая грань
Боковое ребро
Диагональ
Высота
Вершина
Противолежащие грани
Слайд 4Свойства параллелепипеда
У параллелепипеда все грани – параллелограммы
Основания параллелепипеда равны
Основания
параллелепипеда лежат в параллельных плоскостях
Боковые рёбра параллельны и равны
Противолежащие грани
параллельны и равныДиагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам
Слайд 5Виды параллелепипеда
Наклонный
Прямой
Боковые рёбра перпендикулярны основанию
прямоугольный
Куб
В
основании лежит прямоугольник
Все грани - квадраты
Слайд 6Прямоугольный параллелепипед
Это прямой параллелепипед, у которого основанием является прямоугольник
У
прямоугольного параллелепипеда все грани прямоугольники
Длины непараллельных рёбер прямоугольного параллелепипеда называются
его линейными размерами. У прямоугольного параллелепипеда три измерения
Квадрат диагонали равен сумме квадратов трех его измерений
Слайд 8Поверхность прямоугольного параллелепипеда
S
полн
2(ab+bc+ac)
=
Объём прямоугольного параллелепипеда
V = abc
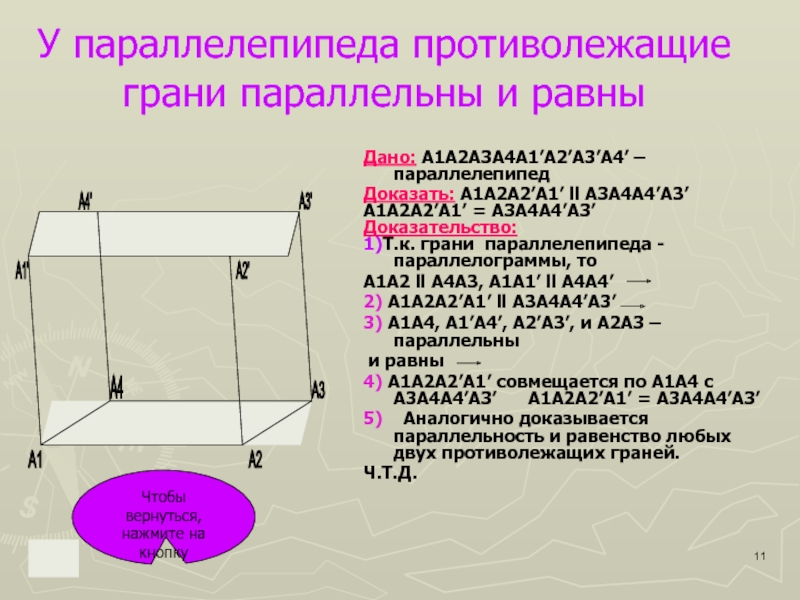
Слайд 11У параллелепипеда противолежащие грани параллельны и равны
Дано: A1A2A3A4A1’A2’A3’A4’ – параллелепипед
Доказать:
A1A2A2’A1’ ll А3А4A4’A3’
A1A2A2’A1’ = А3А4A4’A3’
Доказательство:
1)Т.к. грани параллелепипеда -
параллелограммы, тоА1А2 ll A4A3, A1A1’ ll A4A4’
2) A1A2A2’A1’ ll А3А4A4’A3’
3) A1A4, A1’A4’, A2’A3’, и A2A3 – параллельны
и равны
4) A1A2A2’A1’ совмещается по А1А4 с А3А4А4’A3’ A1A2A2’A1’ = А3А4A4’A3’
5) Аналогично доказывается параллельность и равенство любых двух противолежащих граней.
Ч.Т.Д.
Чтобы вернуться, нажмите на кнопку
Слайд 12Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся
пополам
Дано: A1A2A3A4A1’A2’A3’A4’ – параллелепипед
А1А3’ и A4A2’ – диагонали, О –
точка пересечения диагоналей
Доказать: А1А3’ и A4A2’ пересекаются и точкой пересечения делятся пополам
Доказательство:
1) Т.к. А1А2А3А4 и А2А2’A3’A3
параллелограммы и А2А3 – общая, то А1А4 ll
А2’А3’ и лежат в одной плоскости (А1А4А3’А2’).
2) А1А4А3’А2’ пересекает плоскости противол. граней по
параллельным прямым А1А2 и А4А3’.
3) А1А4А3’А2’ – параллелограмм.
Диагонали параллелепипеда А1А3’ и A4A2’ –
диагонали этого параллелограмма. Они
пересекаются и точкой О делятся пополам.
4) Аналогично доказывается что А1А3’ и A2A4’, A1A3’ и A3A1’ пересекаются и точкой пересечения делятся пополам.
5) Отсюда, все четыре диагонали пересекаются в одной точке и делятся пополам.
Ч.Т.Д.
Чтобы вернуться, нажмите кнопку
Слайд 13В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх
его измерений
Дано: ABCDA’B’C’D’ – прямоугольный параллелепипед, AC’ - диагональ
Доказать:
АС’2 = CC’ 2 +AB’ 2 +BC 2 Доказательство:
1) Рассмотрим треуг. AC’C - прямоуг. По теореме Пифагора :
АС’2 = CC’ 2 +AС 2
2) Рассмотрим треуг. АСВ – прямоуг. По
т.Пифагора : АС2 = АВ 2 +BC 2,
3) отсюда
АС’2 = CC’ 2 +AB’ 2 +BC 2
4) Рёбра АВ, ВС, СС’ не параллельны, а следовательно, их длины являются линейными размерами параллелепипеда.
Ч.Т.Д.
Чтобы вернуться, нажмите кнопку
Теги