Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Перестановки. Сочетания. Комбинации"
Содержание
- 1. "Перестановки. Сочетания. Комбинации"
- 2. ПЕРЕСТАНОВКИОпределение 1 Перестановкой из n элементов называется
- 3. ЧИСЛО ПЕРЕСТАНОВОК№2Теорема 1. Число всех различных
- 4. ЧИСЛО ПЕРЕСТАНОВОКДоказательство теоремы 1.Любую перестановку из
- 5. ПЕРЕСТАНОВКИ С ПОВТОРЕНИЯМИТеорема 2 Число перестановок n
- 6. ЗАДАЧИ НА ПЕРЕСТАНОВКИЗадача: Сколько слов можно составить,
- 7. РАЗМЕЩЕНИЯОпределение 1 Размещением из n
- 8. ЧИСЛО РАЗМЕЩЕНИЙТеорема 1 Число всех размещений из
- 9. ЧИСЛО РАЗМЕЩЕНИЙЗамечание. Формулу для числа размещений можно записать в видеДействительно№8
- 10. ЧИСЛО РАЗМЕЩЕНИЙАбонент забыл последние 3 цифры номера
- 11. РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИОпределение 2Размещением с повторением из
- 12. ЧИСЛО РАЗМЕЩЕНИЙ С ПОВТОРЕНИЯМИТеорема 2. Число k-
- 13. ЗАДАЧИ НА РАЗМЕЩЕНИЯСколько существует номеров машин?Решение. Считаем,
- 14. ЗАДАЧИ1)Сколькими способами можно составить список из 8
- 15. ЗАДАЧИ2)Сколькими способами можно составить список 8 учеников,
- 16. ЗАДАЧИ3) Сколькими способами можно разделить 11 спортсменов
- 17. ЗАДАЧИ4) Сколькими способами можно вызвать по очереди
- 18. ЗАДАЧИ5)Сколько существует четырехзначных чисел, у которых все
- 19. ЗАДАЧИ6)Сколько существует двоичных чисел, длина которых не
- 20. ЗАДАЧИ7)В лифт 9 этажного дома зашли 7
- 21. ЗАДАЧИ8)Сколько чисел, меньше 10000 можно написать с
- 22. СОЧЕТАНИЯ№21
- 23. СОЧЕТАНИЯ№22
- 24. СОЧЕТАНИЯ. ЗАДАЧИ№23Ответ: 220 способов
- 25. СОЧЕТАНИЯ. ЗАДАЧИ№24В классе учатся 14 мальчиков и
- 26. Шаблоны для оформления презентаций по математике http://www.uchportal.ru/load/160-1-0-319261.ГИА-2013.
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Подготовка к ГИА
Комбинаторные задачи
Подготовила: учитель математики
Шахтерской ОШ І-ІІІ ступеней №
2
Слайд 2 ПЕРЕСТАНОВКИ
Определение 1
Перестановкой из n элементов называется всякий способ нумерации
этих элементов
Пример 1
Дано множество
. Составить все перестановки этого множества.Решение.
Пример 1
Дано множество . Составить все перестановки этого множества.
Решение.
№1
Слайд 3 ЧИСЛО ПЕРЕСТАНОВОК
№2
Теорема 1. Число всех различных перестановок из n
элементов равно n!
Замечание.
Считают, что 0!=1
читается «n факториал» и
вычисляется по формулеСлайд 4 ЧИСЛО ПЕРЕСТАНОВОК
Доказательство теоремы 1.
Любую перестановку из n элементов можно
получить с помощью n действий:
выбор первого элемента n различными способами,
выбор
второго элемента из оставшихся (n-1) элементов, т.е. (n-1) способом,выбор третьего элемента (n-2) способами,
……
n) выбор n-го элемента 1 способом.
По правилу умножения число всех способов выполнения действий, т.е. число перестановок, равно
№ 3
Слайд 5 ПЕРЕСТАНОВКИ С ПОВТОРЕНИЯМИ
Теорема 2
Число перестановок n – элементов, в
котором есть одинаковые элементы, а именно элементов
i –того типа ( ) вычисляется по формулегде
Доказательство.
Так как перестановки между одинаковыми элементами не изменяют вид перестановки в целом, количество перестановок всех элементов множества нужно разделить на число перестановок одинаковых элементов.
№4
Слайд 6ЗАДАЧИ НА ПЕРЕСТАНОВКИ
Задача: Сколько слов можно составить, переставив буквы в
слове «экзамен», а в слове «математика»?
Решение: В слове «экзамен» все
буквы различны, поэтому используем формулу для числа перестановок без повторенийВ слове «математика» 3 буквы «а», 2 буквы «м», 2 буквы «т», поэтому число перестановок всех букв разделим на число перестановок повторяющихся букв:
№5
Слайд 7 РАЗМЕЩЕНИЯ
Определение 1
Размещением из n элементов по k
называется всякая перестановка из k элементов, выбранных каким-либо способом из
данных n.Пример
Дано множество . Составим все 2-размещения этого множества.
№6
Слайд 8ЧИСЛО РАЗМЕЩЕНИЙ
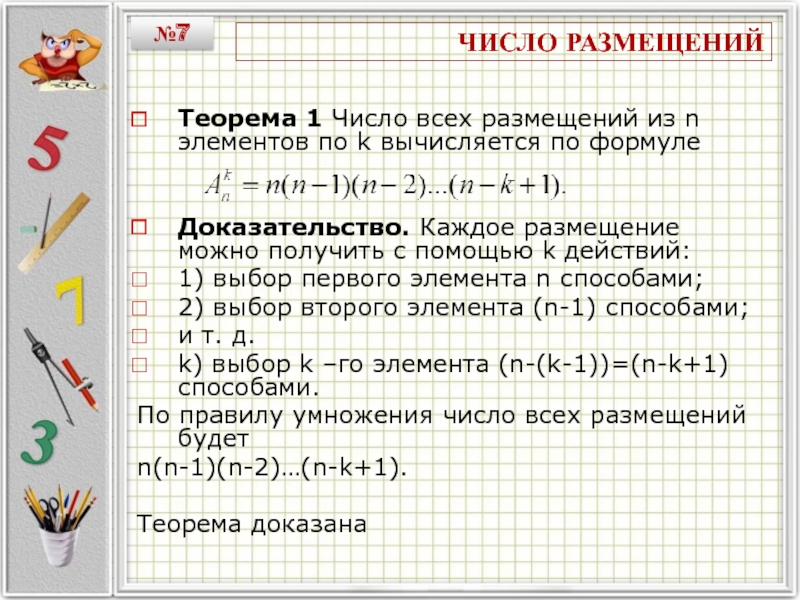
Теорема 1 Число всех размещений из n элементов по
k вычисляется по формуле
Доказательство. Каждое размещение можно получить с помощью
k действий:1) выбор первого элемента n способами;
2) выбор второго элемента (n-1) способами;
и т. д.
k) выбор k –го элемента (n-(k-1))=(n-k+1) способами.
По правилу умножения число всех размещений будет
n(n-1)(n-2)…(n-k+1).
Теорема доказана
№7
Слайд 10ЧИСЛО РАЗМЕЩЕНИЙ
Абонент забыл последние 3 цифры номера телефона. Какое максимальное
число номеров ему нужно перебрать, если он вспомнил, что эти
последние цифры разные?Задача сводится к поиску различных перестановок 3 элементов из 10 ( так как всего цифр 10). Применим формулу для числа перестановок.
№9
Решение.
Ответ: 720 номеров
Слайд 11РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ
Определение 2
Размещением с повторением из n элементов по
k называется всякая перестановка из k элементов, выбранных каким-либо способом
из данных n элементов возможно с повторениями№10
Пример
Дано множество
Составим 2- размещения с повторениями:
Слайд 12ЧИСЛО РАЗМЕЩЕНИЙ С ПОВТОРЕНИЯМИ
Теорема 2. Число k- размещений с повторениями
из
n элементов вычисляется по формуле
№11
Доказательство. Каждый элемент размещения
можно выбрать n способами. По правилу умножения число всех размещений с повторениями равно Слайд 13ЗАДАЧИ НА РАЗМЕЩЕНИЯ
Сколько существует номеров машин?
Решение. Считаем, что в трех
буквах номера машины не используются буквы «й», «ы», «ь», «ъ»,
тогда число перестановок букв равноЧисло перестановок цифр равно
По правилу умножения получим число номеров машин
Ответ: 24389000 номеров
№12
Слайд 14ЗАДАЧИ
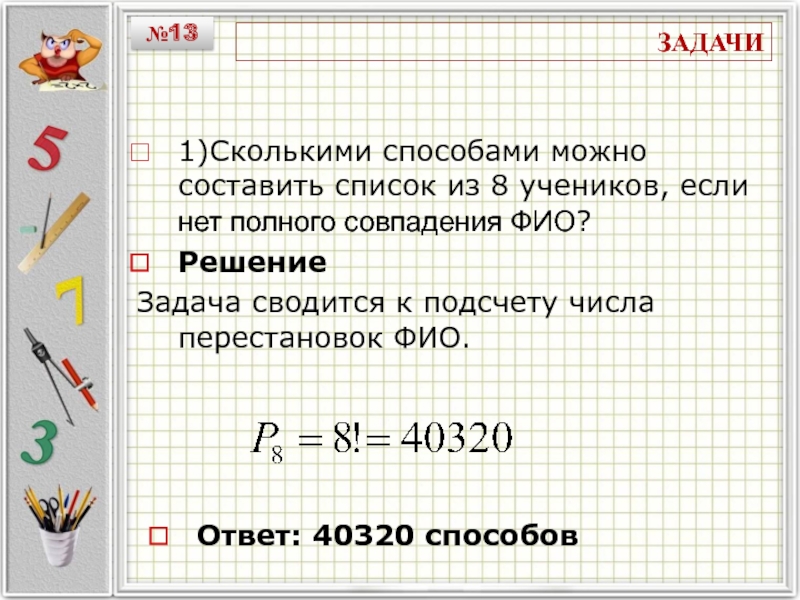
1)Сколькими способами можно составить список из 8 учеников, если нет
полного совпадения ФИО?
Решение
Задача сводится к подсчету числа перестановок ФИО.
№13
Ответ:
40320 способовСлайд 15ЗАДАЧИ
2)Сколькими способами можно составить список 8 учеников, так, чтобы два
указанных ученика располагались рядом?
Решение
Можно считать двоих указанных учеников за один
объект и считать число перестановок уже 7 объектов, т.е. Так как этих двоих можно переставлять местами друг с другом, необходимо умножить результат на 2!
№14
Ответ: 10080 способов
Слайд 16ЗАДАЧИ
3) Сколькими способами можно разделить 11 спортсменов на 3 группы
по 4, 5 и 2 человека соответственно?
Решение. Сделаем карточки: четыре
карточки с номером 1, пять карточек с номером 2 и две карточки с номером 3. Будем раздавать эти карточки с номерами групп спортсменам, и каждый способ раздачи будет соответствовать разбиению спортсменов на группы. Таким образом нам необходимо посчитать число перестановок 11 карточек, среди которых четыре карточки с одинаковым номером 1, пять карточек с номером 2 и две карточки с номером 3.Ответ: 6930 способов
№15
Слайд 17ЗАДАЧИ
4) Сколькими способами можно вызвать по очереди к доске 4
учеников из 7?
Решение. Задача сводится к подсчету числа размещений из
7 элементов по 4Ответ: 840 способов
№16
Слайд 18ЗАДАЧИ
5)Сколько существует четырехзначных чисел, у которых все цифры различны?
Решение. В
разряде единиц тысяч не может быть нуля, т.е. возможны 9
вариантов цифры.В остальных трех разрядах не может быть цифры, стоящей в разряде единиц тысяч (так как все цифры должны быть различны), поэтому число вариантов вычислим по формуле размещений без повторений из 9 по 3
Ответ: 4536 чисел
№17
По правилу умножения получим
Слайд 19ЗАДАЧИ
6)Сколько существует двоичных чисел, длина которых не превосходит 10?
Решение. Задача
сводится к подсчету числа размещений с повторениями из двух элементов
по 10Ответ: 1024 чисел
№18
Слайд 20ЗАДАЧИ
7)В лифт 9 этажного дома зашли 7 человек. Сколькими способами
они могут распределиться по этажам дома?
Решение. Очевидно, что на первом
этаже никому не надо выходить. Каждый из 7 человек может выбрать любой из 8 этажей, поэтому по правилу умножения получим Ответ: 2097152 способов
№19
Можно так же применить формулу для числа размещений с повторениями из 8 (этажей) по 7(на каждого человека по одному этажу)
Слайд 21ЗАДАЧИ
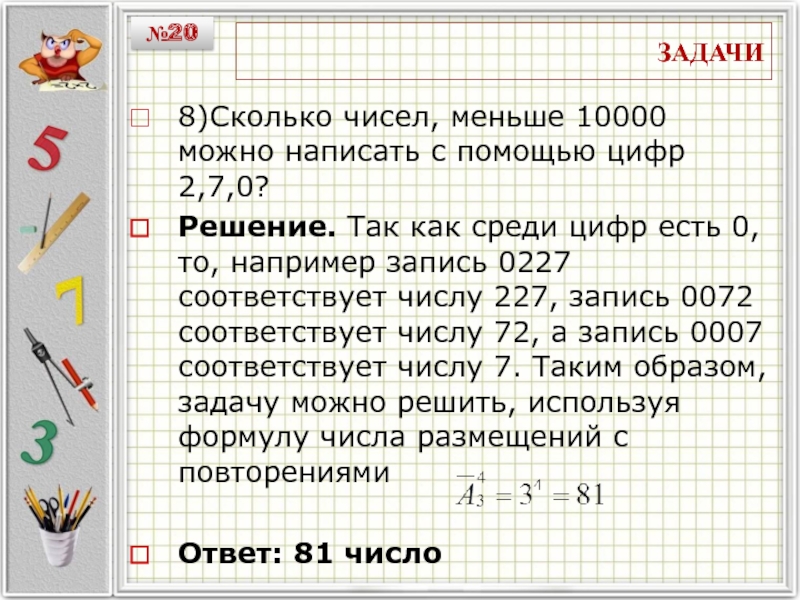
8)Сколько чисел, меньше 10000 можно написать с помощью цифр 2,7,0?
Решение.
Так как среди цифр есть 0, то, например запись 0227
соответствует числу 227, запись 0072 соответствует числу 72, а запись 0007 соответствует числу 7. Таким образом, задачу можно решить, используя формулу числа размещений с повторениямиОтвет: 81 число
№20
Слайд 25СОЧЕТАНИЯ. ЗАДАЧИ
№24
В классе учатся 14 мальчиков и 12 девочек. Для
участия в соревнованиях следует выделить четырёх мальчиков и трёх девочек.
Сколькими способами можно сделать выбор?Ответ: 220220 способов
220220
Слайд 26Шаблоны для оформления презентаций по математике
http://www.uchportal.ru/load/160-1-0-31926
1.ГИА-2013. Математика: типовые экзаменационные
варианты: 30 вариантов/ под редакцией А. Л. Семенова, И. В.
Ященко. – М.:Национальное образование, 2013.2. Математика. Базовый уровень. ГИА-2014. Пособие для «чайников»/под редакцией Ф.Ф.Лысенко, С.Ю.Калабухова.- Ростов н/Д:Легион, 2013.
3. Математика. ЕГЭ 2015. Книга 1. Базовый уровень. Профильный уровень/Д.А.Мальцев и др.- Ростов н/Д: Издатель Мальцев Д.А.; М.:Народное образование, 2015.
Список литературы
Интернет-ресурсы