Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многогранники и их построение
Содержание
- 1. Правильные многогранники и их построение
- 2. Цели и задачи:Дать понятие правильных многогранников (
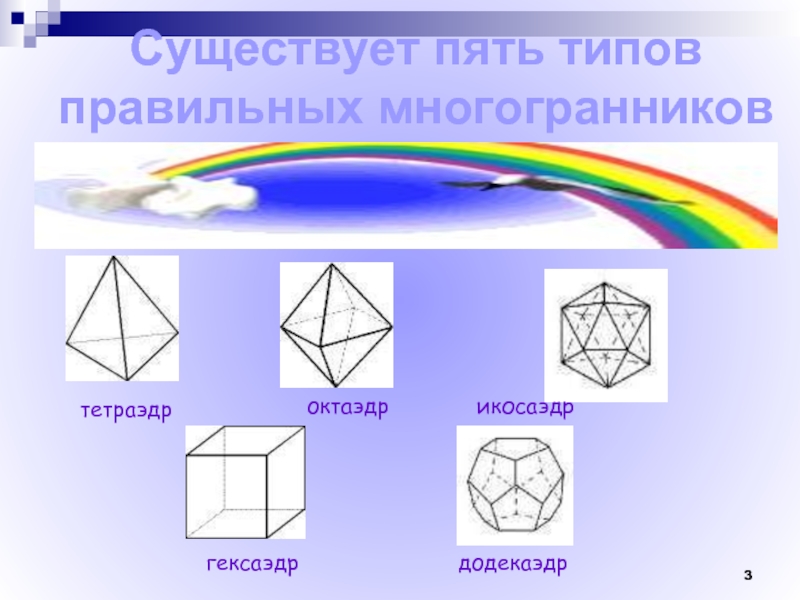
- 3. Существует пять типов правильных многогранниковтетраэдроктаэдрикосаэдргексаэдрдодекаэдр
- 4. Определение многогранника: Многогранник – это часть пространства,
- 5. Правильным называется многогранник, у которого все грани
- 6. В каждой вершине многогранника должно сходиться
- 7. Правильный многогранник, у которого грани правильные треугольники
- 8. ОКТАЭДРПравильный многогранник, у которого грани- правильные
- 9. ИКОСОЭДРПравильный многогранник, у которого грани - правильные
- 10. КУБ -правильный многогранник, у которого грани –
- 11. ДодекаэдрПравильный многогранник, у которого грани правильные пятиугольники
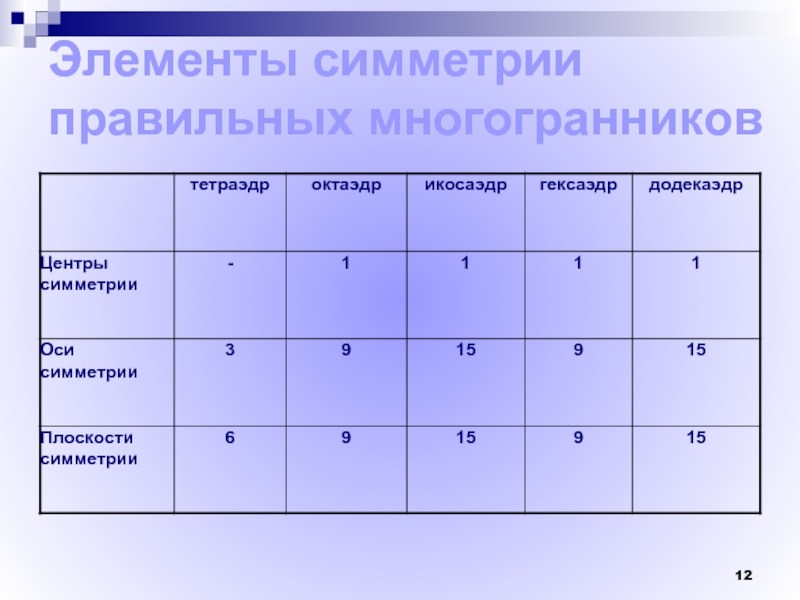
- 12. Элементы симметрии правильных многогранников
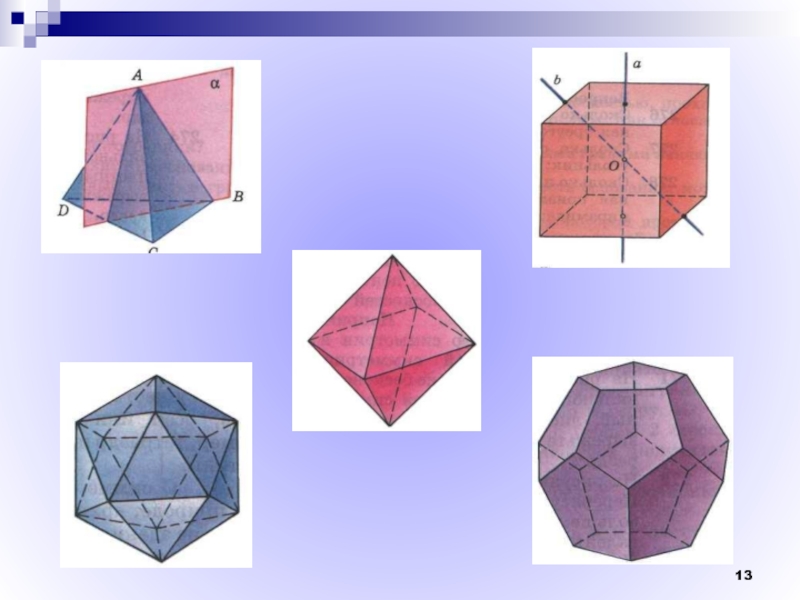
- 13. Слайд 13
- 14. Немного историиВсе типы правильных многогранников были известны
- 15. Правильные многогранники называют также «платоновыми телами» -
- 16. Олицетворение многогранников.
- 17. Дюрер. Меланхолия
- 18. Тайна мировоззрения.
- 19. Выводы:Многогранник называется правильным, если:Он выпуклый;Все его грани
- 20. Евклид ЕВКЛИД, или ЭВКЛИД - древнегреческий математик,
- 21. Платон
- 22. Определение правильного многоугольникаМногоугольник называется правильным, если у него все стороны и все углы равны.
- 23. Построение с помощью куба
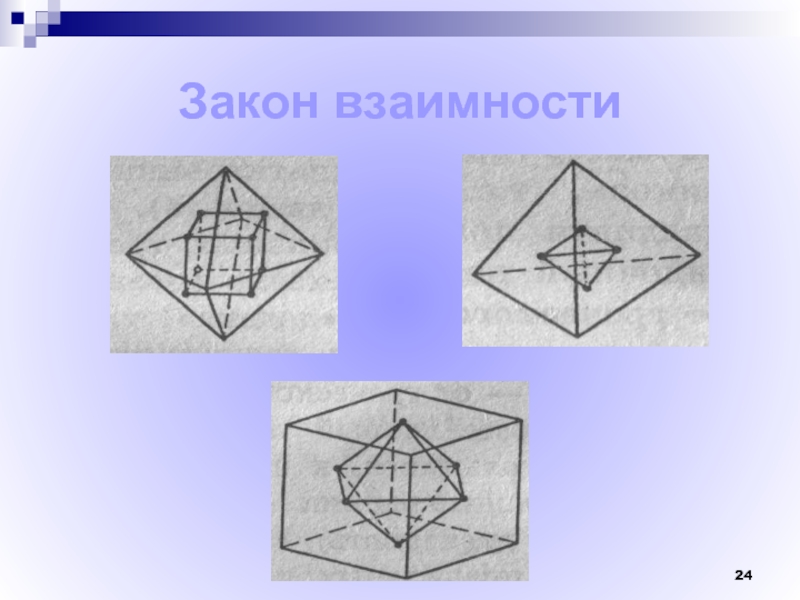
- 24. Закон взаимности
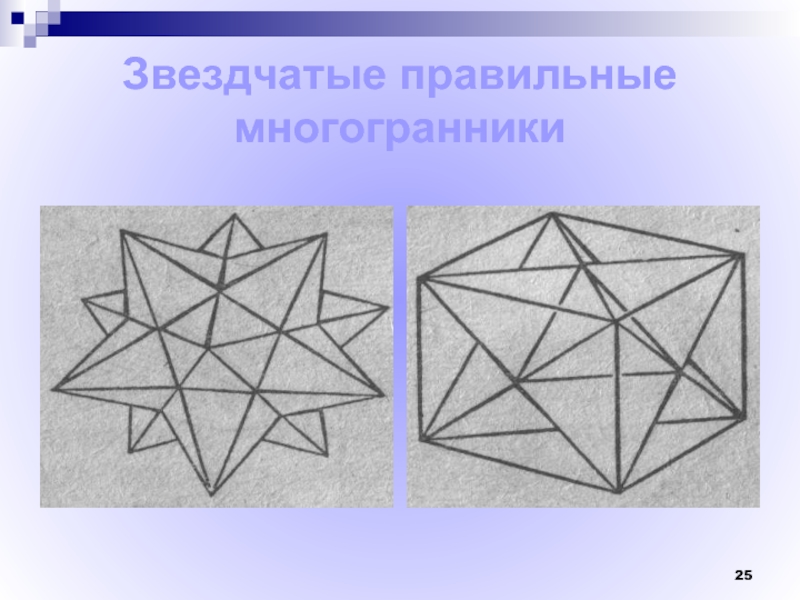
- 25. Звездчатые правильные многогранники
- 26. С1В1АПостроение правильного тетраэдра вписанного в кубРассмотрим вершину
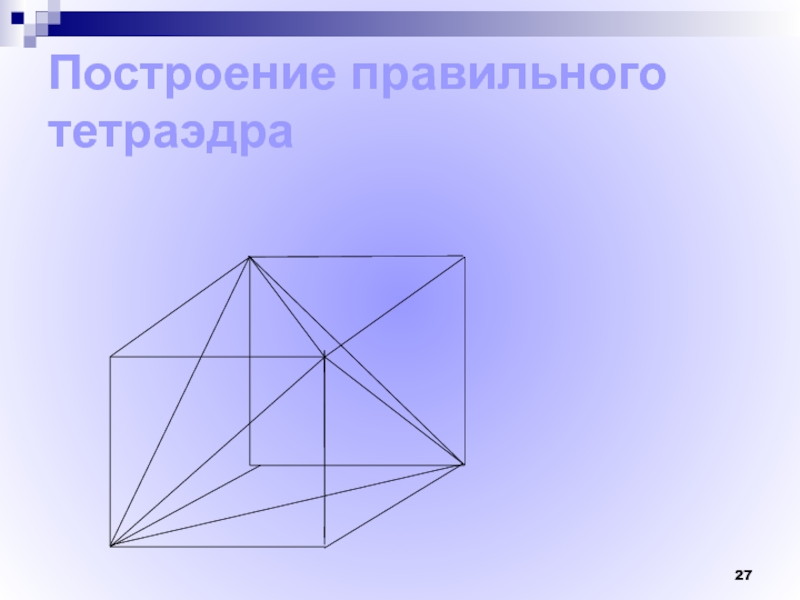
- 27. Построение правильного тетраэдра
- 28. Построение правильного октаэдра, вписанного в данный кубВыбираем
- 29. Описать около данного куба правильный октаэдрЧерез центры
- 30. Построение икосаэдра, вписанного в кубПоместим на средних
- 31. Построение додекаэдра, описанного около кубаНа каждой грани
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Правильные многогранники
и их построение.
Работу выполнила:
ученица 11 класса
МОУ «Карсинская СОШ»
Слайд 2Цели и задачи:
Дать понятие правильных многогранников ( на основе определения
многогранников).
Доказать почему существует только 5 типов правильных многогранников.
Рассмотреть свойства правильных
многогранников. Познакомить с историческими фактами, связанными с теорией правильных многогранников.
Показать, как можно с помощью куба построить другие виды правильных многогранников.
Слайд 4Определение многогранника:
Многогранник – это часть пространства, ограниченная совокупностью конечного
числа плоских многоугольников, соединённых таким образом, что каждая сторона любого
многогранника является стороной ровно одного многоугольника. Многоугольники называются гранями, их стороны – рёбрами, а вершины – вершинами.
Слайд 5Правильным называется многогранник, у которого все грани являются правильными многоугольниками,
и все многогранные углы при вершинах равны.
Приведён пример правильного
многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.
Слайд 6 В каждой вершине многогранника должно сходиться столько правильных n
– угольников, чтобы сумма их углов была меньше 3600.
Т.е должна выполняться формула βk < 3600 ( β-градусная мера угла многоугольника, являющегося гранью многогранника, k – число многоугольников, сходящихся в одной вершине многогранника.)
Слайд 7
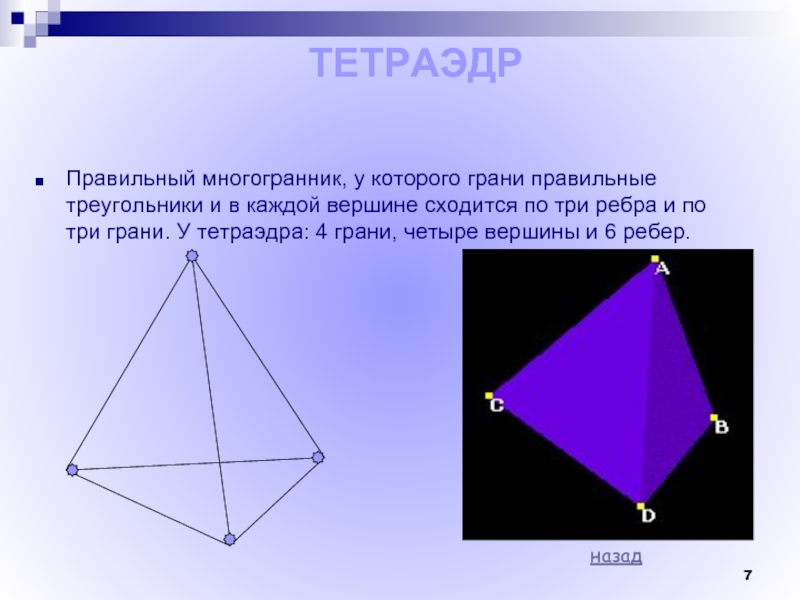
Правильный многогранник, у которого грани правильные треугольники и в каждой
вершине сходится по три ребра и по три грани. У
тетраэдра: 4 грани, четыре вершины и 6 ребер.
назад
ТЕТРАЭДР
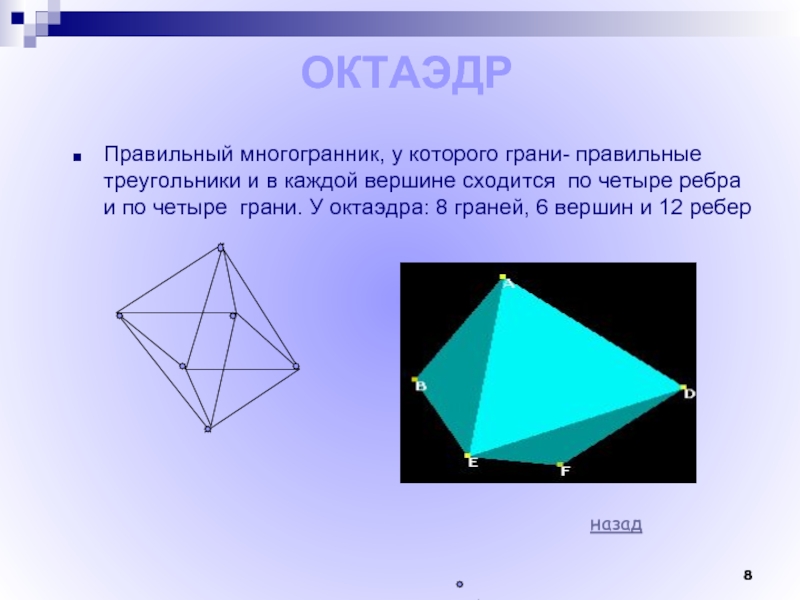
Слайд 8 ОКТАЭДР
Правильный многогранник, у которого грани- правильные треугольники и в
каждой вершине сходится по четыре ребра и по четыре грани.
У октаэдра: 8 граней, 6 вершин и 12 ребер
назад
Слайд 9ИКОСОЭДР
Правильный многогранник, у которого грани - правильные треугольники и в
вершине сходится по пять рёбер и граней. У икосаэдра:20 граней,
12 вершин и 30 реберназад
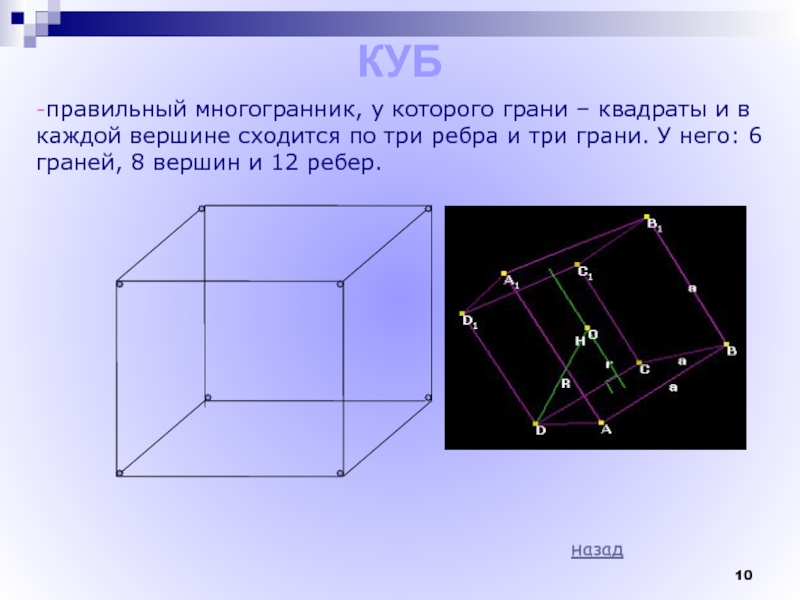
Слайд 10КУБ
-правильный многогранник, у которого грани – квадраты и в
каждой вершине сходится по три ребра и три грани. У
него: 6 граней, 8 вершин и 12 ребер.назад
Слайд 11Додекаэдр
Правильный многогранник, у которого грани правильные пятиугольники и в каждой
вершине сходится по три ребра и три грани. У додекаэдра:12
граней, 20 вершин и 30 ребер.назад
Слайд 14Немного истории
Все типы правильных многогранников были известны в Древней Греции
– именно им посвящена завершающая, XIII книга «Начал» Евклида.
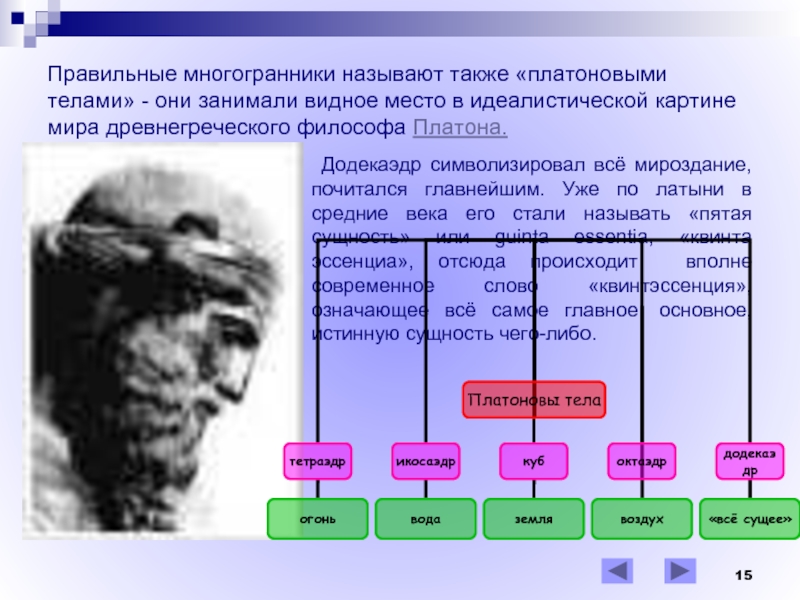
Слайд 15Правильные многогранники называют также «платоновыми телами» - они занимали видное
место в идеалистической картине мира древнегреческого философа Платона.
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.
Слайд 19Выводы:
Многогранник называется правильным, если:
Он выпуклый;
Все его грани равные правильные многоугольники;
В
каждой вершине сходится одно число граней;
Все его двугранные углы равны.
Слайд 20Евклид
ЕВКЛИД, или ЭВКЛИД - древнегреческий математик, автор первых дошедших
до нас теоретических трактатов по математике. Годы жизни - около
365 - 300 до н.э.О жизни Евклида почти ничего не известно. Некоторые биографические данные сохранились на страницах арабской рукописи XII века: "Евклид, сын Наукрата, известный под именем "Геометра", ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира".
Он родился в АфинахОн родился в Афинах, учился в Академии. В начале 3 века до н.э. переехал в Александрию и там основал математическую школу и написал для ее учеников свой фундаментальный труд, объединенный под общим названием "НАЧАЛА". Он был написан около 325 года до нашей эры.
Слайд 21 Платон
Платон (Platon)
(род. 427 - ум. 347 гг.до н.э.) - греческий философ.
Родился в Афинах. Настоящее имя Платона было Аристокл. Прозвище Платон (Широкоплечий) было ему дано в молодости за мощное телосложение. Происходил из знатного рода и получил прекрасное образование. Возможно, слушал лекции гераклитика Кратила, знал популярные в Афинах сочинения Анаксагора, был слушателем Протагора и других софистов. В 407 г. стал учеником Сократа, что определило всю его жизнь и творчество. Согласно легенде, после первого же разговора с ним Платон сжег свою трагическую тетралогию, подготовленную для ближайших Дионисий. Целых восемь лет он не отходил от любимого учителя, образ которого он с таким пиететом рисовал впоследствии в своих диалогах. В 399 г. Сократ, приговоренный к смерти, закончил жизнь в афинском узилище. Платон, присутствовавший на процессе, не был с Сократом в его последние минуты. Возможно, опасаясь за собственную жизнь, он покинул Афины и с несколькими друзьями уехал в Мегару. Оттуда он поехал в Египет и Кирену (где встретился с Аристиппом и математиком Феодором), а затем в Южную Италию — колыбель элеатизма (Парменид, Зенон Элейский) и пифагорейства (Пифагор).
Слайд 22Определение правильного многоугольника
Многоугольник называется правильным, если у него все стороны
и все углы равны.
Слайд 26С1
В1
А
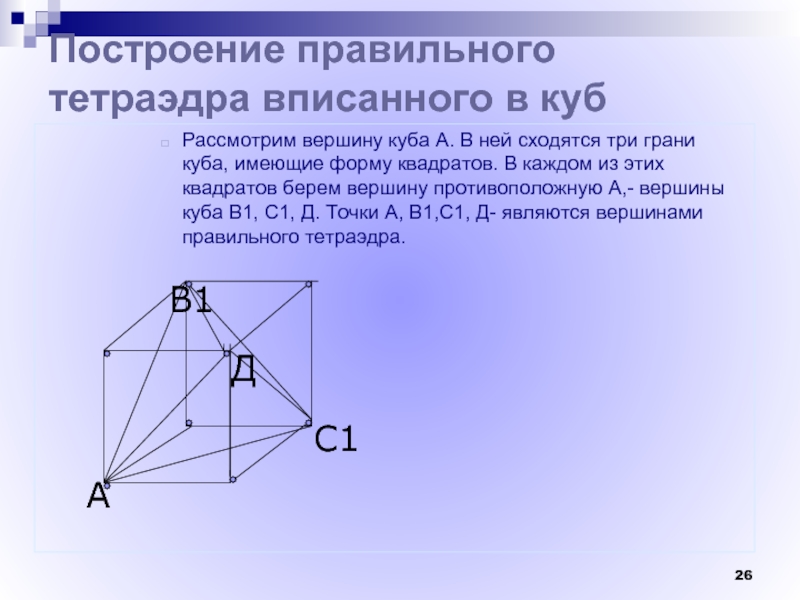
Построение правильного тетраэдра вписанного в куб
Рассмотрим вершину куба А. В
ней сходятся три грани куба, имеющие форму квадратов. В каждом
из этих квадратов берем вершину противоположную А,- вершины куба В1, С1, Д. Точки А, В1,С1, Д- являются вершинами правильного тетраэдра.Д
Слайд 28Построение правильного октаэдра, вписанного в данный куб
Выбираем куб. В нем
последовательно проводим отрезки: слабо видимыми линиями соединяем попарно между собой
вершины каждой грани. Точки пересечения этих диагоналей соединяем между собой.Слайд 29Описать около данного куба правильный октаэдр
Через центры противоположных
граней куба
проведем прямые,
которые пересекаются в точке О- центре куба- и
являются взаимно перпендикулярными. На каждой из этих прямых по обе стороны от точки О отложим отрезки длиной 1,5 а, Где а- длина ребра куба. Концы этих отрезков являются вершинами правильного октаэдра. Далее последовательно соединяем эти вершины.
O