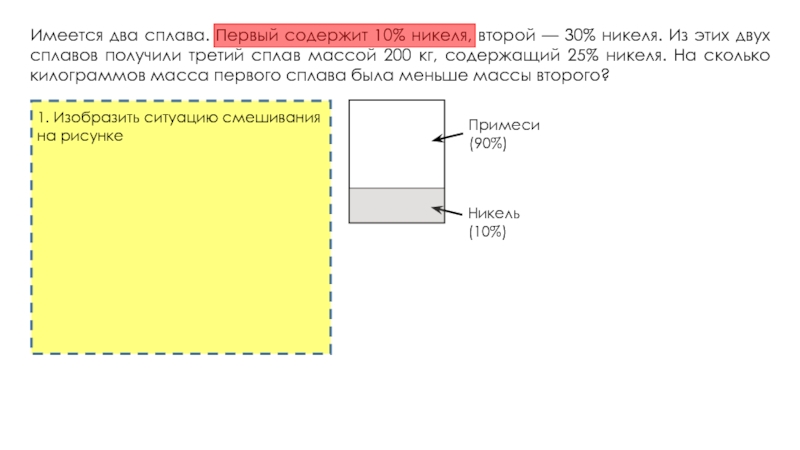
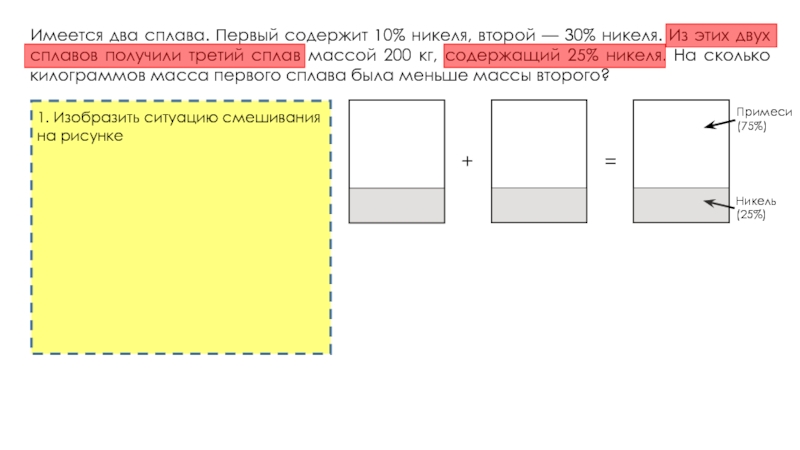
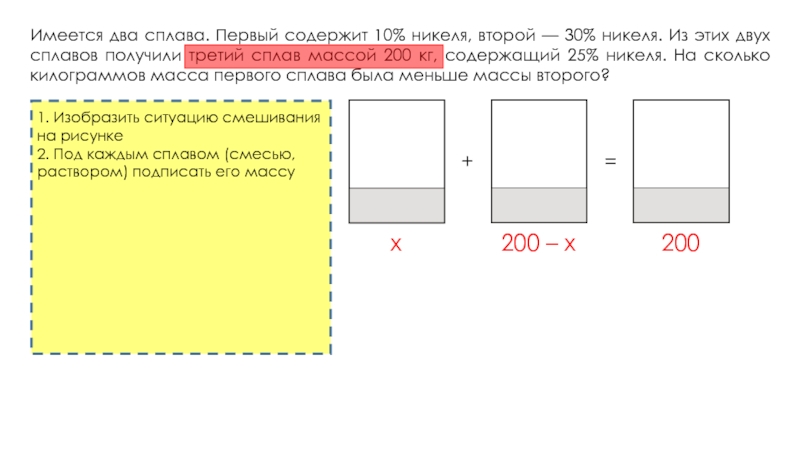
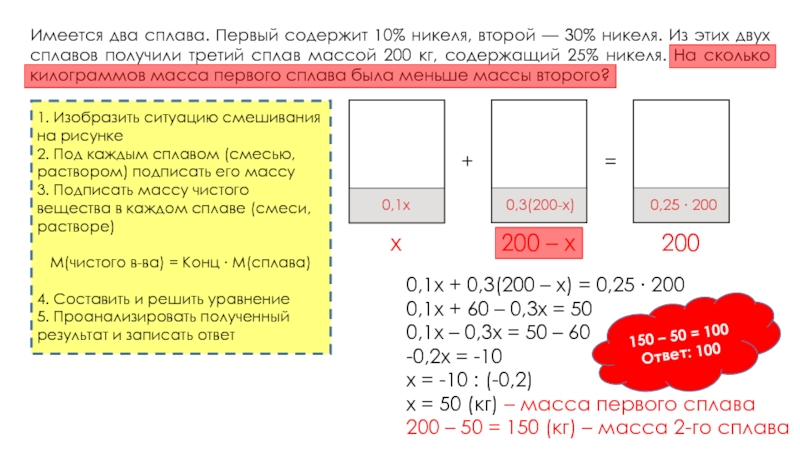
никеля. Из этих двух сплавов получили третий сплав массой 200
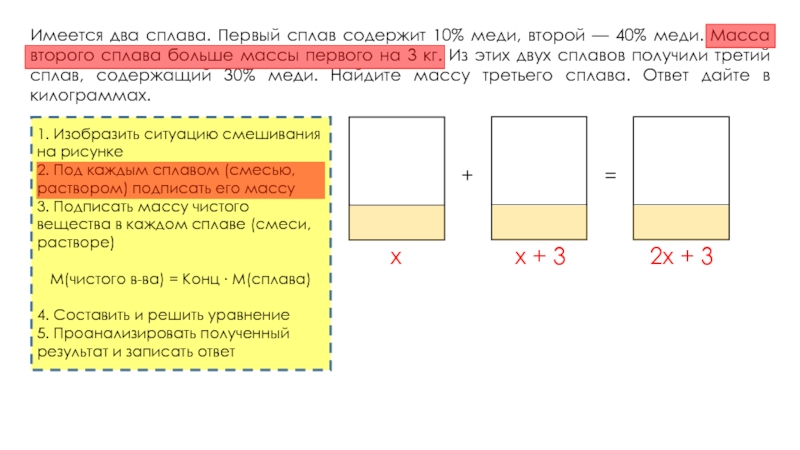
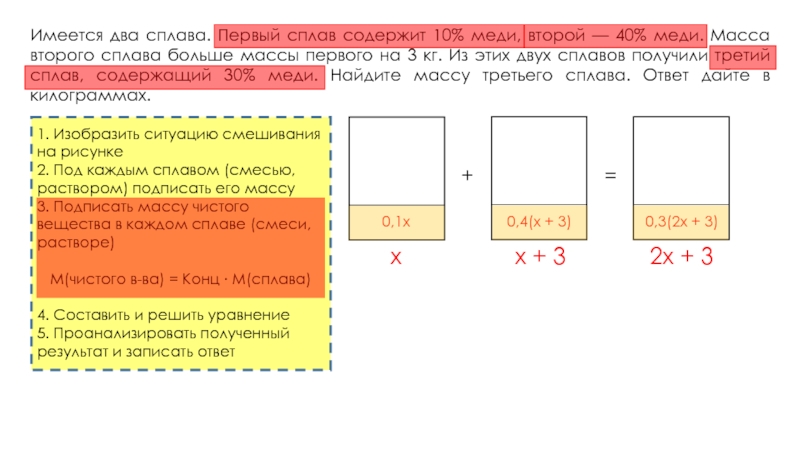
кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
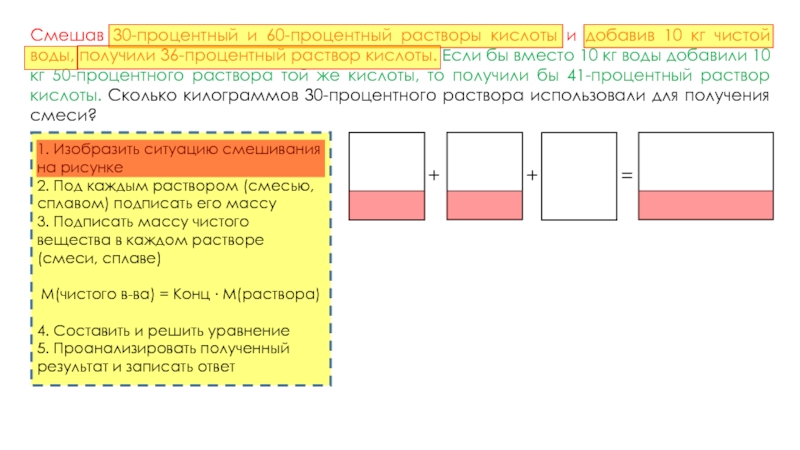
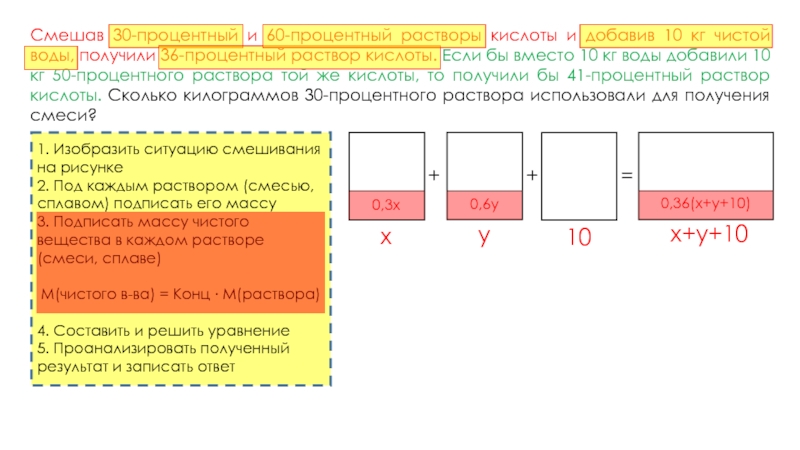
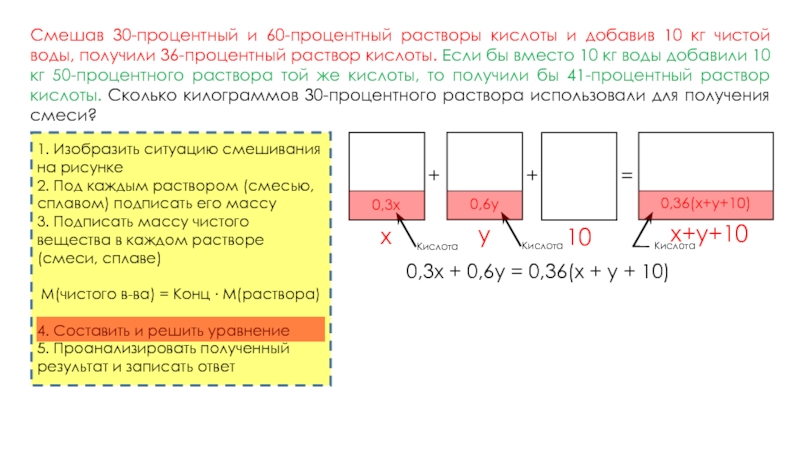
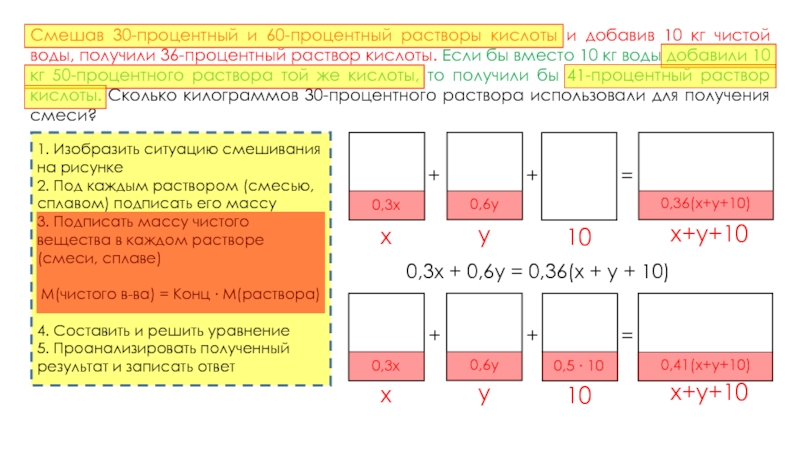
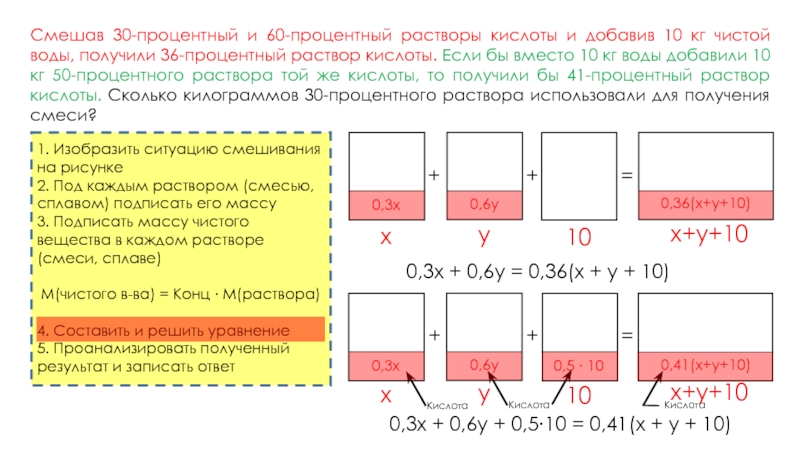
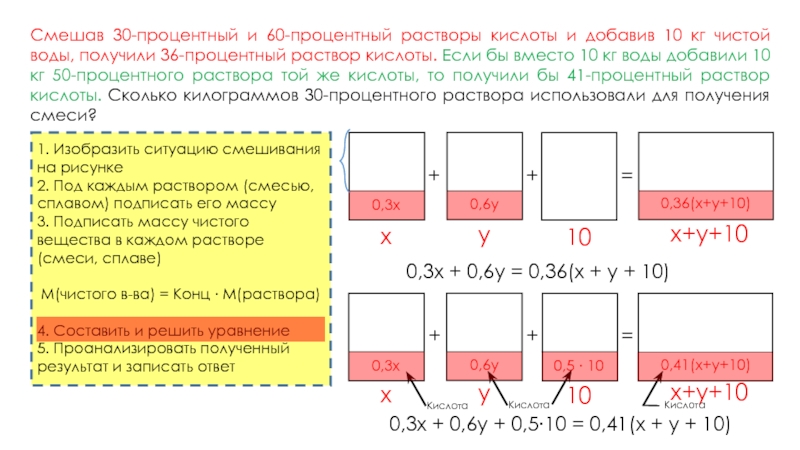
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
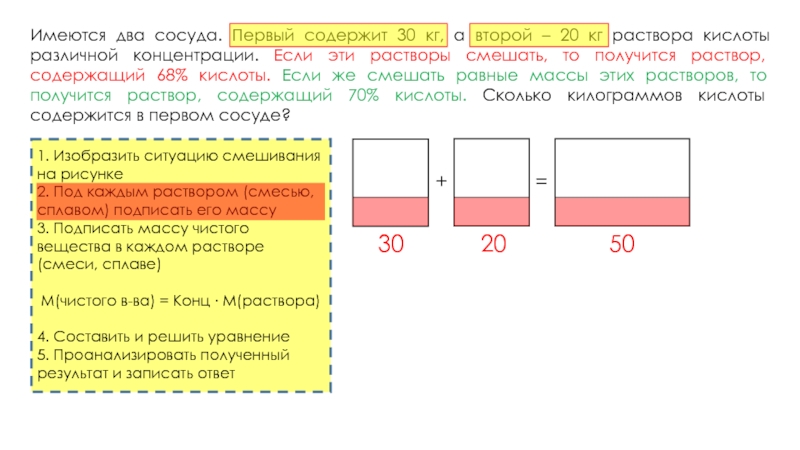
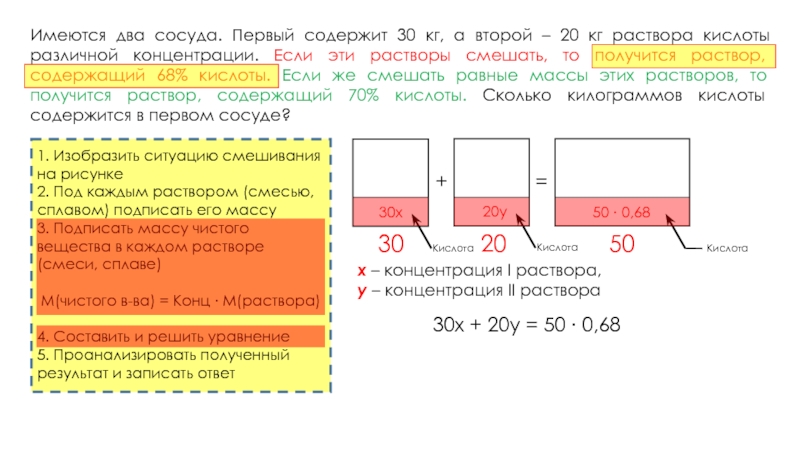
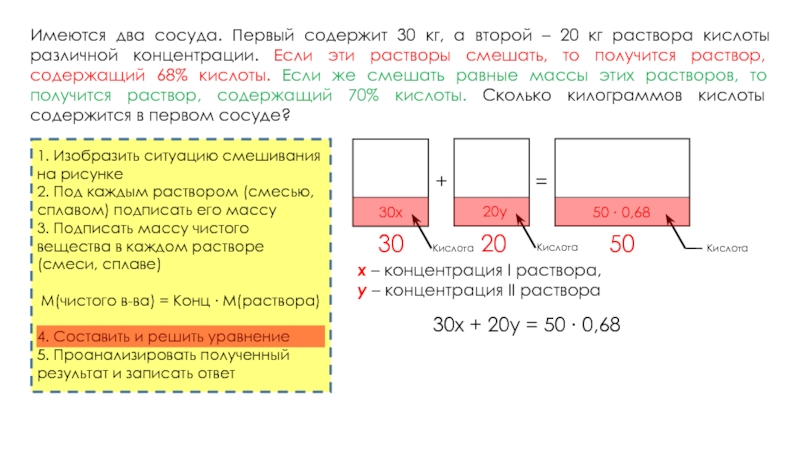
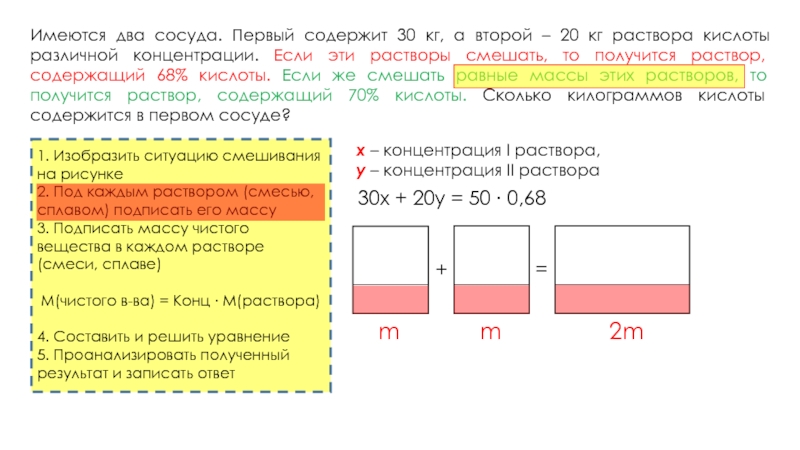
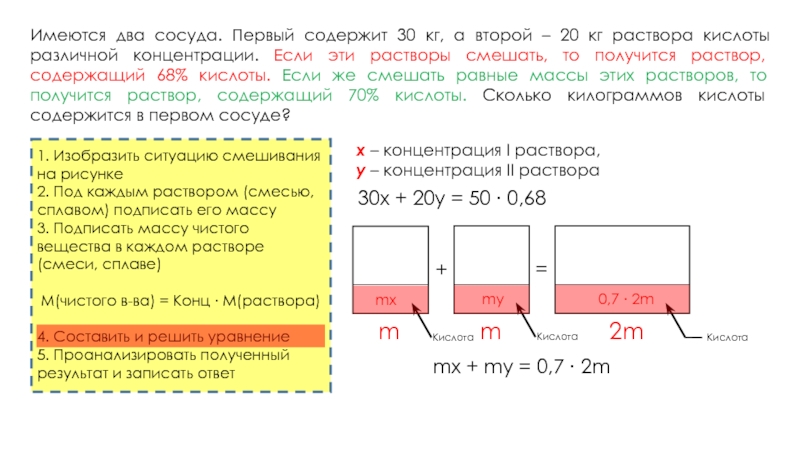
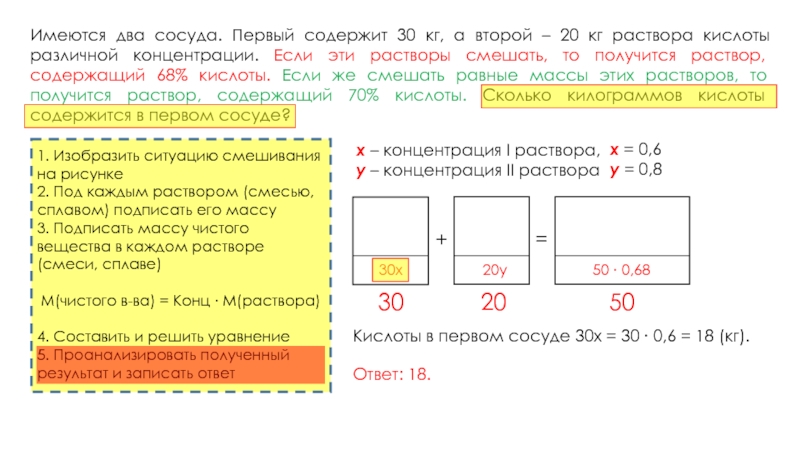
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
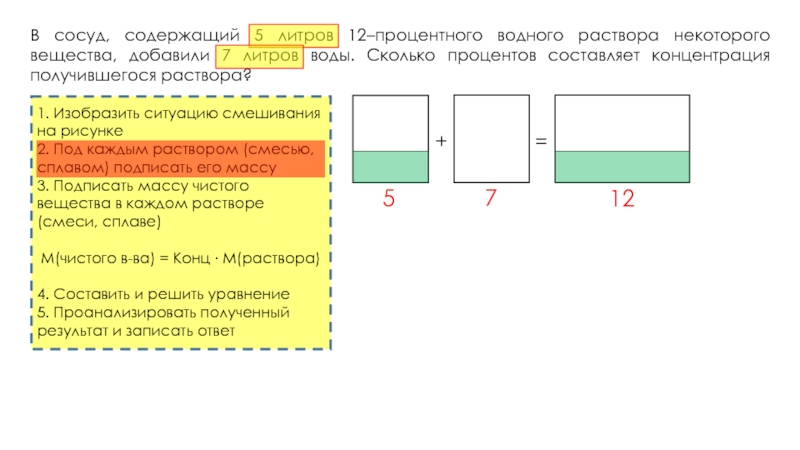
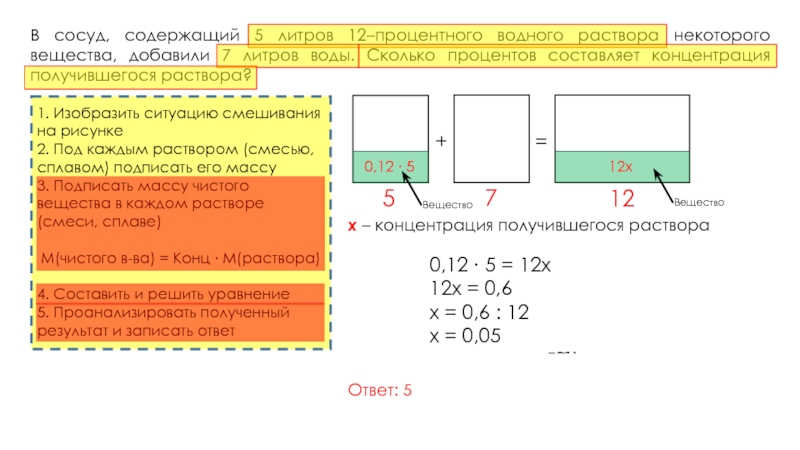
В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
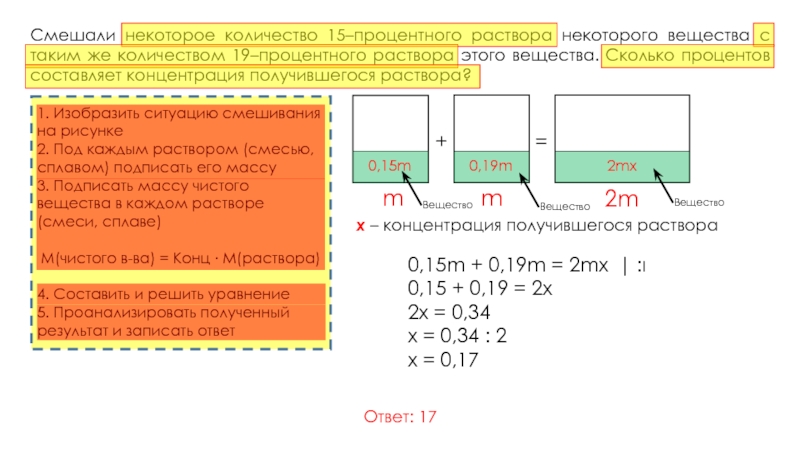
Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?