Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ломаная. Длина ломаной. Выпуклые многоугольники
Содержание
- 1. Ломаная. Длина ломаной. Выпуклые многоугольники
- 2. Цель урока: изучение учащимися нового определения и
- 3. А1А2А3А4А5А6А1А2А3А4А5А6 – Ломаная.Точки А1, А2, А3, А4,
- 4. Простая ломанаяЛоманая с самопересечениемЛоманная называется простой, если она не имеет самопересечений.
- 5. Задание: -начертите ломаную и назовите её элементы-назовите
- 6. Назовите вид изображенных ломаных
- 7. Замкнутая ломаная. Если начало и конец ломанной совпадают, то она называется замкнутой. А1А2А3А4
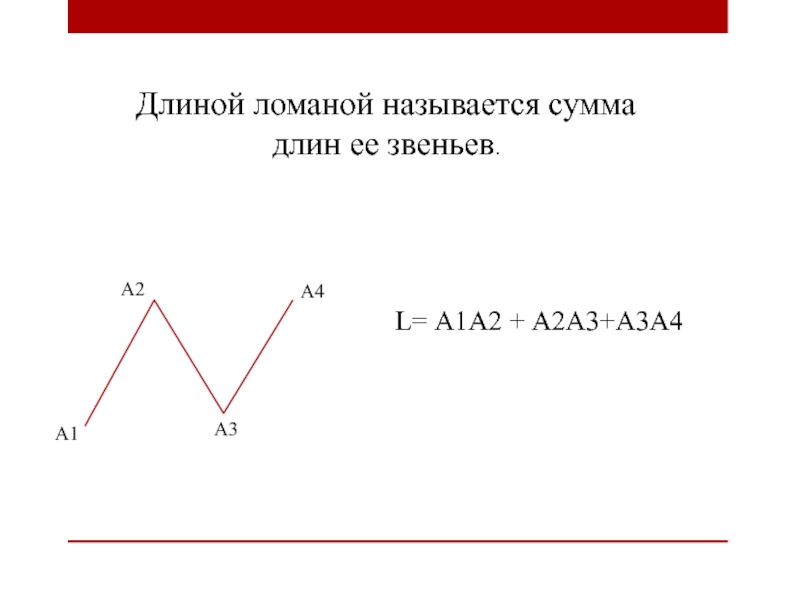
- 8. А1А2А3А4L= А1А2 + А2А3+А3А4Длиной ломаной называется сумма длин ее звеньев.
- 9. Задание: Существует ли треугольник со сторонами 5, 7 и 13см?
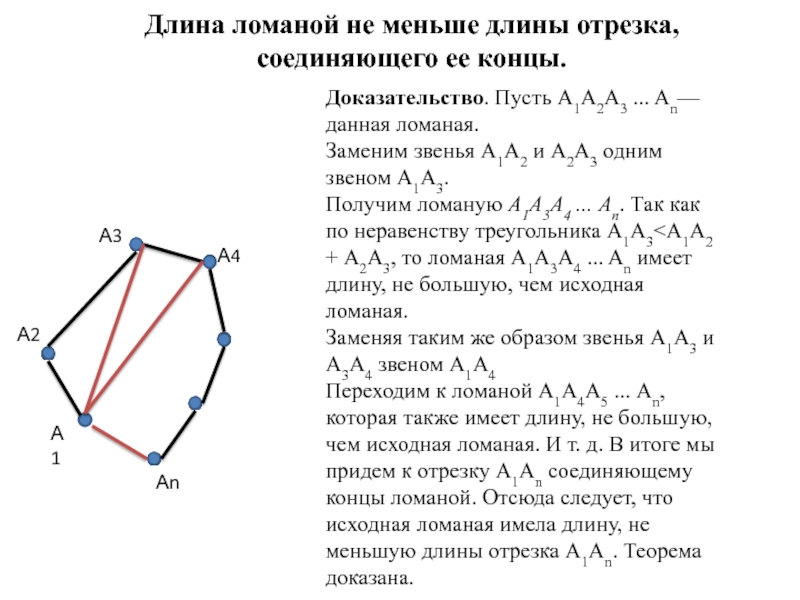
- 10. Длина ломаной не меньше длины отрезка, соединяющего
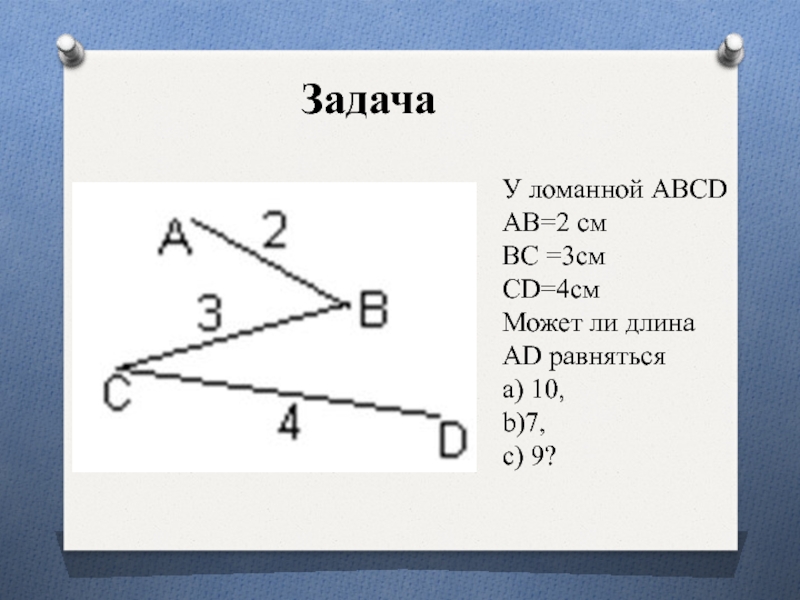
- 11. ЗадачаУ ломанной ABCD AB=2 смBC =3смCD=4см Может ли длина AD равняться а) 10, b)7, с) 9?
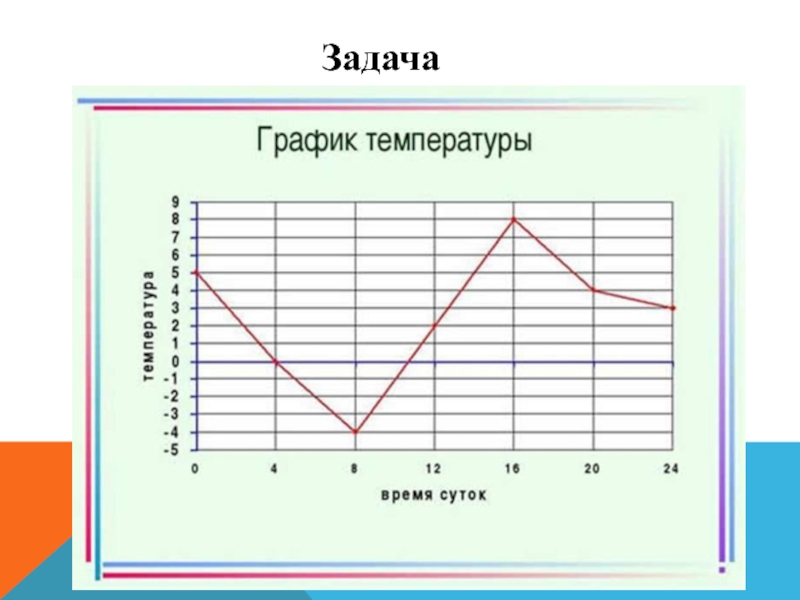
- 12. Задача
- 13. Примеры ломаных из окружающего мира
- 14. Простая замкнутая ломаная называется многоугольником, если ее
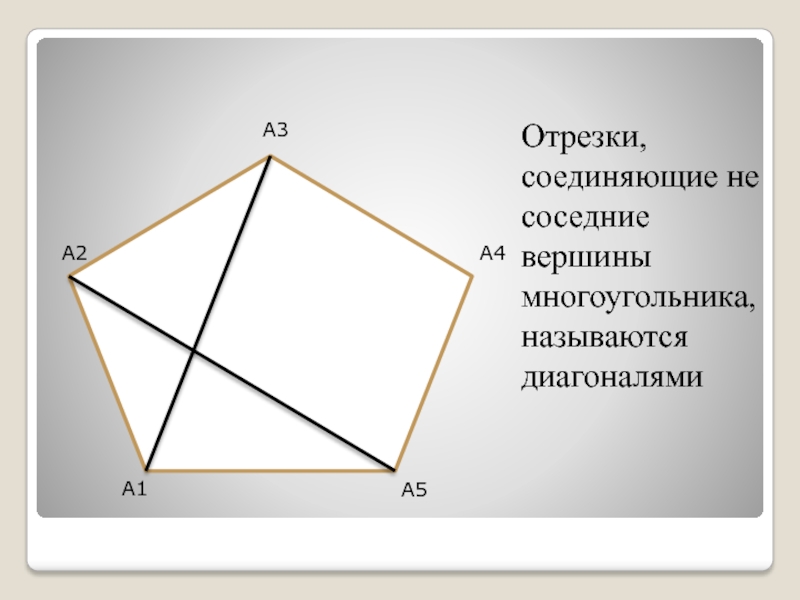
- 15. А1А2А3А4А5Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями
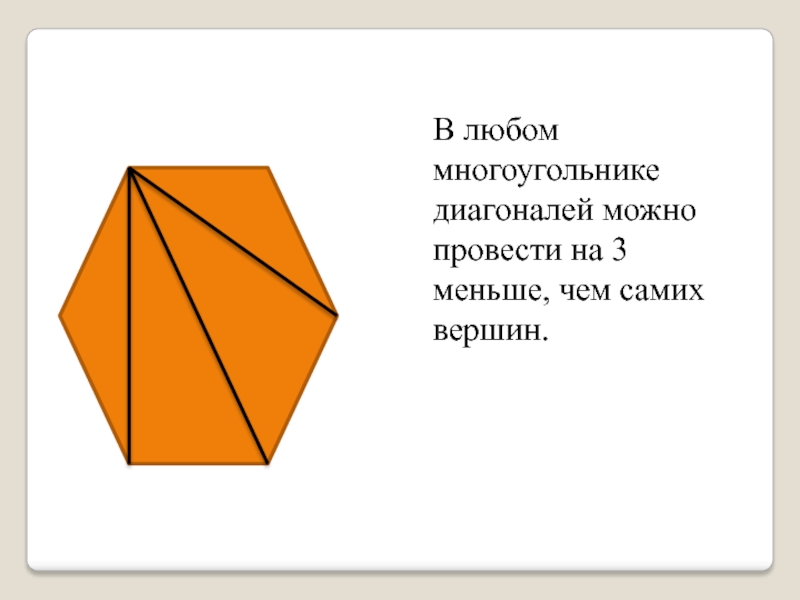
- 16. В любом многоугольнике диагоналей можно провести на 3 меньше, чем самих вершин.
- 17. Периметр многоугольникаПериметром многоугольника называется сумма всех его сторон
- 18. АBПлоским многоугольником или многоугольной областью называется конечная
- 19. Выпуклый многоугольникМногоугольник называется выпуклым, если он лежит
- 20. B1B2B3B4B5 – невыпуклый многоугольник, если он лежит
- 21. ˂ВAD – угол многоугольникаУглом многоугольника при данной
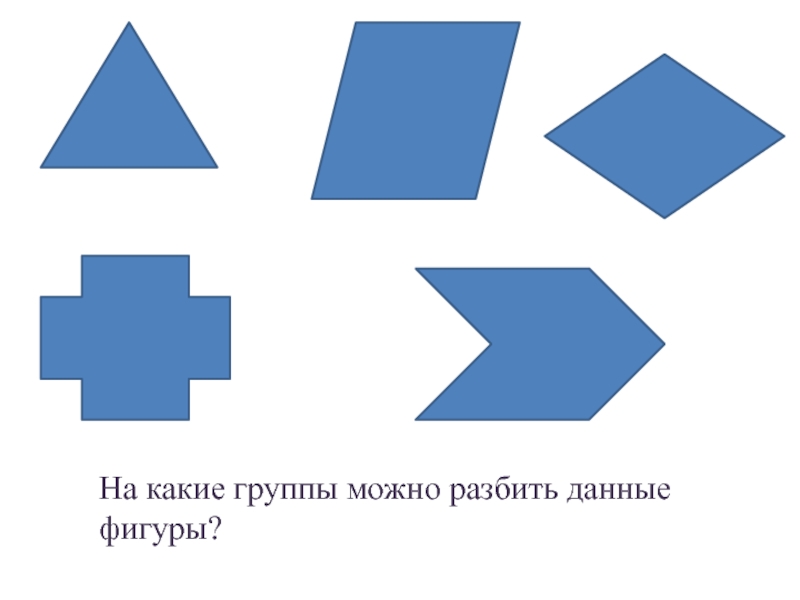
- 22. На какие группы можно разбить данные фигуры?
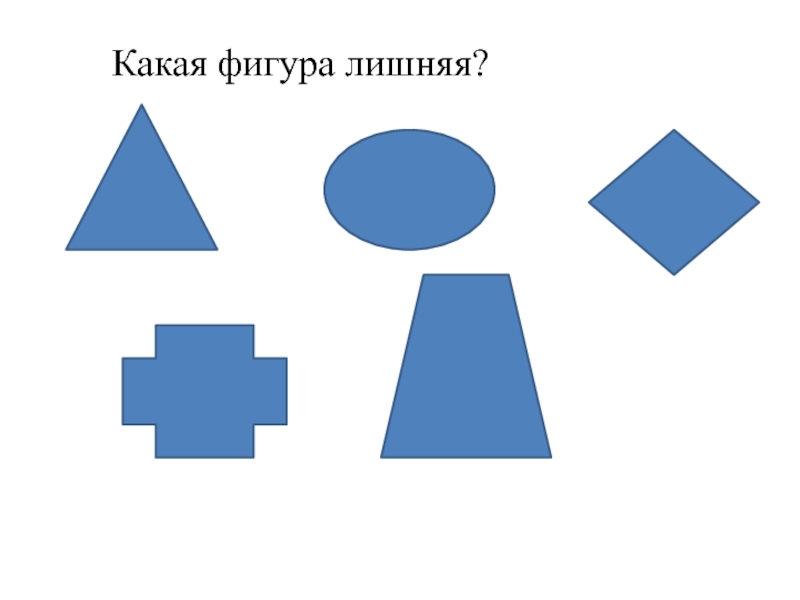
- 23. Какая фигура лишняя?
- 24. Вам предлагается работа на проверку полученных знаний 1.Выбрать
- 25. Домашнее заданиеП. 113, 114 до теоремыN 6 стр. 179
- 26. Рефлексия.Расположите себя на лестнице успеха:Я знаюЯ понимаю Я умею
- 27. Скачать презентанцию
Цель урока: изучение учащимися нового определения и понимания: ломаная, элементы ломаной длина ломаной, многоугольник, элементы многоугольника, выпуклый и невыпуклый многоугольник.
Слайды и текст этой презентации
Слайд 3А1
А2
А3
А4
А5
А6
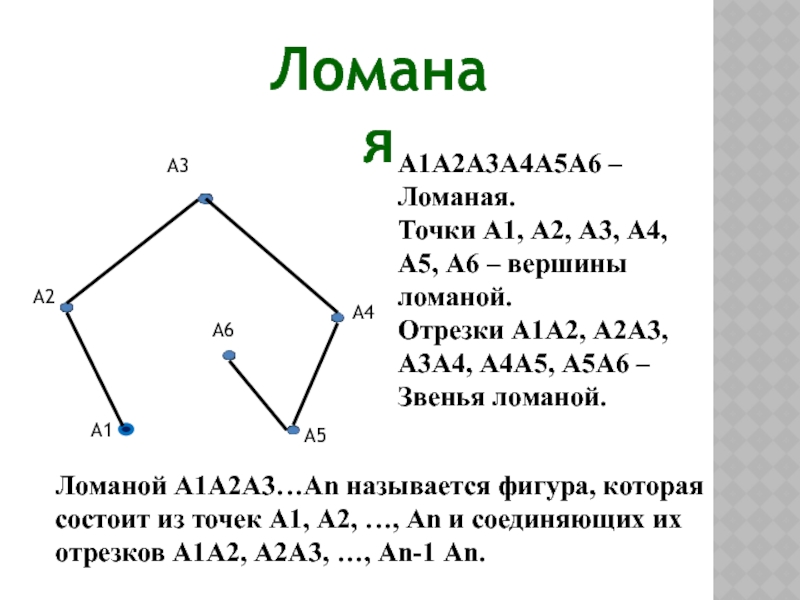
А1А2А3А4А5А6 – Ломаная.
Точки А1, А2, А3, А4, А5, А6 –
вершины ломаной.
Отрезки А1А2, А2А3, А3А4, А4А5, А5А6 – Звенья ломаной.
Ломаной
А1А2А3…Аn называется фигура, которая состоит из точек А1, А2, …, Аn и соединяющих их отрезков А1А2, А2А3, …, Аn-1 Аn.Ломаная
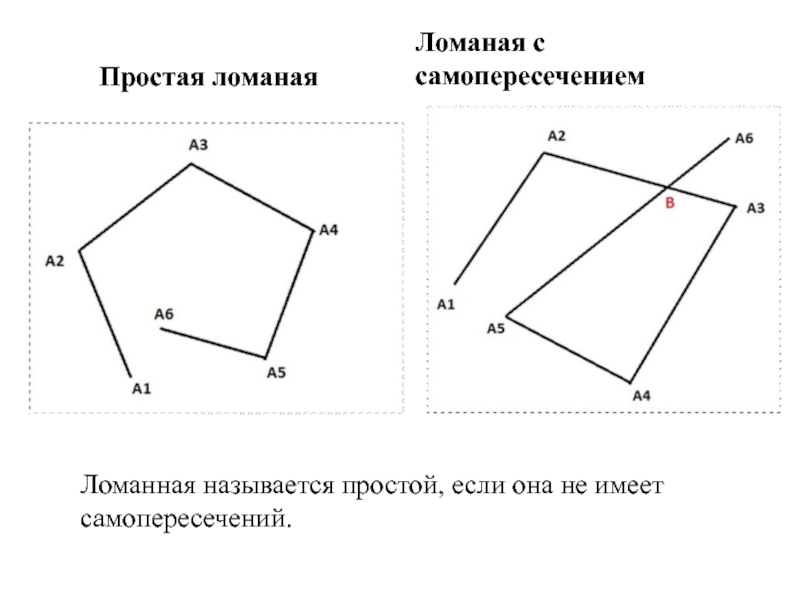
Слайд 4Простая ломаная
Ломаная с самопересечением
Ломанная называется простой, если она не имеет
самопересечений.
Слайд 5Задание:
-начертите ломаную и назовите её элементы
-назовите соседние вершины и
звенья
ломаной
записать все углы при вершинах.
назовите не соседние вершины
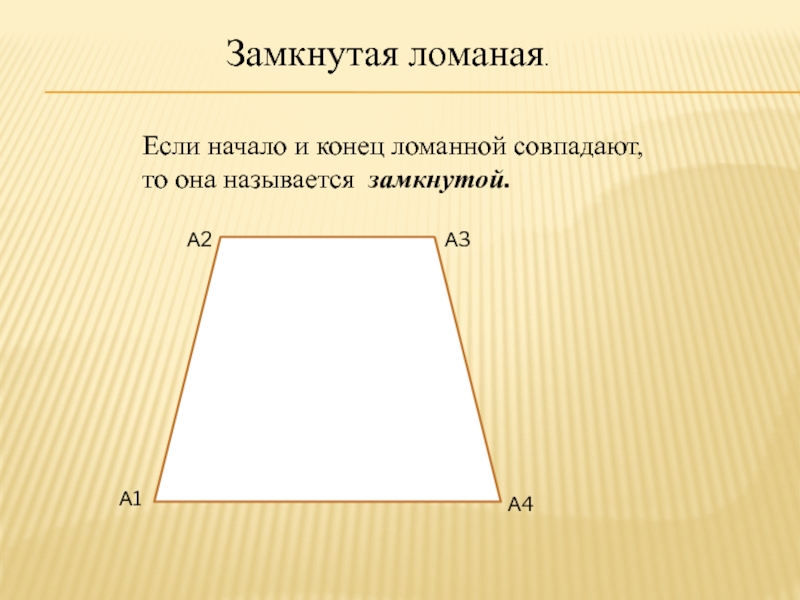
Слайд 7Замкнутая ломаная.
Если начало и конец ломанной совпадают, то она
называется замкнутой.
А1
А2
А3
А4
Слайд 10Длина ломаной не меньше длины отрезка, соединяющего ее концы.
Доказательство.
Пусть А1А2А3 ... An— данная ломаная.
Заменим звенья А1А2 и
А2А3 одним звеном А1А3. Получим ломаную А1А3А4 ... An. Так как по неравенству треугольника А1А3<А1А2 + А2А3, то ломаная A1A3A4 ... An имеет длину, не большую, чем исходная ломаная.
Заменяя таким же образом звенья А1А3 и А3А4 звеном А1А4
Переходим к ломаной А1А4А5 ... Аn, которая также имеет длину, не большую, чем исходная ломаная. И т. д. В итоге мы придем к отрезку A1An соединяющему концы ломаной. Отсюда следует, что исходная ломаная имела длину, не меньшую длины отрезка A1An. Теорема доказана.
А1
А2
А3
Аn
А4
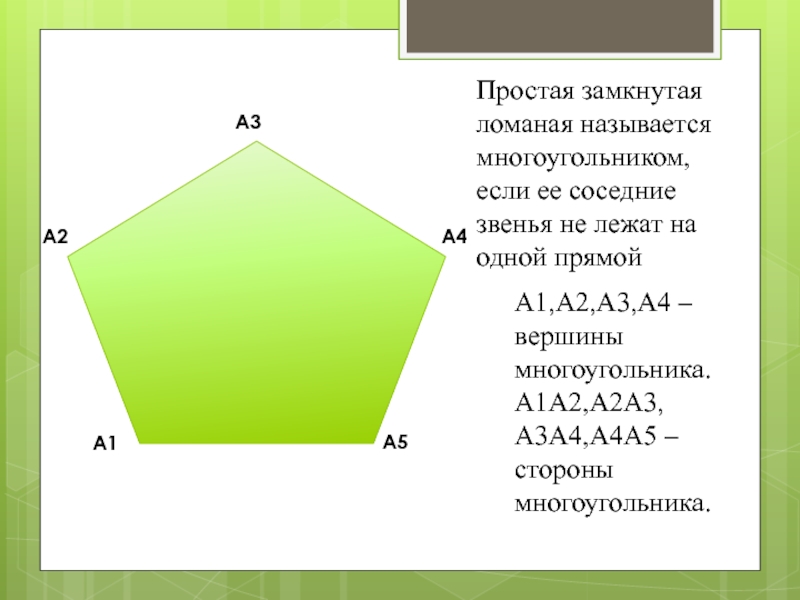
Слайд 14Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не
лежат на одной прямой
А1
А2
А3
А4
А5
А1,А2,А3,А4 – вершины многоугольника.
А1А2,А2А3,А3А4,А4А5 – стороны многоугольника.
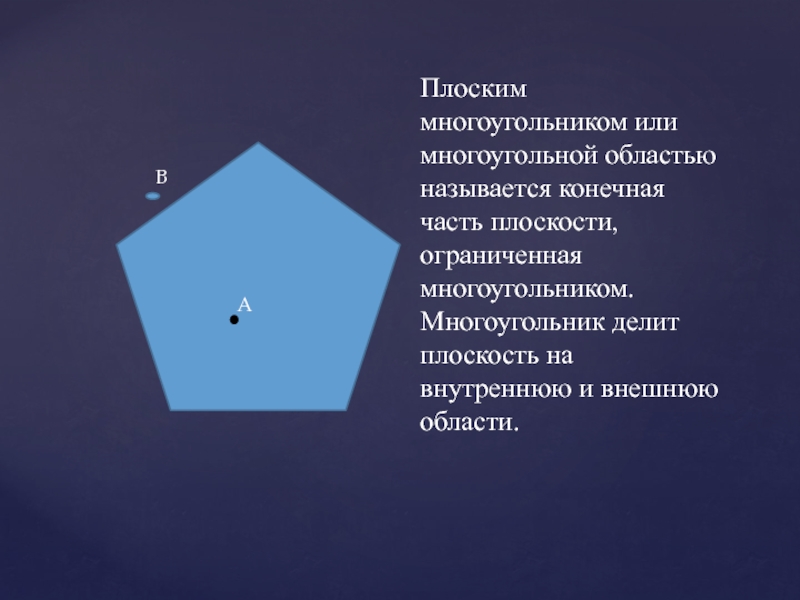
Слайд 18А
B
Плоским многоугольником или многоугольной областью называется конечная часть плоскости, ограниченная
многоугольником.
Многоугольник делит плоскость на внутреннюю и внешнюю области.
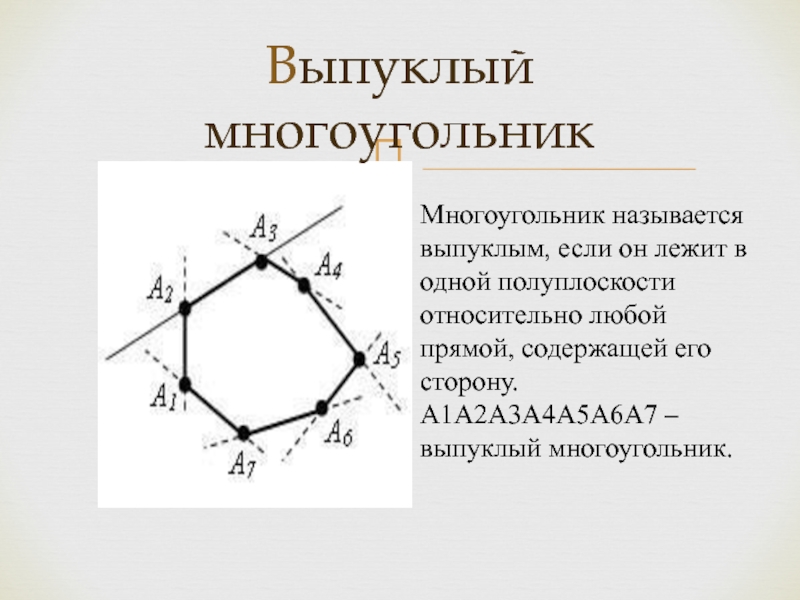
Слайд 19Выпуклый многоугольник
Многоугольник называется выпуклым, если он лежит в одной полуплоскости
относительно любой прямой, содержащей его сторону.
A1A2A3A4A5A6A7 – выпуклый многоугольник.
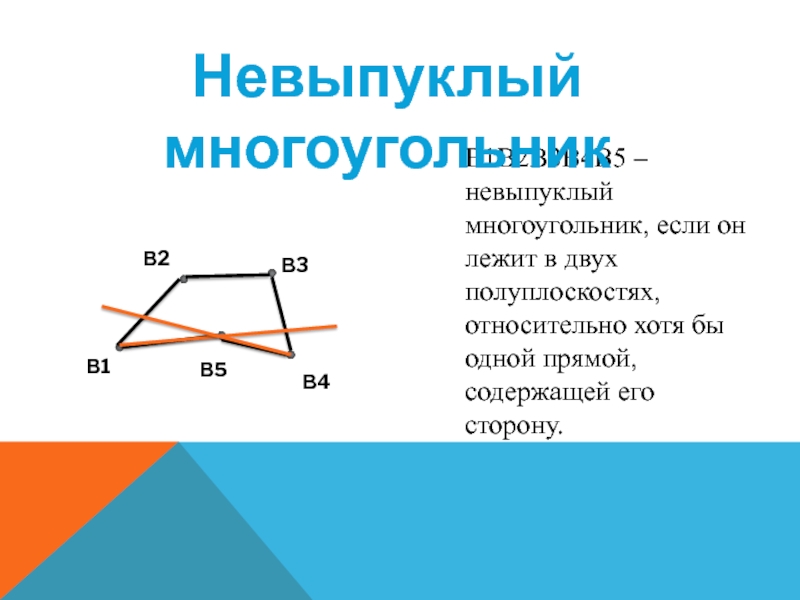
Слайд 20B1B2B3B4B5 – невыпуклый многоугольник, если он лежит в двух полуплоскостях,
относительно хотя бы одной прямой, содержащей его сторону.
Невыпуклый многоугольник
В1
В2
В3
В4
В5
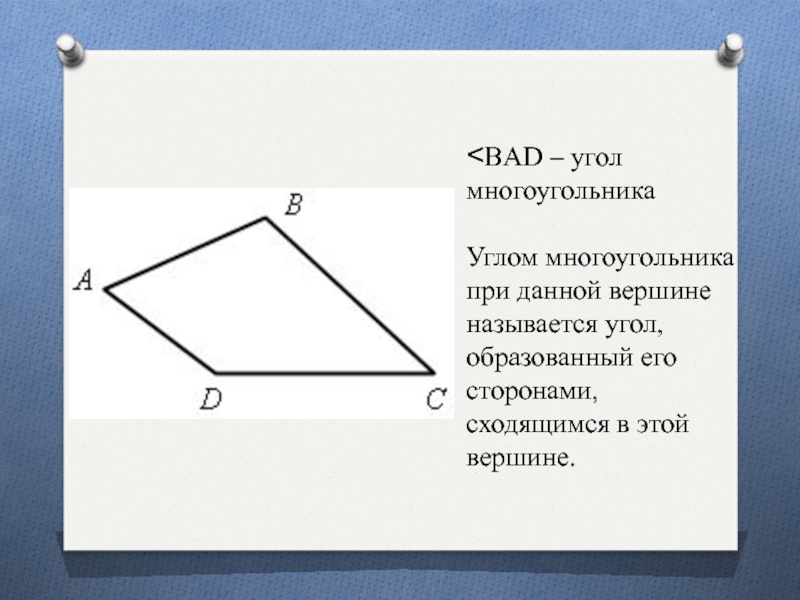
Слайд 21˂ВAD – угол многоугольника
Углом многоугольника при данной вершине называется угол,
образованный его сторонами, сходящимся в этой вершине.
Слайд 24Вам предлагается работа на проверку полученных знаний
1.Выбрать из предложенных многоугольников
те, которые не являются выпуклыми
Через каждую вершину выпуклого многоугольника проходит
четыре диагонали. Найти число сторон многоугольника.1) 7;
2) 5;
3) 6;
4) 8.