Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ВСЁ по обыкновенным дробям (6 класс)
Содержание
- 1. ВСЁ по обыкновенным дробям (6 класс)
- 2. 9.9.17СодержаниеПовторимОсновное свойство дробиСокращение дробейПриведение дробей к общему
- 3. 9.9.17ПовторимТолковый словарь «Дробь – число, состоящее из частей единицы».
- 4. 9.9.17ПовторимОбыкновенная дробь состоит из числителя, знаменателя и
- 5. 9.9.17ПовторимДроби бывают: правильными и
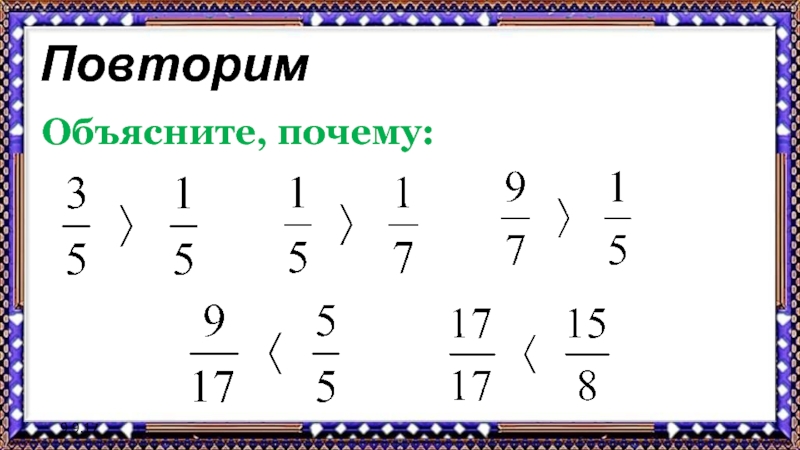
- 6. 9.9.17ПовторимОбъясните, почему:
- 7. 9.9.17 6 класс
- 8. 9.9.17Основное свойство дробиЕСЛИ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ ДРОБИ
- 9. 9.9.17Основное свойство дробиДВЕ РАВНЫЕ ДРОБИ ЯВЛЯЮТСЯ РАЗЛИЧНЫМИ ЗАПИСЯМИ ОДНОГО И ТОГО ЖЕ ЧИСЛА.
- 10. 9.9.17Задание (решаем самостоятельно)Разделите числитель и знаменатель каждой дроби на 9.
- 11. 9.9.17Работаем по учебнику
- 12. 9.9.17Сокращение дробейДЕЛЕНИЕ ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ НА ИХ
- 13. 9.9.17Сокращение дробейНАИБОЛЬШЕЕ ЧИСЛО, НА КОТОРОЕ МОЖНО СОКРАТИТЬ
- 14. 9.9.17Сокращение дробейПРИ СОКРАЩЕНИИ ДРОБЕЙ ТАК ЖЕ ИСПОЛЬЗУЮТ РАЗЛОЖЕНИЕ ЧИСЛА НА ПРОСТЫЕ МНОЖИТЕЛИ
- 15. 9.9.17ЗаданиеСократите дроби:
- 16. 9.9.17Работаем по учебнику
- 17. 9.9.17Приведение дробей к общему знаменателюЛЮБЫЕ ДВЕ ДРОБИ
- 18. 9.9.17Приведение дробей к общему знаменателюНапример: 5/6 и
- 19. 9.9.17Приведение дробей к общему знаменателюЧтобы привести дроби
- 20. 9.9.17Работаем по учебникустр. №
- 21. 9.9.17Сравнение дробейЧтобы сравнить дроби с разными знаменателями,
- 22. 9.9.17ЗаданиеСравните дробиРешение. 1) Приведём дроби к
- 23. 9.9.17ЗаданиеРасположите дроби в порядке возрастанияПлан решения: 1).
- 24. 9.9.17Задание (решаем самостоятельно)Сравните дробиОтветы:
- 25. 9.9.17Работаем по учебникустр. №
- 26. 9.9.17Сложение и вычитание дробей с разными знаменателямиЧтобы
- 27. 9.9.17Сложение и вычитание дробей с разными знаменателямиДля дробей, как и для натуральных чисел, выполняются свойства сложения:
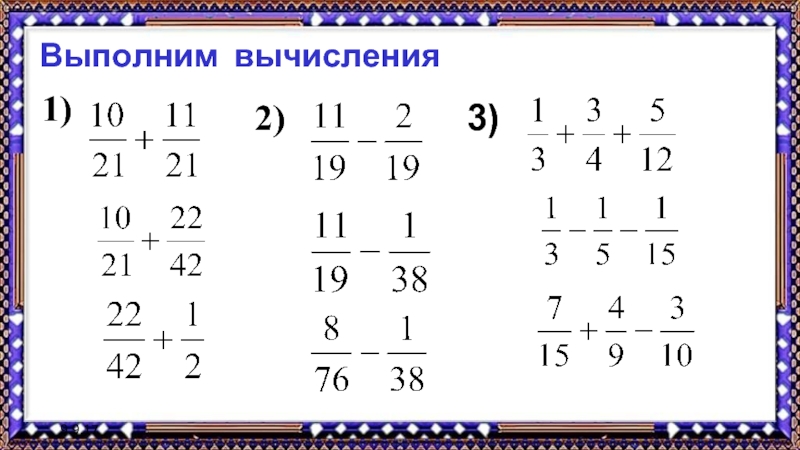
- 28. 9.9.17Выполним вычисления 1) 2) 3)
- 29. 9.9.17Сложение и вычитание смешанных чиселЧТОБЫ СЛОЖИТЬ (
- 30. 9.9.17Сложение и вычитание смешанных чиселЕСЛИ ДРОБНАЯ ЧАСТЬ
- 31. 9.9.17Работаем по учебникустр. №
- 32. 9.9.17Умножение дробей Чтобы умножить дробь на дробь,
- 33. 9.9.17Умножение дробейДля дробей, как и для натуральных
- 34. 9.9.17Обратим вниманиеПри умножении дробей не всегда надо
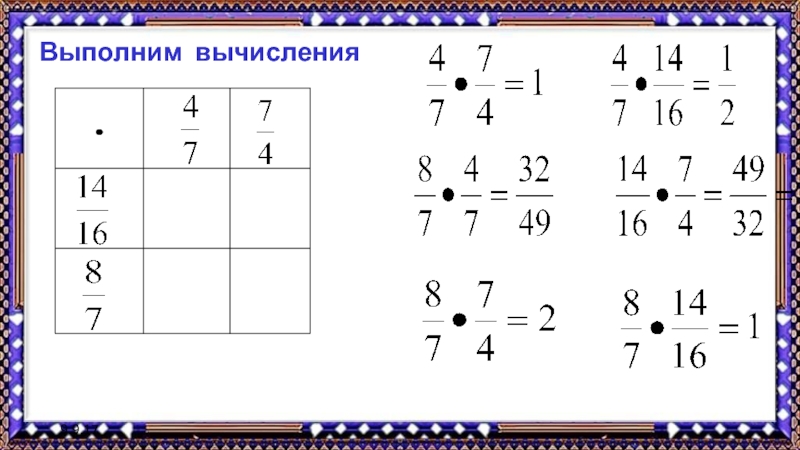
- 35. 9.9.17Выполним вычисления
- 36. 9.9.17Взаимно обратные числаДва числа (дроби), произведение которых равно 1, называются взаимно обратными.Например
- 37. 9.9.17Умножение смешанных чиселЧтобы умножить смешанные числа надо
- 38. 9.9.17Работаем по учебникустр. №
- 39. 9.9.17Деление дробейЧтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.Т.е.
- 40. 9.9.17Обратим вниманиечтоИ на нуль делить нельзя
- 41. 9.9.17Деление смешанных чиселЧтобы разделить смешанные числа надо
- 42. 9.9.17Работаем по учебникустр. №
- 43. 9.9.17Преобразование обыкновенной дроби в десятичнуюЧтобы преобразовать обыкновенную
- 44. 9.9.17Преобразование обыкновенной дроби в десятичнуюЧтобы преобразовать несократимую
- 45. 9.9.17Обратим вниманиеПри делении натурального числа на натуральное
- 46. 9.9.17Работаем по учебникустр. №
- 47. 9.9.17Удачи в изучении математики
- 48. Источники ресурсаШаблон создан на основе клипарта рамкиhttp://abload.de/img/gzdeforumdnyas-png-ce32u4u.pngИ
- 49. Скачать презентанцию
9.9.17СодержаниеПовторимОсновное свойство дробиСокращение дробейПриведение дробей к общему знаменателюСравнение дробейСложение и вычитание дробей с разными знаменателямиУмножение и деление дробейПреобразование обыкновенной дроби в десятичную
Слайды и текст этой презентации
Слайд 1ВСЁ по обыкновенным дробям
6 класс
УМК: А.Г. Мерзляк
Разработано учителем математики
МОУ
«СОШ» п. Аджером
Слайд 29.9.17
Содержание
Повторим
Основное свойство дроби
Сокращение дробей
Приведение дробей к общему знаменателю
Сравнение дробей
Сложение и
вычитание дробей с разными знаменателями
Умножение и деление дробей
Преобразование обыкновенной дроби
в десятичную
Слайд 49.9.17
Повторим
Обыкновенная дробь состоит из
числителя, знаменателя и дробной черты.
Знаменатель дроби показывает,
на
сколько равных частей разделено целое.
Числитель показывает, сколько частей взяли.
Слайд 89.9.17
Основное свойство дроби
ЕСЛИ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ ДРОБИ УМНОЖИТЬ ИЛИ РАЗДЕЛИТЬ
НА ОДНО И ТО ЖЕ НАТУРАЛЬНОЕ ЧИСЛО, ТО ПОЛУЧИТСЯ РАВНАЯ
ЕЙ ДРОБЬ.×
:
Слайд 99.9.17
Основное свойство дроби
ДВЕ РАВНЫЕ ДРОБИ ЯВЛЯЮТСЯ РАЗЛИЧНЫМИ ЗАПИСЯМИ ОДНОГО И
ТОГО ЖЕ ЧИСЛА.
Слайд 129.9.17
Сокращение дробей
ДЕЛЕНИЕ ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ НА ИХ ОБЩИЙ ДЕЛИТЕЛЬ, ОТЛИЧНЫЙ
ОТ ЕДИНИЦЫ, НАЗЫВАЮТ СОКРАЩЕНИЕМ ДРОБИ.
- несократимая дробь
Слайд 139.9.17
Сокращение дробей
НАИБОЛЬШЕЕ ЧИСЛО, НА КОТОРОЕ МОЖНО СОКРАТИТЬ ДРОБЬ, - ЭТО
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ ЕЁ ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ.
У НЕСОКРАТИМОЙ ДРОБИ ЧИСЛИТЕЛЬ
И ЗНАМЕНАТЕЛЬ – ЭТО ВЗАИМНО ПРОСТЫЕ ЧИСЛАПРИ СОКРАЩЕНИИ ДРОБЕЙ ИСПОЛЬЗУЮТ ПРИЗНАКИ ДЕЛИМОСТИ
Слайд 149.9.17
Сокращение дробей
ПРИ СОКРАЩЕНИИ ДРОБЕЙ ТАК ЖЕ ИСПОЛЬЗУЮТ РАЗЛОЖЕНИЕ ЧИСЛА НА
ПРОСТЫЕ МНОЖИТЕЛИ
Слайд 179.9.17
Приведение дробей к общему знаменателю
ЛЮБЫЕ ДВЕ ДРОБИ (или несколько дробей)
МОЖНО ПРИВЕСТИ К ОДНОМУ И ТОМУ ЖЕ ЗНАМЕНАТЕЛЮ, ИЛИ, ИНАЧЕ,
К ИХ ОБЩЕМУ ЗНАМЕНАТЕЛЮ.ОБЩИЙ ЗНАМЕНАТЕЛЬ ДРОБЕЙ – ЭТО ОБЩЕЕ КРАТНОЕ ЗНАМЕНАТЕЛЕЙ
(Чаще приводят дроби к наименьшему общему знаменателю, который равен НОК знаменателей данных дробей)
Слайд 189.9.17
Приведение дробей к общему знаменателю
Например: 5/6 и 3/4 привести к
общему знаменателю
1). Найдём НОК (6;4)
2). 12:6 = 2
3). 12:4 = 3 4). Числитель и знаменатель каждой дроби умножаем на дополнительный множитель этой дроби
= 12
(дополнительный множитель для первой дроби)
(дополнительный множитель для второй дроби)
Слайд 199.9.17
Приведение дробей к общему знаменателю
Чтобы привести дроби к наименьшему общему
знаменателю, надо:
найти НОК знаменателей данных дробей
найти дополнительные множители для каждой
дроби (для этого надо разделить общий знаменатель на знаменатель дроби)умножить числитель и знаменатель каждой дроби на дополнительный множитель этой дроби
Слайд 219.9.17
Сравнение дробей
Чтобы сравнить дроби с разными знаменателями, надо привести их
к общему знаменателю, а затем применить правило сравнения дробей с
одинаковыми знаменателями(т.е. та дробь будут больше, у которой числитель больше).
Слайд 229.9.17
Задание
Сравните дроби
Решение. 1) Приведём дроби к общему знаменателю
2) Найдём
дополнительные множители для каждой дроби: 15 : 3 =
5 (доп. множ. для первой дроби)15 : 5 = 3 (доп. множ. для второй дроби)
3) Получим дроби: и
4) Сравним
15
и делаем вывод.
Слайд 239.9.17
Задание
Расположите дроби в порядке возрастания
План решения:
1). Привести все дроби
к общему знаменателю
2). Получить дроби с одинаковым (общим)
знаменателем 3). Сравнить полученные дроби и выполнить задание
(30)
(24/30; 21/30; 16/30; 11/30)
Слайд 269.9.17
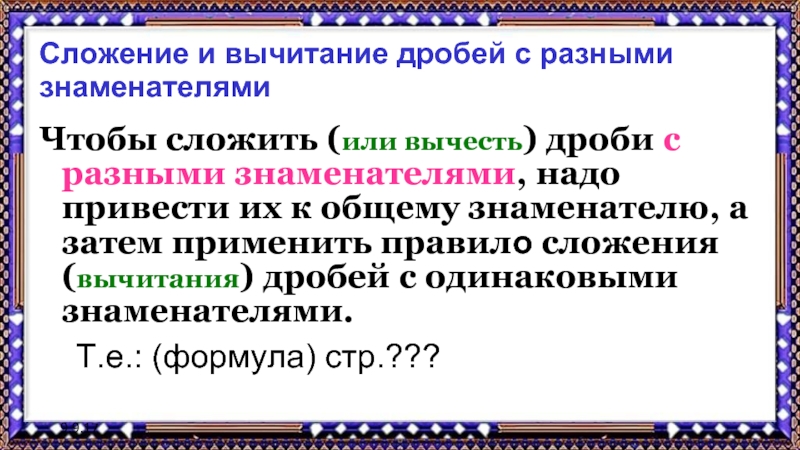
Сложение и вычитание дробей с разными знаменателями
Чтобы сложить (или вычесть)
дроби с разными знаменателями, надо привести их к общему знаменателю,
а затем применить правило сложения (вычитания) дробей с одинаковыми знаменателями.Т.е.: (формула) стр.???
Слайд 279.9.17
Сложение и вычитание дробей с разными знаменателями
Для дробей, как и
для натуральных чисел, выполняются свойства сложения:
Слайд 299.9.17
Сложение и вычитание смешанных чисел
ЧТОБЫ СЛОЖИТЬ ( или вычесть) СМЕШАННЫЕ
ЧИСЛА, НАДО:
ПРИВЕСТИ ДРОБНЫЕ ЧАСТИ ЭТИХ ЧИСЕЛ К НАИМЕНЬШЕМУ ОБЩЕМУ ЗНАМЕНАТЕЛЮ;
ОТДЕЛЬНО
ВЫПОЛНИТЬ СЛОЖЕНИЕ ( или вычитание) ЦЕЛЫХ ЧАСТЕЙ И ОТДЕЛЬНО – ДРОБНЫХ ЧАСТЕЙЕСЛИ ПРИ СЛОЖЕНИИ ДРОБНЫХ ЧАСТЕЙ ПОЛУЧИЛАСЬ НЕПРАВИЛЬНАЯ ДРОБЬ, ВЫДЕЛИТЬ ЦЕЛУЮ ЧАСТЬ ИЗ ЭТОЙ ДРОБИ И ПРИБАВИТЬ ЕЕ К ПОЛУЧЕННОЙ ЦЕЛОЙ ЧАСТИ.
Слайд 309.9.17
Сложение и вычитание смешанных чисел
ЕСЛИ ДРОБНАЯ ЧАСТЬ УМЕНЬШАЕМОГО МЕНЬШЕ ДРОБНОЙ
ЧАСТИ ВЫЧИТАЕМОГО, ТО НАДО ПРЕВРАТИТЬ ДРОБНУЮ ЧАСТЬ УМЕНЬШАЕМОГО В НЕПРАВИЛЬНУЮ
ДРОБЬ, УМЕНЬШИВ НА ЕДИНИЦУ ЦЕЛУЮ ЧАСТЬНапример (решаем вместе):
Слайд 329.9.17
Умножение дробей
Чтобы умножить дробь на дробь, надо числитель первой дроби
умножить на числитель второй дроби; знаменатель первой дроби умножить на
знаменатель второй дроби.Т.е.
Слайд 339.9.17
Умножение дробей
Для дробей, как и для натуральных чисел, выполняются свойства
умножения:
(
стр. 65 учебника )
Слайд 349.9.17
Обратим внимание
При умножении дробей не всегда надо спешить вычислить произведение
числителей и знаменателей, поскольку удобнее сначала выполнить сокращение (если это
возможно).Например
лучше сначала сократить :
Слайд 369.9.17
Взаимно обратные числа
Два числа (дроби), произведение которых равно 1, называются
взаимно обратными.
Например
Слайд 379.9.17
Умножение смешанных чисел
Чтобы умножить смешанные числа надо их записать в
виде неправильной дроби, а затем воспользоваться правилом умножения дробей.
Например
Слайд 399.9.17
Деление дробей
Чтобы разделить одну дробь на другую, надо делимое умножить
на число, обратное делителю.
Т.е.
Слайд 419.9.17
Деление смешанных чисел
Чтобы разделить смешанные числа надо их записать в
виде неправильной дроби, а затем воспользоваться правилом деления дробей.
Например
Слайд 439.9.17
Преобразование обыкновенной дроби в десятичную
Чтобы преобразовать обыкновенную дробь в десятичную,
надо числитель дроби разделить на её знаменатель.
Слайд 449.9.17
Преобразование обыкновенной дроби в десятичную
Чтобы преобразовать несократимую обыкновенную дробь в
десятичную, надо привести её к одному из знаменателей: 10, 100,
1000 и т.д.Несократимую обыкновенную дробь можно преобразовать в десятичную тогда и только тогда, когда разложение знаменателя дроби на простые множители содержит только множители 2 и 5
Слайд 459.9.17
Обратим внимание
При делении натурального числа на натуральное число можно получить:
- натуральное число
-
конечную десятичную дробь- бесконечную периодическую
десятичную дробь
Слайд 48Источники ресурса
Шаблон создан на основе клипарта рамки
http://abload.de/img/gzdeforumdnyas-png-ce32u4u.png
И возможностей программы Microsoft
PowerPoint 2016
Шаблон презентации подготовила учитель русского языка и литературы Тихонова Надежда
Андреевна, г. КостанайА.Г. Мерзляк и др., Математика: 6 класс: учебник для учащихся общеобразовательных организаций/ - 2-е изд., перераб. – М. : Вентана-Граф,2016.
https://data3.proshkolu.ru/content/media/pic/icon/3000000/2824000/2823051-1a9d966c.gif
https://data3.proshkolu.ru/content/media/pic/icon/3000000/2824000/2823051-1a9d966c.gif
http://u.900igr.net:10/datai/matematika/Naimenshee-obschee-kratnoe/0018-009-18.png
Теги
