Слайд 11.Повторяем правила дифференцирования
2. В чем состоит геометрический смысл производной?
3.В чем
состоит физический смысл производной?
4.Написать формулы дифференцирования.
5.Написать уравнения касательной
6.Какие точки называются
критическими?
7.В чем состоит необходимое условие экстремума?
8.В чем состоит достаточный признак существования экстремума?
9.Алгоритм отыскания наибольшего и наименьшего значений функции у= f(x), непрерывной на отрезке [a; b].
Слайд 2Алгоритм отыскания наибольшего и наименьшего значений функции у= f(x), непрерывной
на отрезке [a; b].
1.Найти f ‘(x).
2.Найти критические точки, т.е. где f 'x)=0
и f ‘(x) не существует, и отобрать из них те, что лежат внутри отрезка [a; b].
3.Вычислить значения функции y=f(x) в критических точках и на концах отрезка, и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции y=f(x) на отрезке [a;b], которые обозначают так:
max[a;b] y(x) и m in[a;b]y(x).
Слайд 31. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены
шесть точек: x1, x2, x3, x4, x5, x6. В скольких из этих точек производная функции f(x) отрицательна?
Слайд 42.На рисунке изображён график функции y=f(x). На оси абсцисс отмечены семь
точек: x1, x2, x3, x4, x5, x6, х7. . В скольких из этих точек производная функции f(x) положительна?
Слайд 53.На рисунке изображены график функции y=f(x) и касательная к нему в точке
с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Слайд 64.Найдите наименьшее значение функции y=x3−x2−8x+4 на отрезке [1; 7]
Слайд 75.На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на
отрезке [−3; 3].
Слайд 86.На рисунке изображён график функции y=f(x), определённой на интервале (− 9; 5). Найдите количество
точек, в которых производная функции f(x) равна 0.
Слайд 97.На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой
точке отрезка [2; 8] функция f(x) принимает наименьшее значение?
Слайд 108.На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество
точек минимума функции f(x), принадлежащих отрезку [− 6 ; 4].
Слайд 119.На рисунке изображён график функции y=f(x), определённой на интервале (− 6 ; 6). Найдите количество
решений уравнения f '(x)=0 на отрезке [− 4,5 ; 2,5].
Слайд 1210.Материальная точка движется прямолинейно по закону x(t)=16 t3−2 t2+6 t+250,
где x —
расстояние от точки отсчёта в метрах, t — время в
секундах, измеренное с момента начала движения. В какой момент времени
(в секундах) её скорость была равна 96 м/с?
Слайд 13Найдите силу F , действующую на материальную точку с массой
m , движущуюся прямолинейно по закону
х( t ) =5 t 3 - 4t 2 ,при t = 5.
= t2- 5 t+12,
где t- время в секундах. В
какой момент времени (в секундах) скорость движения «пробки» вулкана будет равна 15 м/с?
Слайд 15Зависимость численности популяции тигров задана формулой N(t)= 5 t3-4 t2+1.
Найдите прирост популяции в момент времени t = 3.
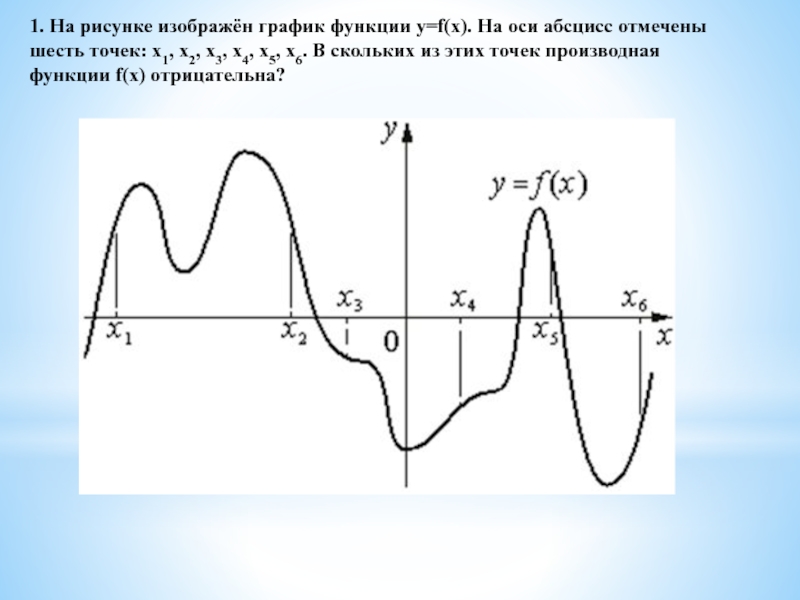
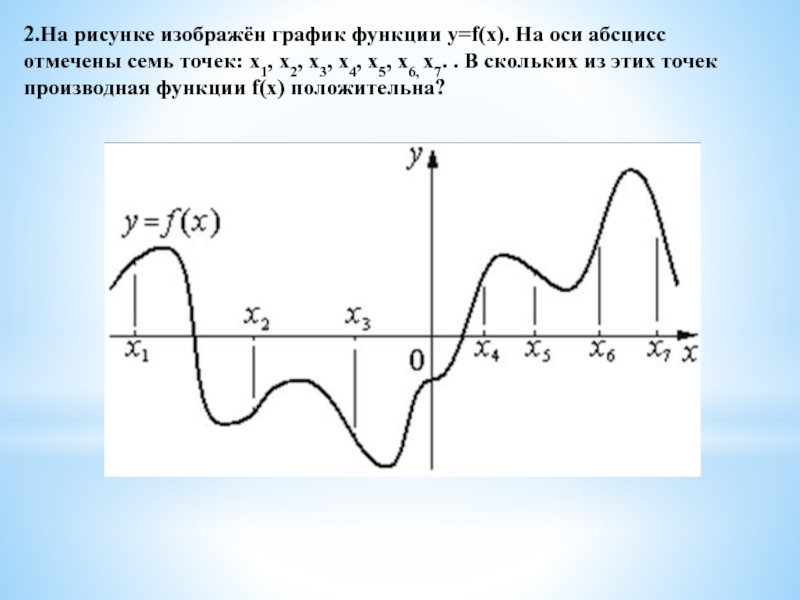
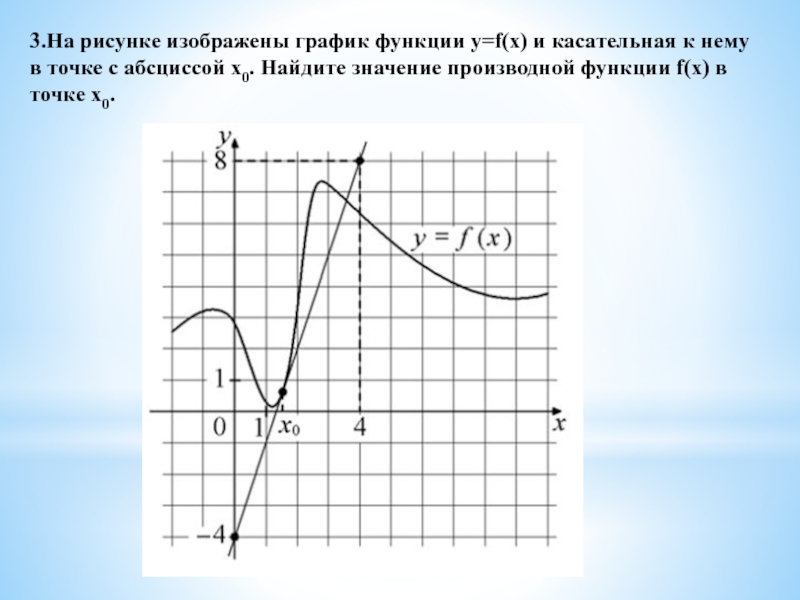
![Алгоритм отыскания наибольшего и наименьшего значений функции у= f(x), непрерывной на отрезке [a; b].1.Найти f ‘(x).2.Найти критические точки,](/img/thumbs/f00bf1bc8598a1c4937e6dd72c614f99-800x.jpg "Производная на ЕГЭ по математике Алгоритм отыскания наибольшего и наименьшего значений функции у= f(x), непрерывной на")
![4.Найдите наименьшее значение функции y=x3−x2−8x+4 на отрезке [1; 7]](/img/thumbs/e205ae59e4147c45b00cf9439f9b4feb-800x.jpg "Производная на ЕГЭ по математике 4.Найдите наименьшее значение функции y=x3−x2−8x+4 на отрезке [1; 7]")
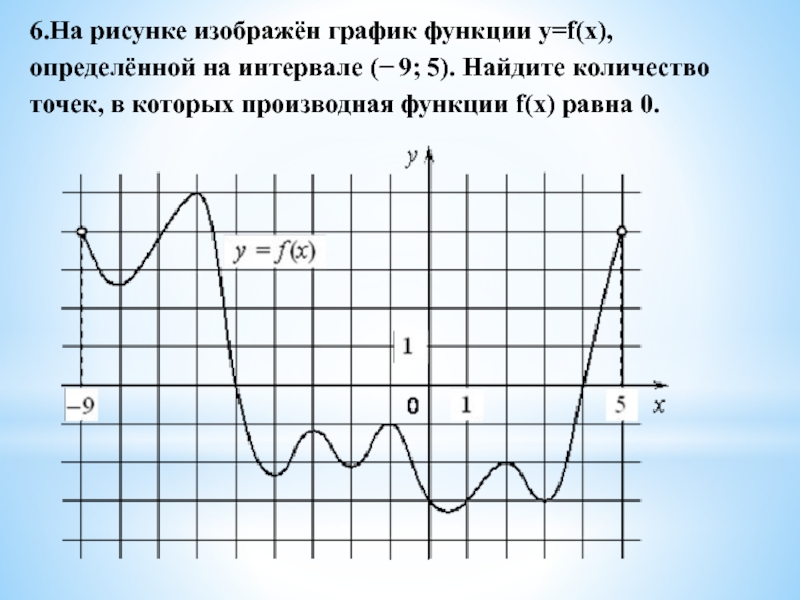
![5.На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].](/img/thumbs/339414b332501c683c10154824eab389-800x.jpg "Производная на ЕГЭ по математике 5.На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].")
![7.На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?](/img/thumbs/c3ffdaa254b8c4e71d17d4811d0fae8c-800x.jpg "Производная на ЕГЭ по математике 7.На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?")
![8.На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 6 ; 4].](/img/thumbs/81801fb79f0cebce01382df9a9ce59f8-800x.jpg "Производная на ЕГЭ по математике 8.На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 6 ; 4].")
![9.На рисунке изображён график функции y=f(x), определённой на интервале (− 6 ; 6). Найдите количество решений уравнения f '(x)=0 на отрезке [− 4,5 ; 2,5].](/img/thumbs/17f648ee4fb44b1c96a1979e22cb6316-800x.jpg "Производная на ЕГЭ по математике 9.На рисунке изображён график функции y=f(x), определённой на интервале (− 6 ; 6). Найдите количество решений уравнения f '(x)=0 на отрезке [− 4,5 ; 2,5].")
