Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока "Первый признак равенства треугольников".
Содержание
- 1. Презентация для урока "Первый признак равенства треугольников".
- 2. Треугольник (в евклидовом пространстве) — геометрическая фигура,
- 3. Два треугольника называются равными, если их можно
- 4. Теорема 1. Первый признак равенства треугольников. Если
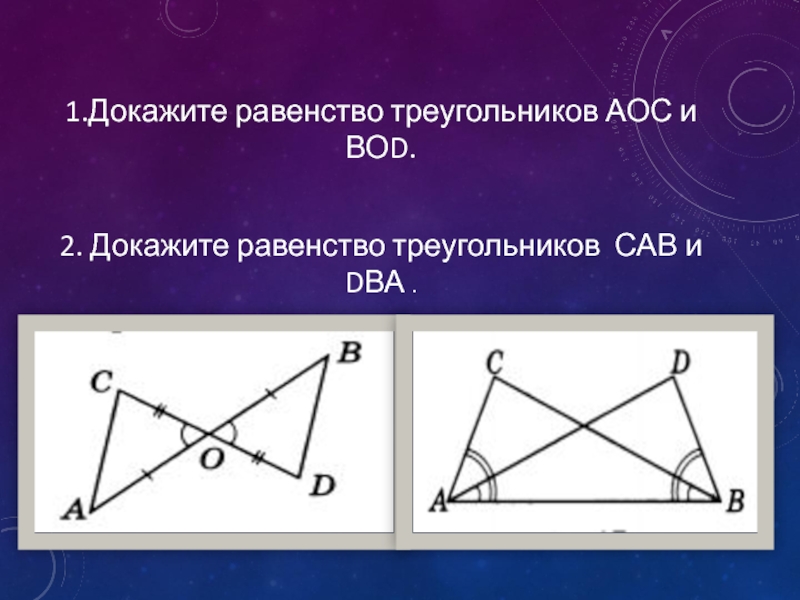
- 5. 1.Докажите равенство треугольников АОС и ВОD.2. Докажите равенство треугольников САВ и DВА .
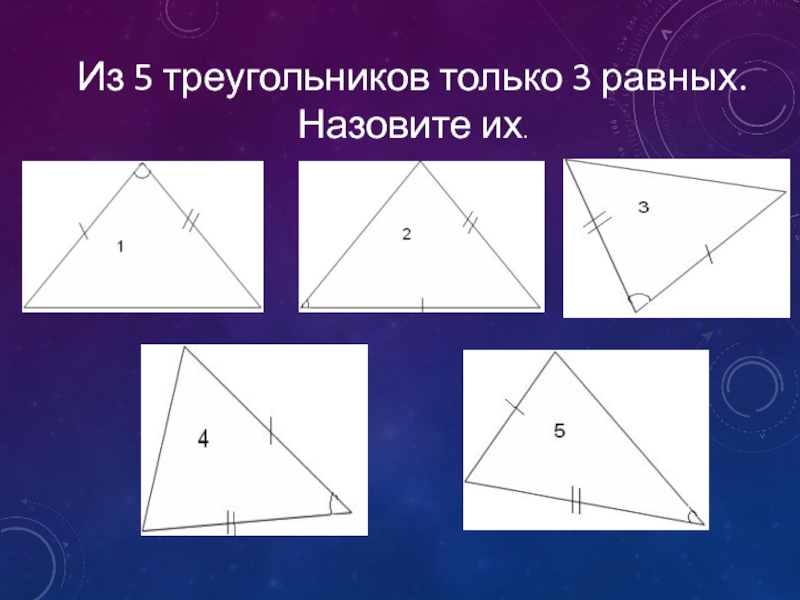
- 6. Из 5 треугольников только 3 равных. Назовите их.
- 7. Домашнее заданиеВыучить п.15, решить № 91,93.
- 8. Спасибо за внимание
- 9. Скачать презентанцию
Треугольник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны
Слайды и текст этой презентации
Слайд 2Треугольник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками,
Слайд 3Два треугольника называются равными, если их можно совместить наложением. На
рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из
этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А1В1 лежат равные углы С и С1. Равенство треугольников ABC и А1В1С1 будем обозначать так: Δ ABC = Δ А1В1С1. Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.