Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация квадратичная функция
Содержание
- 1. Презентация квадратичная функция
- 2. y= ax2 +bx + cгде: a,b,c –
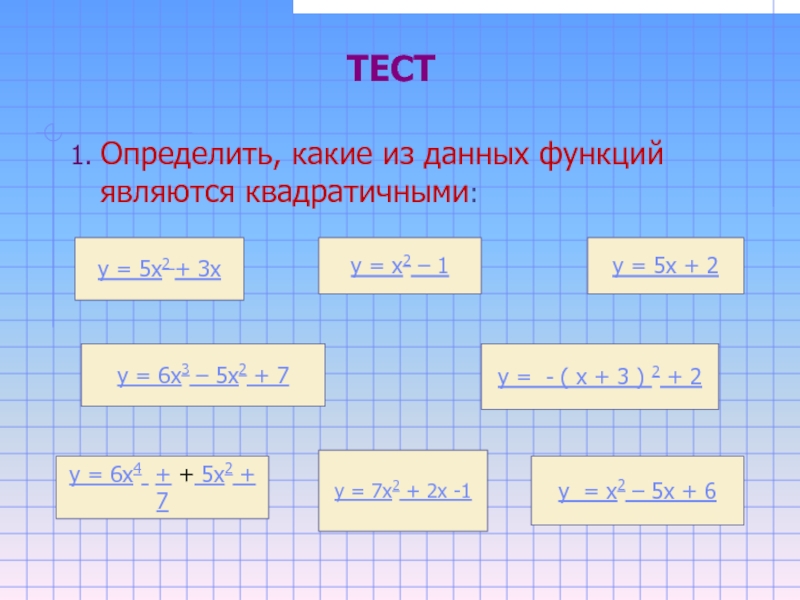
- 3. 1. Определить, какие из данных функций являются
- 4. Выберите правильный ответ:1.
- 5. Графиком квадратичной функции является:ГИПЕРБОЛАПРЯМАЯПАРАБОЛАВыберите правильный ответ:ПРОВЕРЯЕМ
- 6. Выберите график квадратичной функции1.2.3.ПРОВЕРЯЕМ
- 7. Выберите свойства для функции
- 8. Что можно сказать о количестве корней уравнения
- 9. На рисунках изображён график функции
- 10. Постройте график функции
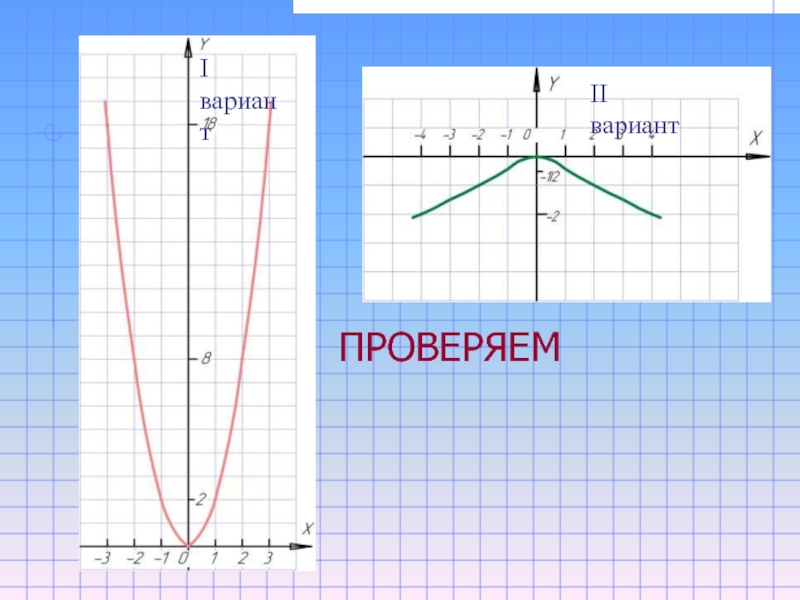
- 11. II вариант I вариант ПРОВЕРЯЕМ
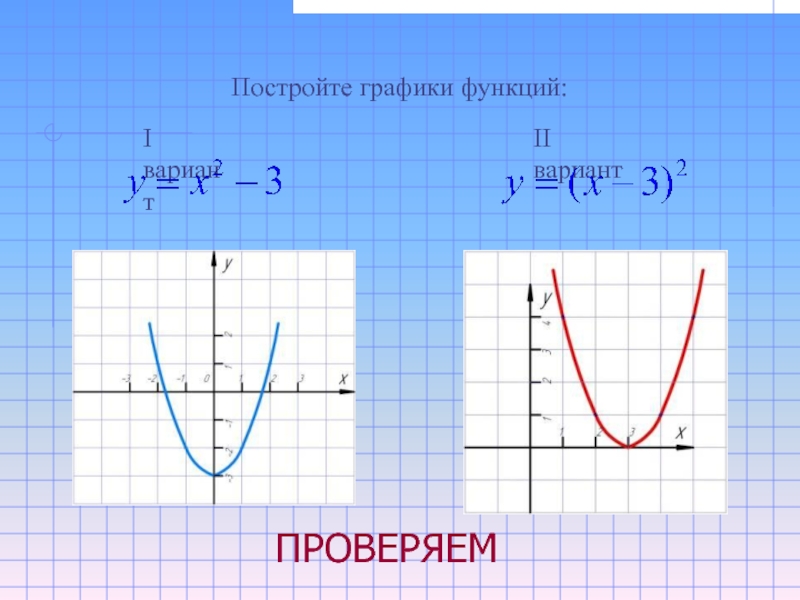
- 12. Постройте графики функций:I вариант II вариант ПРОВЕРЯЕМ
- 13. Запишите формулы вычисления координат вершины параболы.ПРОВЕРЯЕМ
- 14. Постройте график квадратичной функции
- 15. Вспоминаем : Дискриминантом квадратного уравнения ах2 +
- 16. если дискриминант больше нуля, то парабола
- 17.
- 18.
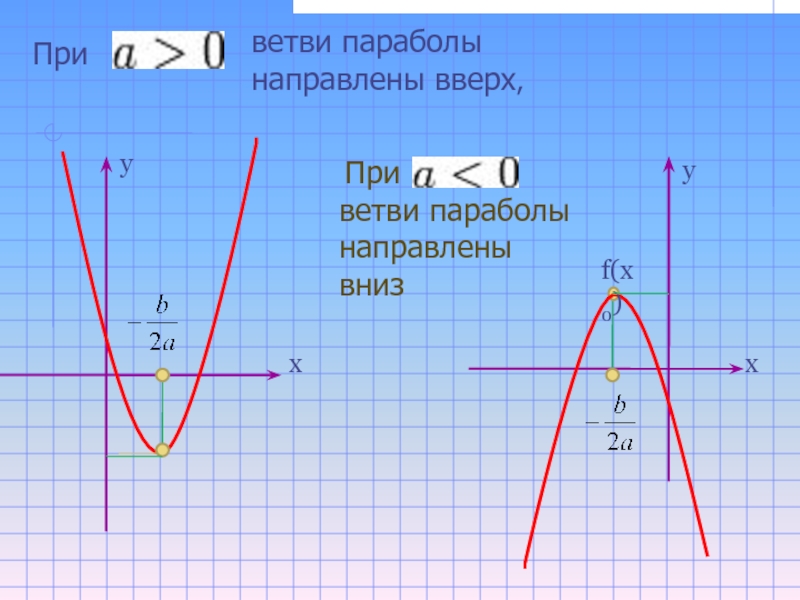
- 19. При - ветви параболы направлены вверх,При ветви параболы направлены внизf(x0)ххуу
- 20. Назовите те параболы,
- 21. Для закрепления теоретических знаний решим задачу.№ 264,265,266,267,268(1,2)
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2y= ax2 +bx + c
где: a,b,c – числа
Х –
независимая переменная
а
0Определение квадратичной функции
Квадратичной функцией называется функция , которую можно задать формулой вида:
Слайд 31. Определить, какие из данных функций являются квадратичными:
у = -
( х + 3 ) 2 + 2
у =
5х + 2у = х2 – 1
у = 6х3 – 5х2 + 7
у = 7х2 + 2х -1
у = 5х2 + 3х
ТЕСТ
у = х2 – 5х + 6
у = 6х4 + + 5х2 + 7
Слайд 4Выберите правильный ответ:
1.
где x - независимая переменная,
n-натуральное число.2.
где х - независимая переменная,
a,b,c – некоторые числа, причем а ≠0.
3.
где х – независимая переменная,
k, и – числа.
ПРОВЕРЯЕМ
Какая функция называется квадратичной?
Слайд 5Графиком квадратичной функции является:
ГИПЕРБОЛА
ПРЯМАЯ
ПАРАБОЛА
Выберите правильный ответ:
ПРОВЕРЯЕМ
Слайд 7Выберите свойства для функции
,
приЕсли х=0, то у=0. График проходит
через начало координат.
2. Функция убывает в промежутке [0;+∞)
и возрастает в промежутке (-∞;0].
3. Если х≠0, то y>0. График функции
расположен в верхней полуплоскости.
ПРОВЕРЯЕМ
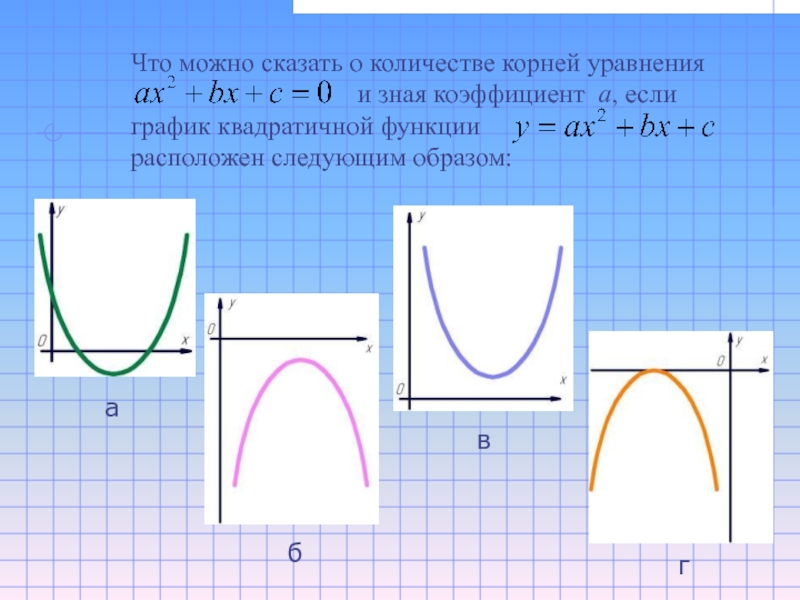
Слайд 8Что можно сказать о количестве корней уравнения
и зная коэффициент а, если
график квадратичной функции
расположен следующим образом:
а
б
в
г
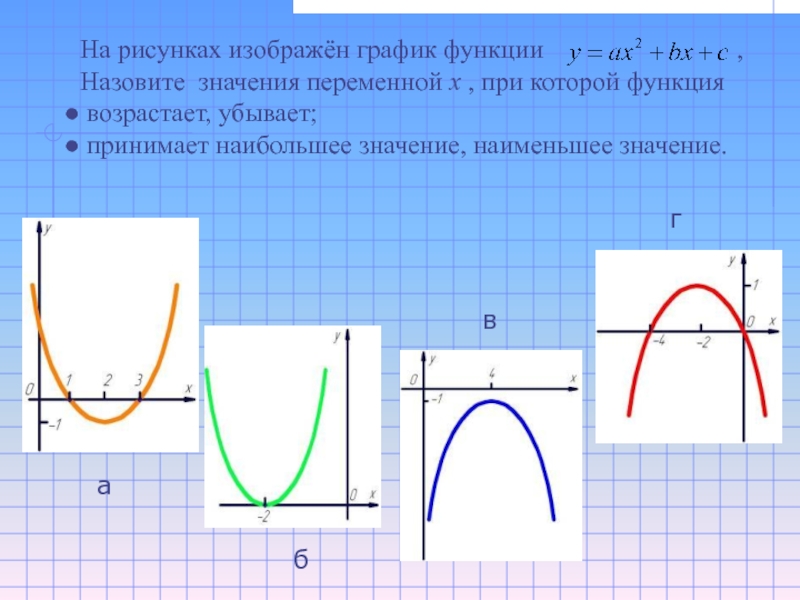
Слайд 9На рисунках изображён график функции
,
Назовите
значения переменной х , при которой функциявозрастает, убывает;
принимает наибольшее значение, наименьшее значение.
а
б
в
г
Слайд 15Вспоминаем :
Дискриминантом квадратного уравнения ах2 + bх + с
= 0 называется выражение
b2 – 4acЕго обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D > 0
D = 0
D < 0
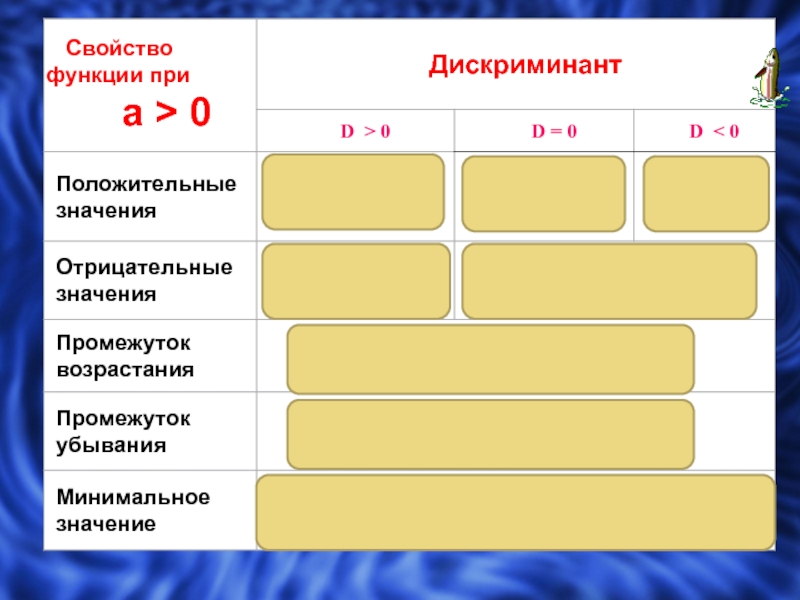
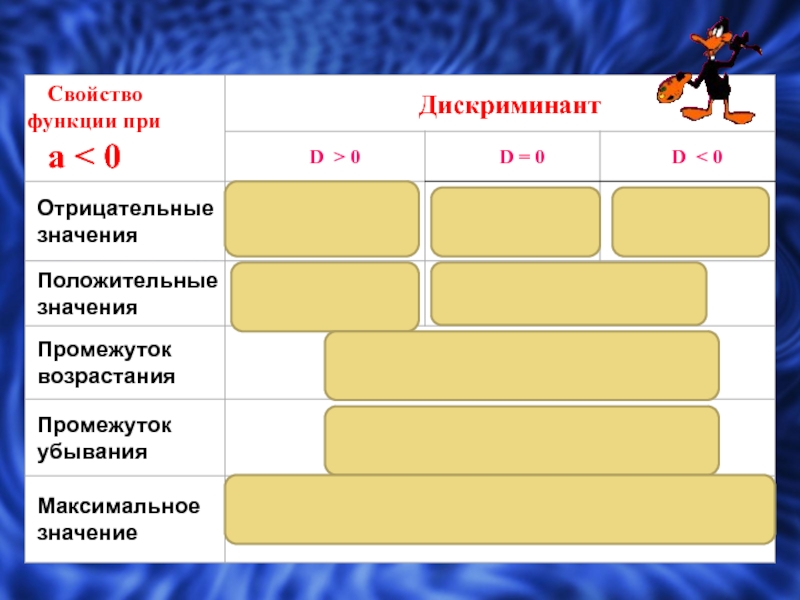
Слайд 16
если дискриминант больше нуля, то парабола пересекает ось абсцисс
в двух точках,
если дискриминант равен нулю, то парабола касается
оси абсцисс,если дискриминант меньше нуля, то парабола не пересекает ось абсцисс,
если старший коэффициент квадратного трёхчлена (а) равен нулю, то графиком функции является не парабола, а прямая; (и соответствующее уравнение надо решать не как квадратное, а как линейное),
абсцисса вершины параболы равна
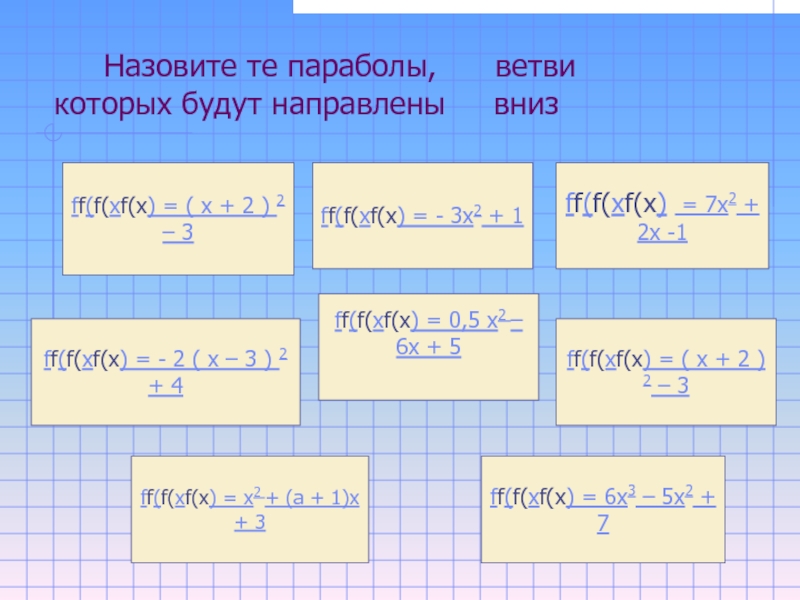
Слайд 20 Назовите те параболы, ветви которых
будут направлены вниз
ff(f(xf(x) = - 2 ( х
– 3 ) 2 + 4ff(f(xf(x) = 7х2 + 2х -1
ff(f(xf(x) = ( х + 2 ) 2 – 3
ff(f(xf(x) = х2 + (а + 1)х + 3
ff(f(xf(x) = 0,5 х2 – 6х + 5
ff(f(xf(x) = 6х3 – 5х2 + 7
ff(f(xf(x) = ( х + 2 ) 2 – 3
ff(f(xf(x) = - 3х2 + 1