Презентация "Методы решения тригонометрических уравнений" часть I

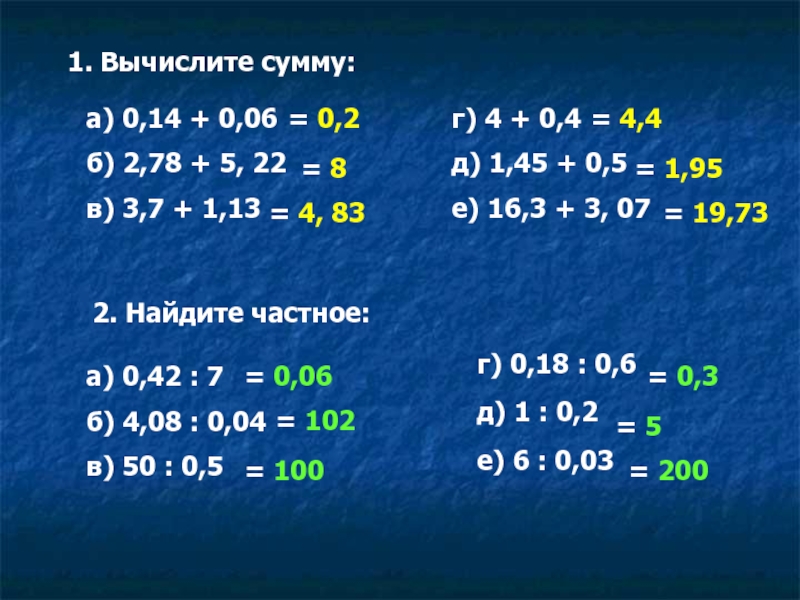
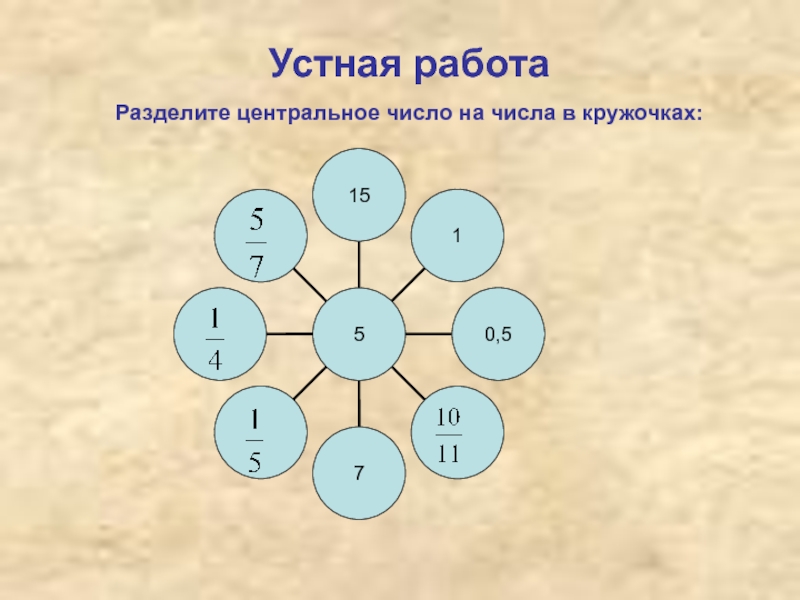
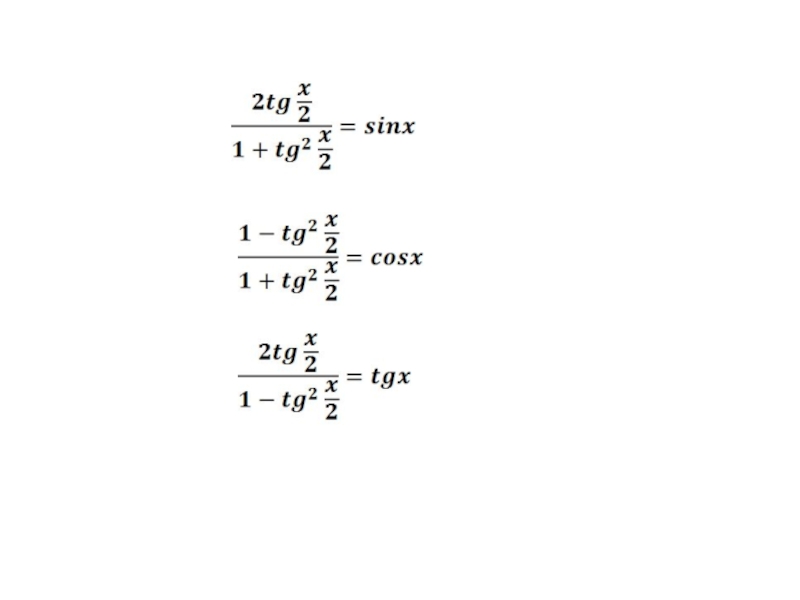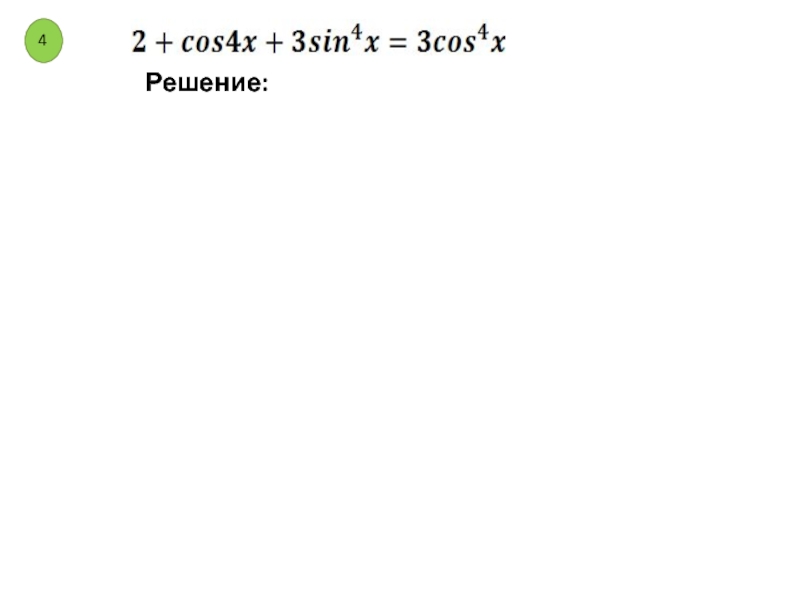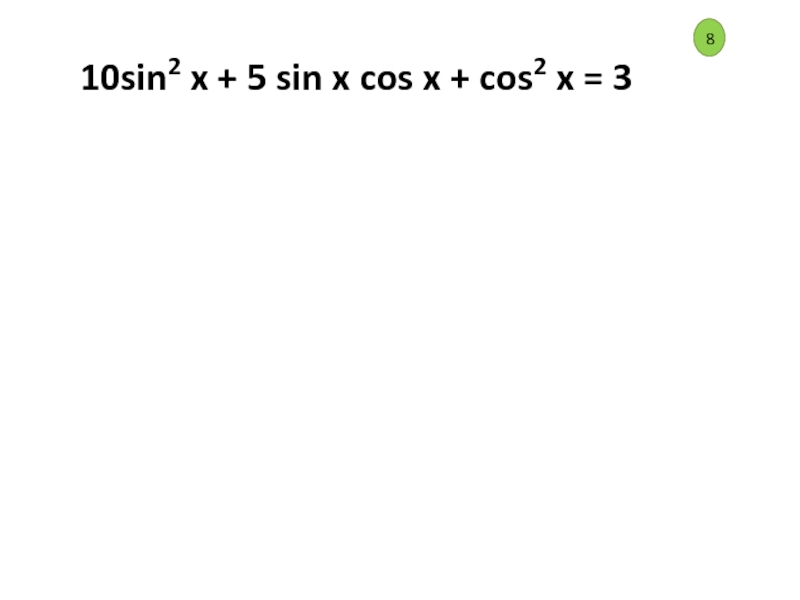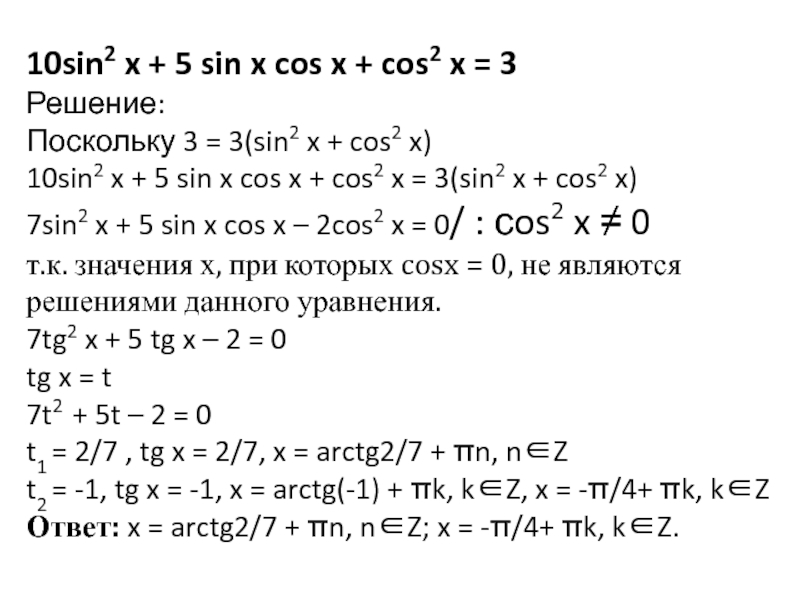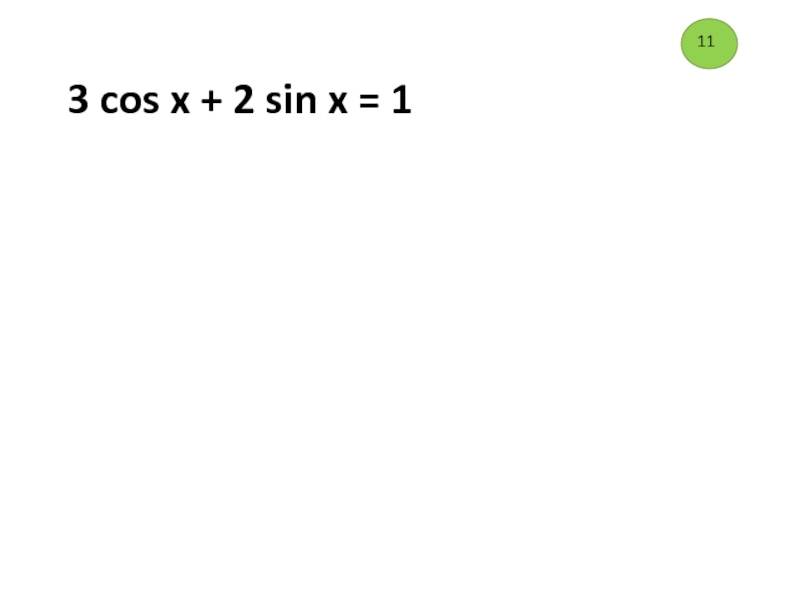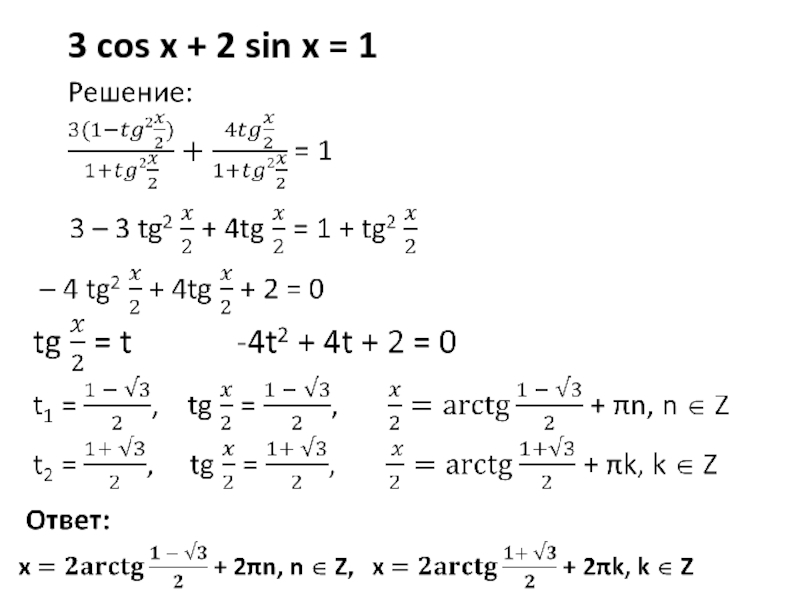множители,
замена переменной,
применение свойств функций,
а так же сочетание нескольких приёмов.

Основная

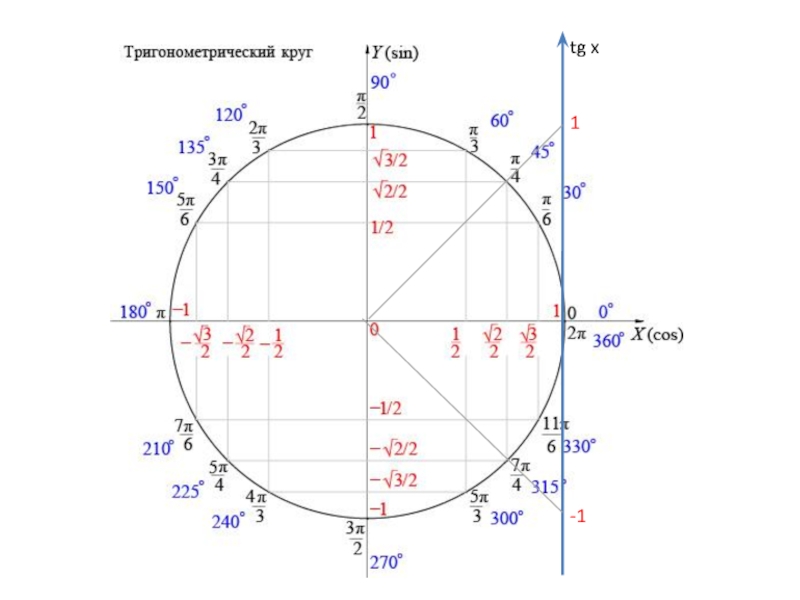
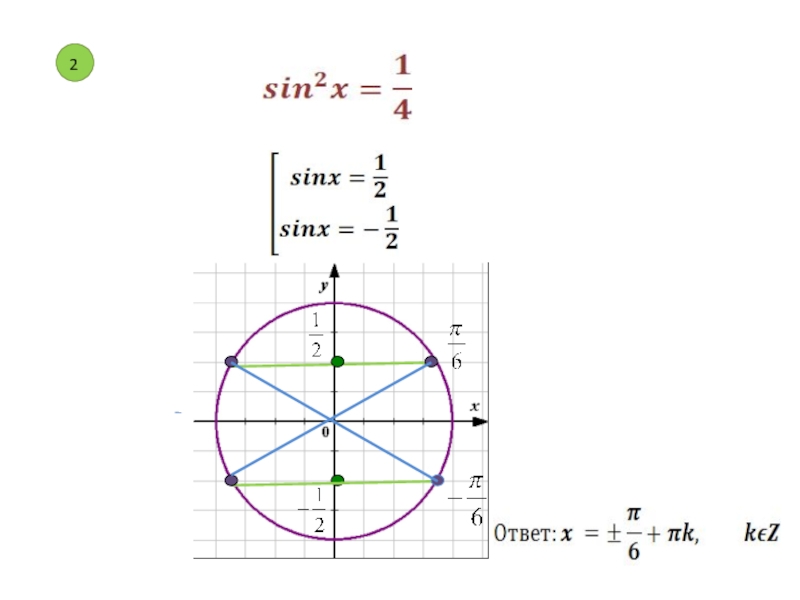
идея решения тригонометрического уравнения – сведение его к одному или нескольким простейшим уравнениям, т.е. уравнениям вида sin x = a, cos x = a,
tg x = a, ctg x = a.

 
 
- Применение основного тригонометрического тождества
cos2x + sin2x = 1
- Применение

формул удвоенного аргумента
sin2x = 2 sinx cosx cos2x = cos2x – sin2x

0 называют однородным тригонометрическим уравнением первой степени;
уравнение вида a

sin2x + b sinxcosx + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени.
Уравнения вида a sinmx + b cosmx = 0 также называются однородными тригонометрическими уравнениями первой степени.

Для однородных уравнений существует стандартный приём решения – деление обеих его частей на cosx ≠ 0 или cos2x ≠ 0.
Обоснованность деления:
Предположим, что cosx = 0. Тогда в силу уравнения и sinx = 0, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение этого уравнения удовлетворяет условию cosx ≠ 0, и мы можем поделить обе его части на cosx (cos2 x).

x = 3

8

x = 3
Решение:
Поскольку 3 = 3(sin2 x + cos2 x)
10sin2

x + 5 sin x cos x + cos2 x = 3(sin2 x + cos2 x)
7sin2 x + 5 sin x cos x – 2cos2 x = 0/ : сos2 x ≠ 0
т.к. значения х, при которых cosx = 0, не являются решениями данного уравнения.
7tg2 x + 5 tg x – 2 = 0
tg x = t
7t2 + 5t – 2 = 0
t1 = 2/7 , tg x = 2/7, x = arctg2/7 + πn, n∈Z
t2 = -1, tg x = -1, x = arctg(-1) + πk, k∈Z, x = -π/4+ πk, k∈Z
Ответ: x = arctg2/7 + πn, n∈Z; x = -π/4+ πk, k∈Z.

= π + 2πn n∈Z, поэтому данную серию нужно проверить

непосредственно подставив в уравнение.

a(sinx-cosx)+bsinxcosx+c=0
Замена:sinx+cosx=t