Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "четырехугольники"
Содержание
- 1. Презентация по теме "четырехугольники"
- 2. План проекта.1. Всё вокруг – геометрия2. Определение
- 3. Всё вокруг - геометрия.«Я думаю, что никогда,
- 4. Геометрия зародилась в глубокой древности. Строя жилища
- 5. ЧетырёхугольникиЧетырехугольником называется фигура, которая состоит из четырёх
- 6. СтихотворениеЧетырёхугольник фигурист,Состоит из точек и вершин,А его отрезки противолежащие Стороны же исходящие!!!
- 7. Генеалогическое древо четырёхугольников
- 8. Виды четырёхугольников
- 9. ПараллелограммЧетырёх угольник у которого противоположные стороны попарно
- 10. Диагонали параллелограмма делятся точкой пересечения пополам. Признаки
- 11. Так из первого признака получаем определения следующее
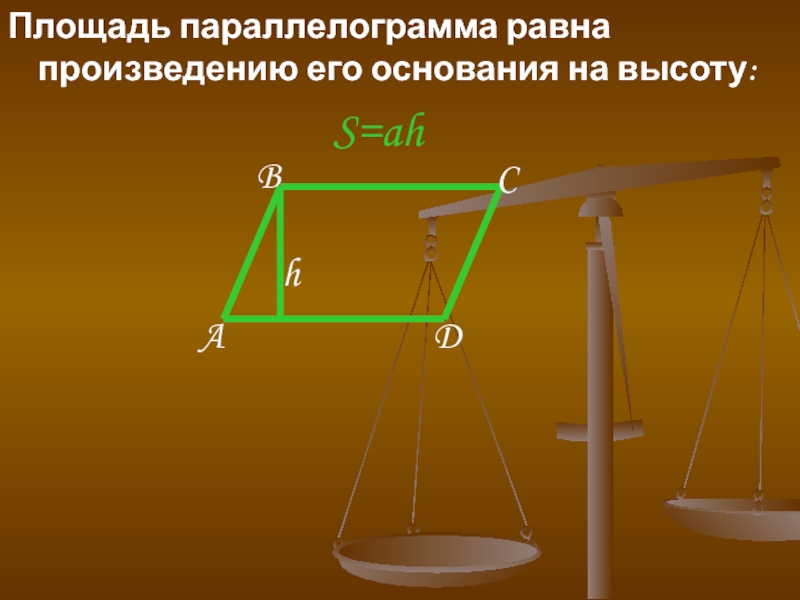
- 12. Площадь параллелограмма равна произведению его основания на
- 13. РомбПараллелограмм все стороны которого равны, называется площадь.
- 14. Площадь ромба может быть вычислена по формуле:
- 15. Прямоугольник Параллелограмм все углы, у которого прямые
- 16. Площадь прямоугольника вычисляется по формуле:
- 17. КвадратПрямоугольник у которого все стороны равны называется
- 18. СтихотворениеКвадрат поехал в ЛенинградИ там узнали про квадратЧто все сторонки равные Углы прямые, славные.
- 19. ТрапецияЧетырехугольник, две стороны которого параллельны, а две
- 20. В равнобедренной трапеции углы при основании равны:
- 21. Скачать презентанцию
План проекта.1. Всё вокруг – геометрия2. Определение четырёхугольника3. Стихотворение4. Генеалогическое древо5. Виды четырёхугольников6.Определение параллелограмма7. Определение ромба8. Определение прямоугольника9. Определение квадрата10.Стихотворение11. Определение трапеции
Слайды и текст этой презентации
Слайд 2План проекта.
1. Всё вокруг – геометрия
2. Определение четырёхугольника
3. Стихотворение
4. Генеалогическое
древо
Определение трапецииСлайд 3Всё вокруг - геометрия.
«Я думаю, что никогда, до настоящего времени,
мы не жили в такой геометрический период. Всё вокруг –
геометрия». Эти слова великого французского архитектора Ле Корбюзье очень точно характеризуют и наше время. Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нём, открывать новое, понимать красоту и мудрость окружающего мира поможет вам эта наука.Слайд 4Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая
их орнам6нтами, размечая территории на поверхности земли, измеряя расстояния и
площади зем6льных участков, человек применял свои знания о форме, размерах и взаимном расположении предметов, использовал свои геометричски5 знания, полученные из наблюдений и опытов. Почти все учёные древности и средних веков были выдающимися геометрами.Геометрия изучает форму и взаимное расположение фигур.
Слайд 5Четырёхугольники
Четырехугольником называется фигура, которая состоит из четырёх сторон и четырёх
последовательно соединяющих их отрезков.
Вершины четырёхугольника называются соседними, если они являются
концами одной из его сторон.Вершины, не являющихся соседними, называют противолежащими.
Стороны четырёхугольника, исходящие из одной вершины, называются соседними сторонами.
Отрезки, соединяющие противоположные вершины четырехугольника называют диагоналями.
Слайд 6Стихотворение
Четырёхугольник фигурист,
Состоит из точек и вершин,
А его отрезки противолежащие
Стороны
же исходящие!!!
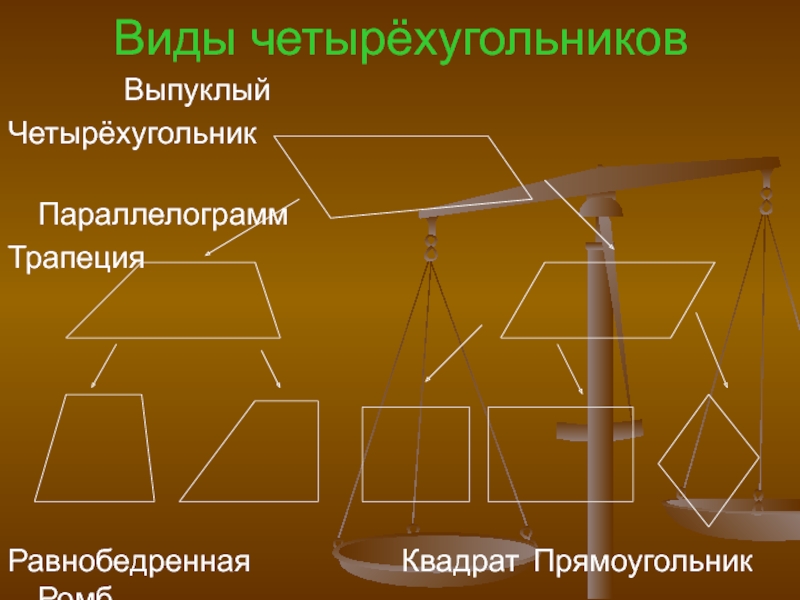
Слайд 8Виды четырёхугольников
Выпуклый
Четырёхугольник
Параллелограмм
Трапеция
Равнобедренная Квадрат Прямоугольник Ромб
Прямоугольная
Слайд 9Параллелограмм
Четырёх угольник у которого противоположные стороны попарно параллельны, называются параллелограммом.
Свойства
параллелограмма:
Противоположные стороны равны;
Противоположные углы параллелограмма равны;
Каждая диагональ параллелограмма делит его
на два равных треугольника; Слайд 10Диагонали параллелограмма делятся точкой пересечения пополам.
Признаки параллелограмма:
Если в четырёхугольнике
противоположные стороны попарно равны, то этот четырёх угольник-параллелограмм.
Если в четырёхугольнике
две противоположные стороны равны и параллельны, то этот четырёхугольник-параллелограмм.Каждый из признаков параллелограмма может быть взят в качестве определения параллелограмма.
Слайд 11Так из первого признака получаем определения следующее параллелограмма.
Четырёх угольник, у
которого противоположные стороны попарно равны, называется параллелограммом.
Сумма внутренних углов параллелограмма
равна 360°.
Отрезок перпендикуляра к сторонам параллелограмма, заключённый между ними, называется высотой параллелограмма.
Слайд 13Ромб
Параллелограмм все стороны которого равны, называется площадь. Помимо всех свойств
параллелограмма, ромб обладает следующими специальными свойствами:
Диагонали ромба взаимно перпендикулярны;
Диагонали ромба
являются биссектрисами его внутренних углов.Диагонали ромба делят его внутринии углы пополам.
Слайд 15Прямоугольник
Параллелограмм все углы, у которого прямые называется прямоугольник.
Помимо всех
свойств параллелограмма, прямоугольник обладает следующими специальными свойствами:
Диагонали прямоугольника равны.
Признаки прямоугольника:
Если
в параллелограмме диагонали равны, то этот параллелограмм-прямоугольник.Слайд 17Квадрат
Прямоугольник у которого все стороны равны называется квадратом.
Из определения квадрата
и ромба следует, что квадрат это ромб у которого все
углы прямые. Так как квадрат является и параллелограммом, и прямоугольником, и ромбом, то все свойства этих фигур присущи и квадрату.Площадь квадрата вычисляется по формуле:
S=a²
a
a
a
a
Слайд 18Стихотворение
Квадрат поехал в Ленинград
И там узнали про квадрат
Что все сторонки
равные
Углы прямые, славные.
Слайд 19Трапеция
Четырехугольник, две стороны которого параллельны, а две другие не параллельны,
называется трапецией.
Паралельные стороны трапеции называют её основаниями, а не паралельные
боковыми сторонами (ВС и АД-основания, АВ и СД-боковые стороны)Отрезок перпендикуляра к основаниям трапеции, заключённый между основаниями называется высотой трапеции (ВН- высота). Трапеция, боковые стороны которой равны называется равнобедренной (или равнобочной).
В
А
С
Д
Н
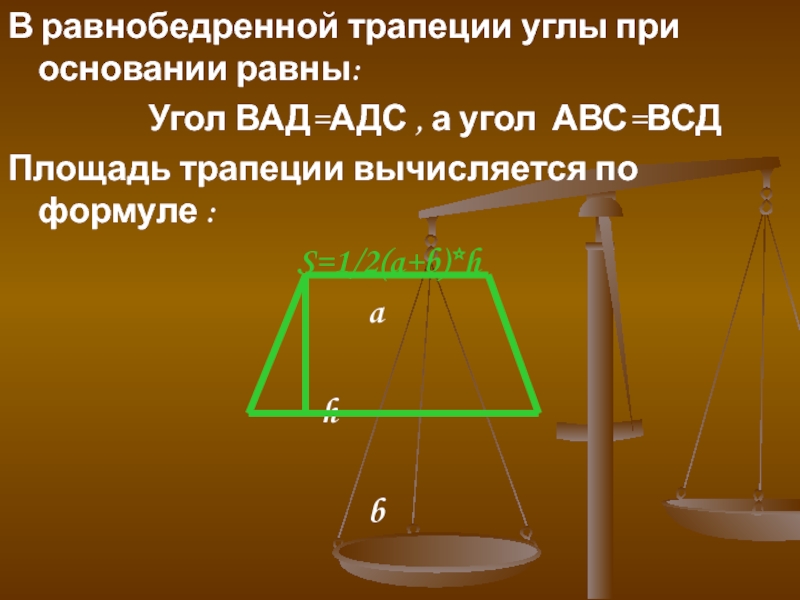
Слайд 20В равнобедренной трапеции углы при основании равны:
Угол ВАД=АДС , а угол
АВС=ВСДПлощадь трапеции вычисляется по формуле :
S=1/2(a+b)*h
a
h
b