Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация решения задач ОГЭ модуль геометрия.
Содержание
- 1. Презентация решения задач ОГЭ модуль геометрия.
- 2. Задание 9.
- 3. Задание 10.
- 4. Задание 11.
- 5. Задание 12.Для того, что бы найти S
- 6. Задание 13.1) Верно (Любые два равносторонних треугольника
- 7. Задание 17
- 8. Задание 24.АВСОДано: AB=2, AC=8Найти: диаметр окружностиРешение: OC – радиус окружности. АО=АС-ОС Проведём отрезок ОВ,
- 9. Задание 25.АВСDДано:
- 10. Скачать презентанцию
Задание 9. Дано: △ABC прямоугольный,
Слайды и текст этой презентации
Слайд 2Задание 9.
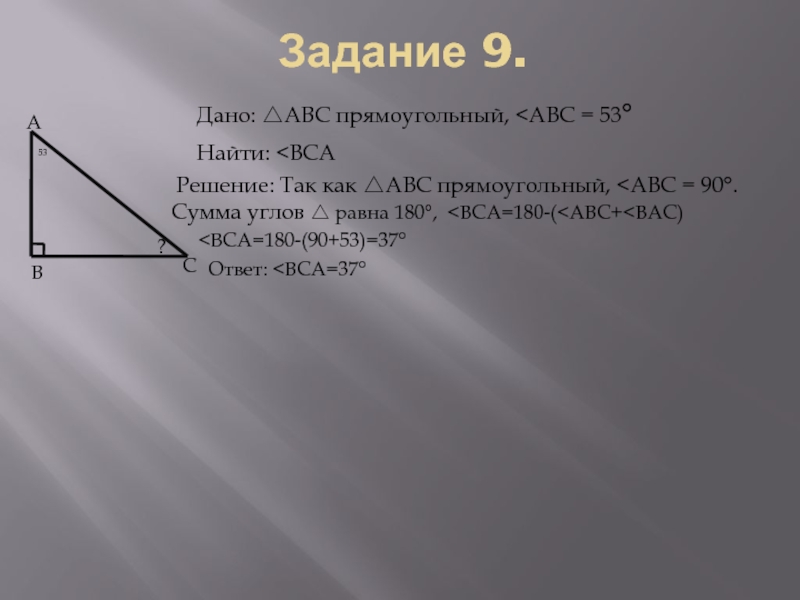
Дано: △ABC прямоугольный,
Найти: <ВСАРешение: Так как △АВС прямоугольный, <АВС = 90°. Сумма углов △ равна 180°, <ВСА=180-(<АВС+<ВАС)
<ВСА=180-(90+53)=37°
Ответ: <ВСА=37°
53
?
А
В
С
Слайд 3Задание 10.
Дано: Четырёхугольник ABCD вписан в окружность,
Решение: По теореме вписанный угол измеряется половиной дуги, на которую он опирается, значит дуга в 2 раза больше угла, на который она опирается. Так как
А
В
С
D
Слайд 4Задание 11.
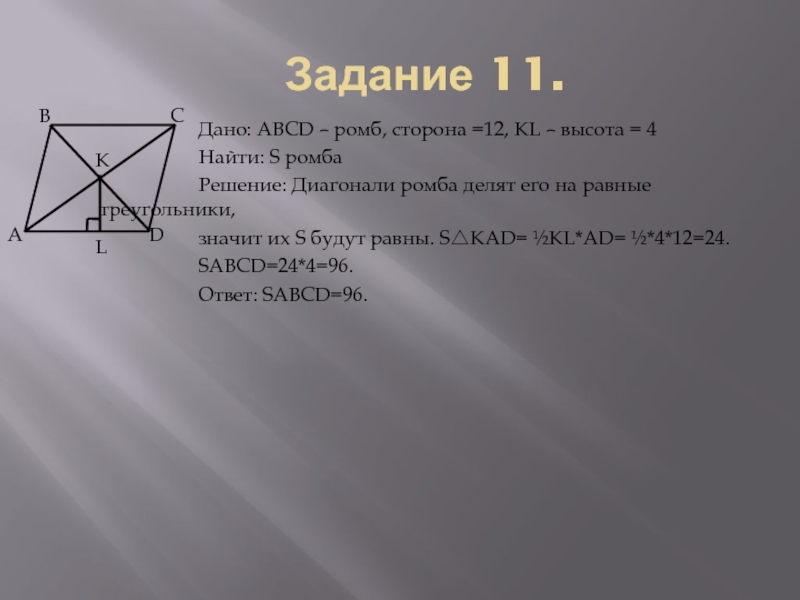
Дано: ABCD – ромб, сторона
=12, KL – высота = 4Найти: S ромба
Решение: Диагонали ромба делят его на равные треугольники,
значит их S будут равны. S△KAD= ½KL*AD= ½*4*12=24.
SABCD=24*4=96.
Ответ: SABCD=96.
А
В
С
D
K
L
Слайд 5Задание 12.
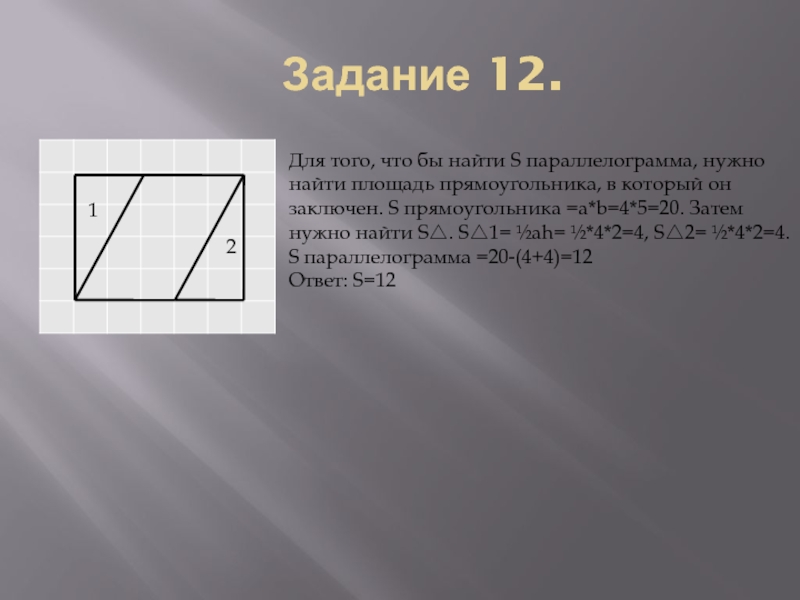
Для того, что бы найти S параллелограмма, нужно найти
площадь прямоугольника, в который он заключен. S прямоугольника =a*b=4*5=20. Затем
нужно найти S△. S△1= ½аh= ½*4*2=4, S△2= ½*4*2=4. S параллелограмма =20-(4+4)=12Ответ: S=12
1
2
Слайд 6Задание 13.
1) Верно (Любые два равносторонних треугольника подобны)
2) Не верно
(В любом прямоугольнике диагонали взаимно перпендикулярны)
3) Верно ( Все диаметры
окружности равны между собой)Слайд 8Задание 24.
А
В
С
О
Дано: AB=2, AC=8
Найти: диаметр окружности
Решение: OC – радиус окружности.
АО=АС-ОС Проведём отрезок ОВ,
конец радиуса. По теореме Пифагора: АО²=АВ²+ОВ²(АС-ОС)²=АВ²+R²; (8-R)²=2²+R²; 64-16R+R²=4+R²;
-16R=-60
R=3.75 D=3,75∙2=7,5
Ответ: D=7.5
Слайд 9Задание 25.
А
В
С
D
Дано:
подобны, так как
О точка пересечения диагоналей , т.к. ∆ подобны то сходственные стороны пропорциональны т.е. АО∙ОС=ОD∙ВОЗначит ∆ВОС~∆АОD по вертикальным углам <ВОС=<АОDи пропорциональным сторонам АО∙ОС=ОD∙ВО. Из подобия ∆ АDО и ВСО следует равенство углов <ВDА=<ВСА
O