Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация урока "О производной."
Содержание
- 1. Презентация урока "О производной."
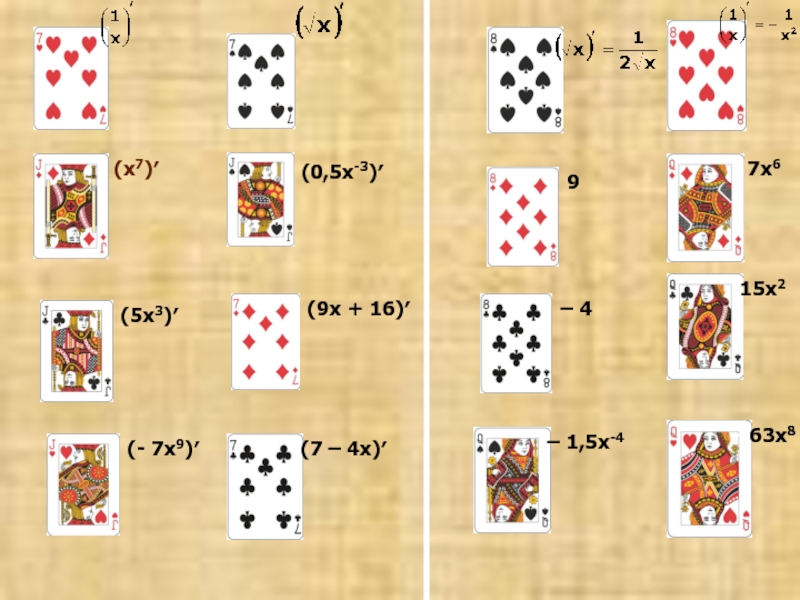
- 2. Сойдётся ли наш пасьянс в проведении урока?
- 3. (х7)′(5х3)′(- 7х9)′(0,5х-3)′(9х + 16)′(7 – 4х)′
- 4. История появления термина «производная»
- 5. «Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет» Лейбниц Готфрид Фридрих
- 6. Раздел математики который изучает производные функции и
- 7. Ряд задач дифференциального исчисления был решен еще
- 8. Аполлоний – к эллипсу, гиперболе и параболе.
- 9. Более общим и важным для развития дифференциального
- 10. Задача нахождения скорости изменения функции была
- 11. Основываясь на результатах Ферма и некоторых других
- 12. Термин «производная» впервые встречается у француза Луи
- 13. Применение производной:Мощность – это производная
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. В математике есть своя красота, как в живописи и поэзии.Кому принадлежат эти строки?Попробуем расшифровать.
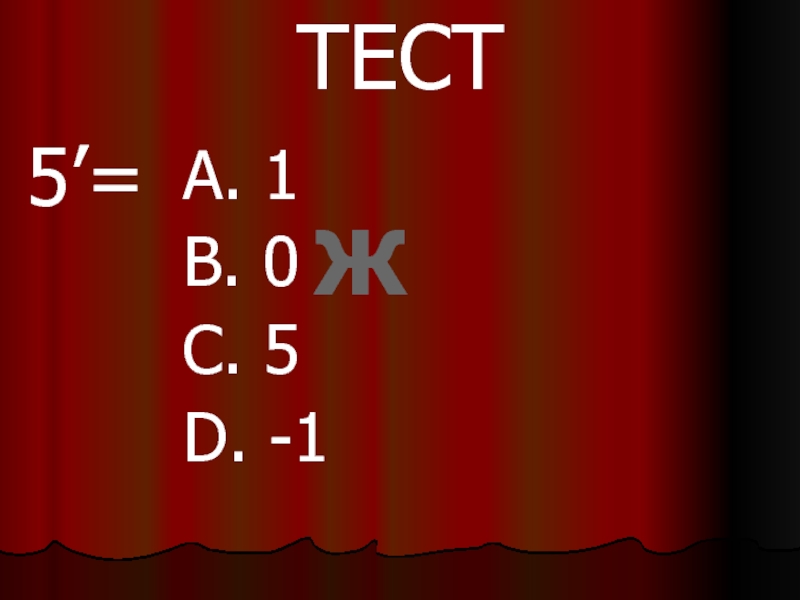
- 20. ТЕСТ5’=A. 1B. 0C. 5D. -1Ж
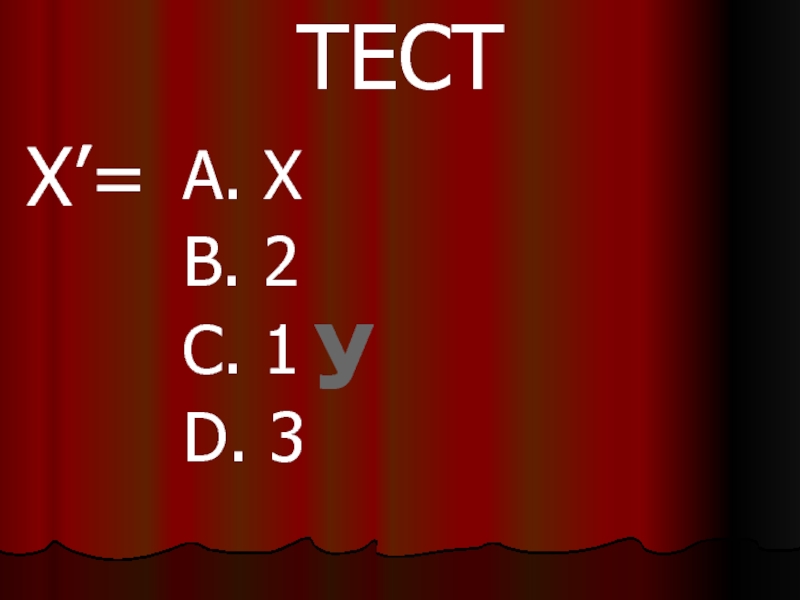
- 21. ТЕСТX’=A. XB. 2C. 1D. 3У
- 22. ТЕСТ(3X2)’=A. 2XB. 6XC. 3X2D. 3К
- 23. ТЕСТ(X-X2)’=A. 2XB. X-X2C. 1-2XD. 1-X2O
- 24. ТЕСТ(X10)’=A. 10X9B. 10X10C. 0D. 2XB
- 25. ТЕСТ(sinX)’=A. tgXB. XC. cosXD. sinXC
- 26. ТЕСТ(5X+8)’=A. 8B. 5XC. 8XD. 5K
- 27. ТЕСТ(eX)’=A. eXB. XC. 1D. lnXИ
- 28. ТЕСТ(π-X)’=A. πB. XC. 1D. -1Й
- 29. ЖУКОВСКИЙ ВАСИЛИЙ АНДРЕЕВИЧ(1783-1852)
- 30. В математике есть своя красота, как в живописи и поэзии.
- 31. Из букв в слове «ПРОИЗВОДНАЯ» составьте слова, как можно больше.
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 6Раздел математики который изучает производные функции и их применения, называется
дифференциальным исчислением. Это исчисление возникло из решений задач на проведение
касательных к кривым, на вычисление скорости движения, на отыскание наибольших и наименьших значений функции.Слайд 7Ряд задач дифференциального исчисления был решен еще в древности Архимедом,
разработавшим способ проведения касательной.
Архимед построил касательную к спирали, носящей его
имя. Архимед (ок. 287 – 212 до н.э.) – великий ученый. Первооткрыватель многих фактов и методов математики и механики, блестящий инженер.
Слайд 8
Аполлоний – к эллипсу, гиперболе и параболе.
Но общего метода,
пригодного для построения касательной к любой кривой плоскости в произвольной
ее точке найдено не было.
Слайд 9Более общим и важным для развития дифференциального исчисления был метод
построения касательных Ферма.
Пьер Ферма (1601 – 1665 гг.) – французский
математик и юристСлайд 10 Задача нахождения скорости изменения функции была впервые решена Ньютоном.
Функцию он назвал флюэнтой, т.е. текущей величиной. Производную –
ф л ю к с и е й.Ньютон пришел к понятию производной исходя из вопросов механики.
Исаак Ньютон (1643 – 1722 гг.) – английский физик и математик.
Слайд 11Основываясь на результатах Ферма и некоторых других выводах, Лейбниц в
1684 году
опубликовал первую статью по дифференциальному исчислению, в которой были
изложены основные правила дифференцирования.Лейбниц Готфрид Фридрих (1646 – 1716) – великий немецкий ученый, философ, математик, физик, юрист, языковед
Слайд 12 Термин «производная» впервые встречается у француза Луи Арбогаста. Этим термином
стал пользоваться Лагранж, который и ввел обозначения
У’ и F’(X).
Лагранж,
Жозеф (1736–1813), французский математик и механик.Слайд 13 Применение производной:
Мощность – это производная работы по времени
P = A'
(t).Сила тока – производная от заряда по времени I = g' (t).
Сила – есть производная работы по перемещению F = A' (x).
Теплоемкость – это производная количества теплоты по температуре C = Q' (t).
Давление – производная силы по площади P = F'(S)
Длина окружности – это производная площади круга по радиусу lокр=S'кр(R).
Темп роста производительности труда – это производная производительности труда по времени.
Успехи в учебе? Производная роста знаний.