Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проект по теме: "Золотое сечение"
Содержание
- 1. Проект по теме: "Золотое сечение"
- 2. Слайд 2
- 3. Геометрия владеет двумя сокровищами -теоремой Пифагора
- 4. Давайте выясним, что общего между древнеегипетскими
- 5. 1. Познакомить учащихся с примерами Золотого
- 6. В чем заключается гармония окружающего нас мира?Золотое сечение
- 7. Золотое сечение
- 8. История золотого сечения
- 9. Замечательный пример «золотого сечения» представляет собой правильный
- 10. С историей золотого сечения связано имя итальянского
- 11. Золотое сечение в живой
- 12. между каждыми двумя парами листьев третья расположена в месте золотого сечения
- 13. У многих бабочек соотношение размеров грудной и
- 14. В ящерице с первого взгляда улавливаются приятные
- 15. Спираль Архимеда Спираль - довольно изящная кривая.
- 16. Лежащее в основе строения спирали правило золотого
- 17. Священный холм и храм Божественной Афины, Великолепный
- 18. Храм Парфенон Парфенон имеет 8
- 19. По каким математическим законам созданы мировые шедевры архитектуры и скульптуры?
- 20. Золотое сечение в живописи
- 21. Личность Леонардо да Винчи– одна из загадок
- 22. Портрет Монны Лизы (Джоконды) долгие годы привлекает
- 23. Золотое сечение в живописиКартина или фотография имеет
- 24. Картина Шишкина На этой знаменитой
- 25. Золотое сечение в скульптуреСкульпторы утверждают, что талия
- 26. Великий древнегреческий скульптор Фидий часто использовал “золотое
- 27. Шедевром красоты считаетсяАфродита Милосская,созданная Агесандром.Это о ней
- 28. Золотое сечение в
- 29. Золотое сечение в других частях тела
- 30. Измеряем рост
- 31. Измеряем длину плеча, предплечья и кисти
- 32. Слайд 32
- 33. Что такое «золотое сечение»?.. Что это за
- 34. Спасибо за внимание !
- 35. Скачать презентанцию
На Земле, как и во всей Вселенной, дают о себе знать удивительный порядок и
Слайды и текст этой презентации
Слайд 1Работу выполнили : учащиеся 11 класса МОУ Р-Буйловской СОШ Руководитель проекта: учитель математики
Чернова Е.Н.
Слайд 2 На Земле,
как и во всей Вселенной, дают
о себе знать удивительный порядок и совершенная гармония.Слайд 3Геометрия владеет двумя сокровищами -теоремой Пифагора и золотым сечением. И если первое
из этих двух сокровищ можно сравнить с мерой золота, то
второе с драгоценным камнем. Иоганн KеплерСлайд 4Давайте выясним,
что общего между древнеегипетскими пирамидами, картиной
Леонардо да Винчи "Мона Лиза", подсолнухом, улиткой, сосновой шишкой и
пальцами человека?Слайд 5
1. Познакомить учащихся с примерами Золотого сечения в окружающем
мире; 2. Повысить мотивацию к обучению, развить логическое мышление учащихся; 3.
Сформировать навыки познавательной и практической деятельности при оформлении проектной работы; 4.Сделать вывод о математическом представлении нашего мира 5. Оформить в виде презентации .Цели проекта
Слайд 7
Золотое сечение – это такое пропорциональное деление отрезка на
неравные части, при котором меньший отрезок так относится к большему,
как больший ко всему.a : b = b : c
b ≈ 0,62..., a ≈ 0,38....
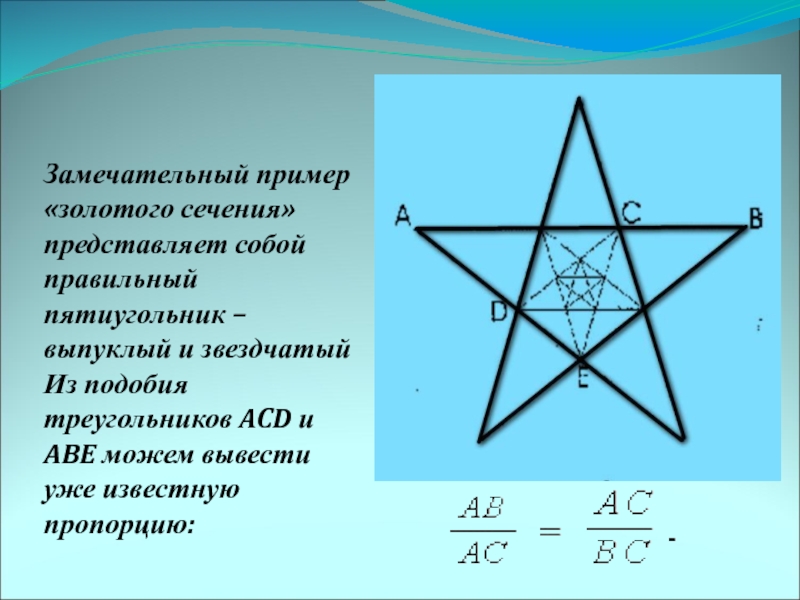
Слайд 9Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый
и звездчатый Из подобия треугольников ACD и ABE можем вывести
уже известную пропорцию:Слайд 10С историей золотого сечения связано имя итальянского математика Леонардо из
Пизы, более известного под именем Фибоначчи
0+1=1,
1+1=2,
2+1=3,
2+3=5 и
т.д., 34: 55=0,618…;
21:34=0, 617…;
13:21=0,619… и т.д.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …..
Слайд 13У многих бабочек соотношение размеров грудной и брюшной части тела
отвечает золотой пропорции. Стрекоза также создана по законам золотой пропорции:
отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.Слайд 14В ящерице с первого взгляда улавливаются приятные для нашего глаза
пропорции –
длина ее хвоста так относится к длине
остального
тела, как
62 к 38
Можно также заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.
Слайд 15Спираль Архимеда
Спираль - довольно
изящная кривая.
Первым внимание на неё
обратил древнегреческий
ученый Архимед,
имя которого она и носит. Он
изучал и вывел её уравнение. Увеличение ее шага всегда равномерно и соответствует золотому сечениюСлайд 16Лежащее в основе строения спирали правило золотого сечения встречается в
природе очень часто в бесподобных по красоте творениях. Самые наглядные
примеры - спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, кактусах, строении лепестков роз и т.д.Слайд 17Священный холм и храм Божественной Афины, Великолепный Парфенон, Похоронив забытые руины, К богам Олимпа
устремлен.
Николай Васютинский
Золотое сечение в архитектуре
Слайд 18Храм
Парфенон
Парфенон имеет 8 колонн по коротким сторонам
и 17 по длинным . Отношение высоты этого здания к
его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.Слайд 21Личность Леонардо да Винчи– одна из загадок истории. Он снискал
славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые
не были осуществлены вплоть до XX в. Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной.Слайд 22Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые
обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями
правильного звездчатого пятиугольника.Хитроумная комбинация двух треугольников построена в соответствии с пропорцией золотого сечения.
Слайд 23Золотое сечение в живописи
Картина или фотография имеет определенные точки, невольно
приковывающие наше внимание, так называемые зрительные центры. Таких точек всего
четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.Слайд 24Картина Шишкина
На этой знаменитой картине И. И.
Шишкина с очевидностью просматриваются мотивы золотого сечения.
Ярко освещенная солнцем
сосна делит длину картины в отношении золотого сечения.Слайд 25Золотое сечение в скульптуре
Скульпторы утверждают, что талия делит совершенное человеческое
тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона
Бельведерского состоит из частей, делящихся по золотым отношениям.Слайд 26Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих
произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая
считалась одним из чудес света) и Афины Парфенос.Слайд 27Шедевром красоты считается
Афродита Милосская,
созданная Агесандром.
Это о ней написал А.Фет
замечательные
строки:
И восхитительно и смело
До чресл сияя наготой
Цветет божественное тело.
Слайд 29Золотое сечение в
других частях тела
Пропорции золотого сечения проявляются и в отношении и других
частей тела - лица, кисти руки, пальцев, всей руки.Слайд 33Что такое «золотое сечение»?.. Что это за идеальное, божественное сочетание?
Может быть, это закон красоты? Или все-таки он — мистическая
тайна? Научный феномен или этический принцип?Анхеля де Куатьэ