Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку геометрии
Содержание
- 1. Презентация к уроку геометрии
- 2. Покоряет вершины тот, кто к ним стремится
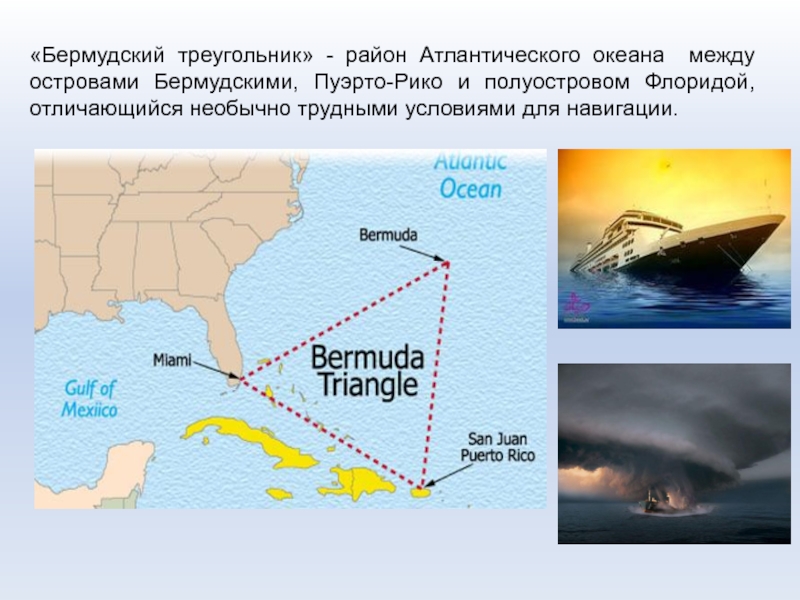
- 3. «Бермудский треугольник» - район Атлантического океана между
- 4. Слайд 4
- 5. Слайд 5
- 6. Треугольник – созвездие Северного полушария.
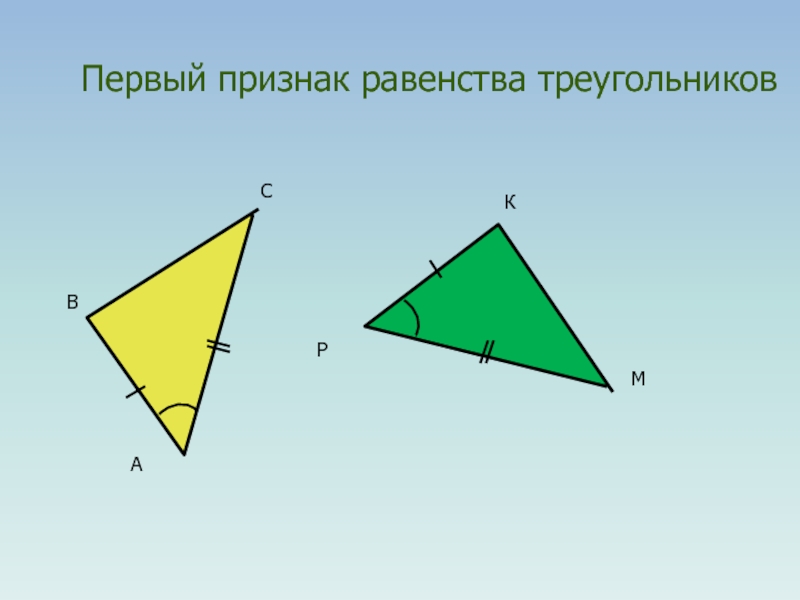
- 7. Первый признак равенства треугольников
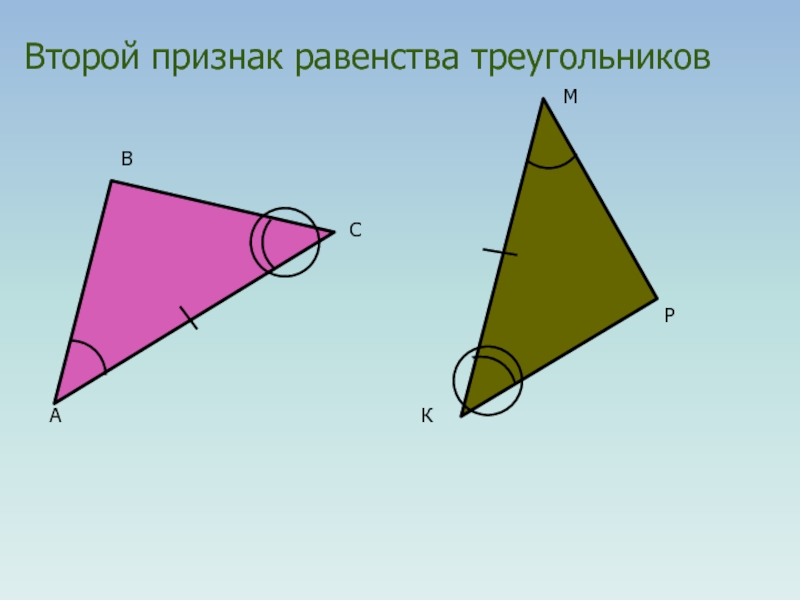
- 8. Второй признак равенства треугольников
- 9. Третий признак равенства треугольников
- 10. ТеоремаКаждая сторона треугольника меньше суммы двух других сторон.
- 11. Дано: ВН = 4см. Найти: АН.
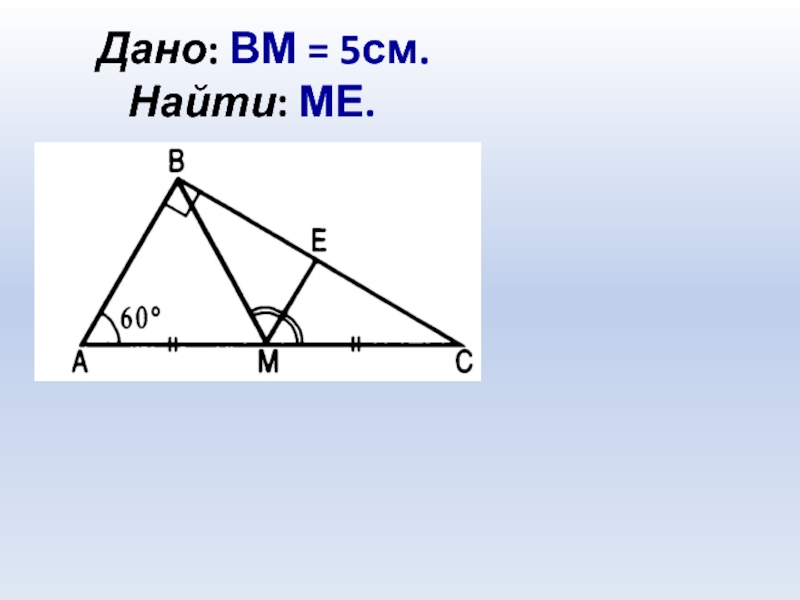
- 12. Дано: ВМ = 5см. Найти: МЕ.
- 13. Сколько треугольников вы увидели? Треугольник – распространенная фигура.
- 14. СОСЧИТАЙ ТРЕУГОЛЬНИКИ
- 15. Если две стороны и угол между ними
- 16. Если сторона и два прилежащих к ней
- 17. Если три стороны одного треугольника соответственно равны
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3«Бермудский треугольник» - район Атлантического океана между островами Бермудскими, Пуэрто-Рико
и полуостровом Флоридой, отличающийся необычно трудными условиями для навигации.
Слайд 15Если две стороны и угол между ними одного треугольника соответственно
равны двум сторонам и углу между ними другого треугольника, то
такие треугольники равныДано: DС= ВF
DCF = СFD
Доказать: DCF = CFB
Доказательство:
1. DС= ВF ( по условию)
DCF = СFD( по услов.)
3. CF – общая
DCF = CFB
по первому признаку
Слайд 16Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники равныДано: NXL = LXK
XLN = XLK
Доказать: XLN = XLK
Доказательство:
NXL = LXK
XLN = XLK
XL – общая
XLN = XLK
по второму признаку
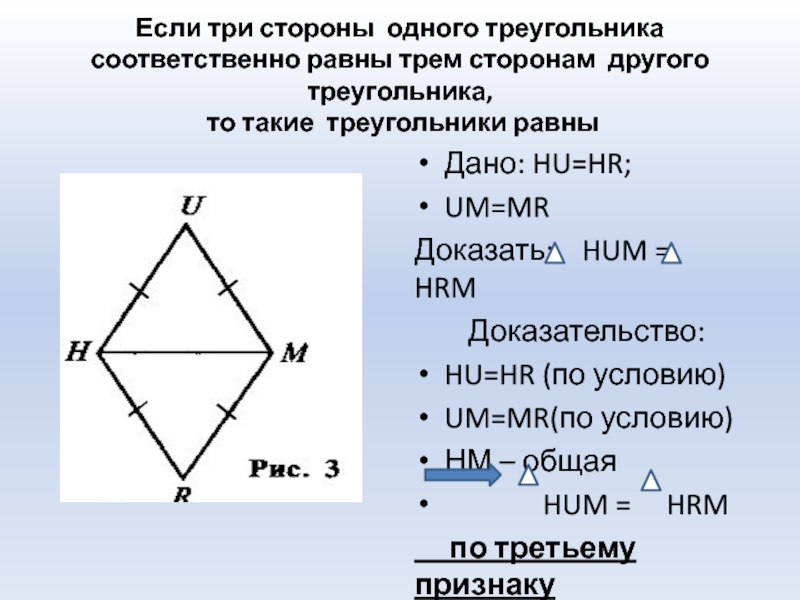
Слайд 17Если три стороны одного треугольника соответственно равны трем сторонам другого
треугольника,
то такие треугольники равны
Дано: HU=HR;
UM=MR
Доказать: HUM =
HRMДоказательство:
HU=HR (по условию)
UM=MR(по условию)
НМ – общая
HUM = HRM
по третьему признаку