Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ньютон и Лейбниц – создатели математического анализа
Содержание
- 1. Ньютон и Лейбниц – создатели математического анализа
- 2. Производная и интегралВ конце 17 века в
- 3. Происхождение производнойРяд задач дифференциального исчисления был решен
- 4. Происхождение производнойНьютон пришел к понятию производной, исходя
- 5. Портрет Ньютона художника Русакова. Мы видим фундаментальной
- 6. Фундаментальный труд Ньютона «Математические начала натуральной философии»(в
- 7. Был летний день. Исаак Ньютон любил размышлять,
- 8. Первые научные опыты Ньютона связаны с исследованиями
- 9. Бином НьютонаБино́м Нью́то́на — формула для разложения
- 10. Долгое время считалось, что для натуральных показателей
- 11. Бином Ньютона в литературеВ художественной
- 12. Происхождение производнойВ подходе Лейбница к
- 13. Происхождение производнойПо мере развития анализа
- 14. Работы Лейбница по математике многочисленны и разнообразны.В
- 15. Кто автор производной?Ньютон создал свой метод, опираясь
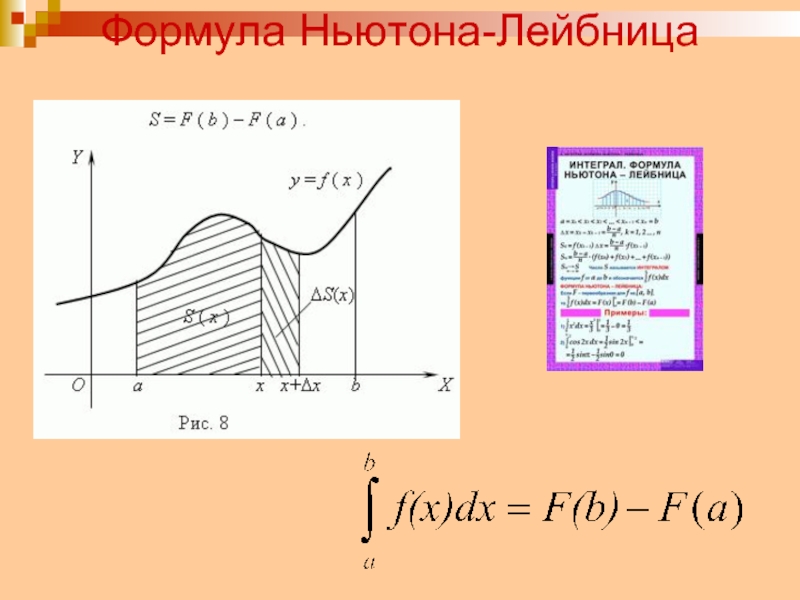
- 16. Формула Ньютона-Лейбница
- 17. Слайд 17
- 18. Памятник Ньютону в Кэмбридже.
- 19. Памятник Лейбницу в Лейпциге.
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Использованные ресурсы:http://ru.wikipedia.org/wiki/Лейбниц,_Готфрид_Вильгельмhttp://www.aphorisme.ru/about-authors/leybnic/?q=3519http://www.fmclass.ru/math.php?id=484121ce1c9d1http://todayinsci.com/L/Leibniz_Gottfried/LeibnizGottfried-Quotations.htmhttp://sat24.ucoz.ru/forum/82-101-2 http://www.dentmaster.ru/node/8060?size=previewhttp://ru.picscdn.com/domain/benisrael.net/http://post.kards.qip.ru/compose/edit/ньютон/9471809/2/njuton_pod_jablonej.htmhttp://www.people.su/32/r1http://www.people.su/32/r1http://lib.rus.ec/b/259787/readhttp://www.help-rus-student.ru/pictures_fail/54/263_2.htmhttp://sokemem.com/review/books-by-isaac-newtonhttp://sokemem.com/review/books-by-isaac-newtonhttp://www.math.spbu.ru/user/jvr/DA_html/_lec_1_04.htmlhttp://www.infanata.com/page/621/http://www.lib.vitebsk.net/libs/11/41/http://chtiva.net/лейбниц/http://www.dhbooks3.ru/c40_nemeckij_yazik?page=113http://bookmix.ru/book.phtml?id=396497http://bookmix.ru/book.phtml?id=396497http://
- 24. Использованные ресурсы:http://www.alib.ru/bs.php4?uid=1129dbb67b5eacfb00831c58dd512a88c759http://www.dom-knigi.ru/book.asp?Art=316871&CatalogID=158http://www.athens.kiev.ua/lejbnic/http://www.100book.ru/predel_funkcij_formuly_nyutona-lejbnica_i_tejlora_b382187.html http://tvsh2004.narod.ru/ma_12-0.htmМордкович А.П. П.В.Алгебра и начала анализа (профильный уровень) 10 класс, М., «Мнемозина», 2006.
- 25. Автор: Заикина Наталья Алексеевна, учитель математики,МОУ «СОШ № 5» г. Саратов
- 26. Скачать презентанцию
Производная и интегралВ конце 17 века в Европе образовались две крупные математические школы. Главой одной из них был Готфрид Вильгельм фон Лейбниц. Его ученики и сотрудники – Лопиталь, братья Бернулли, Эйлер
Слайды и текст этой презентации
Слайд 2Производная и интеграл
В конце 17 века в Европе образовались две
крупные математические школы. Главой одной из них был Готфрид Вильгельм
фон Лейбниц. Его ученики и сотрудники – Лопиталь, братья Бернулли, Эйлер жили и творили на континенте. Вторая школа, возглавляемая Исааком Ньютоном, состояла из английских и шотландских ученых. Обе школы создали новые мощные алгоритмы, приведшие по сути к одним и тем же результатам – к созданию дифференциального и интегрального исчисления.Слайд 3Происхождение производной
Ряд задач дифференциального исчисления был решен еще в древности.
Такие задачи можно найти у Евклида и у Архимеда, однако
основное понятие – понятие производной функции – возникло только в17 веке в связи с необходимостью решить ряд задач из физики, механики и математики, в первую очередь следующих двух: определение скорости прямолинейного неравномерного движения и построения касательной к произвольной плоской кривой.Первую задачу: о связи скорости и пути прямолинейно и неравномерно движущейся точки впервые решил Ньютон
Он пришел к формуле
Слайд 4Происхождение производной
Ньютон пришел к понятию производной, исходя из вопросов механики.
Свои результаты в этой области он изложил в трактате «Метод
флюксий и бесконечных рядов». Написана работа была в 60-е годы 17 века, однако опубликована после смерти Ньютона. Ньютон не заботился о том, чтобы своевременно знакомить математическую общественность со своими работами.Флюксией называлась производная функции – флюэнты.
Флюэнтой таже в дальнейшем называлась первообразная функция.
Слайд 5Портрет Ньютона художника Русакова. Мы видим фундаментальной труд «Математические начала
натуральной философии», в котором Ньютон изложил закон всемирного тяготения и
три закона механики, ставшие основой классической механикиСлайд 6Фундаментальный труд Ньютона «Математические начала натуральной философии»
(в современном переводе «Математические
основы физики»)
был издан в 1686 году в количестве 300 экземпляров.
Распродан за 4 года, что тогда считалось очень быстро.
Слайд 7Был летний день. Исаак Ньютон любил размышлять, сидя в саду,
на открытом воздухе. Предание сообщает, что размышления Ньютона были прерваны
падением налившегося яблока.Так был сформулирован закон всемирного тяготения
Слайд 8Первые научные опыты Ньютона связаны с исследованиями света. В результате
многолетней работы Исаак Ньютон установил, что белый солнечный луч представляет
собой смесь многих цветов.Ньютон построил первый зеркальный телескоп.
Слайд 9Бином Ньютона
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые
целой неотрицательной степени суммы двух переменных, имеющая вид
Слайд 10Долгое время считалось, что для натуральных показателей степени эту формулу,
как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль. Однако
историки науки обнаружили, что формула была известна ещё в Древнем Китае в XIII веке, а также исламским математикам в XV веке.Исаак Ньютон около 1676 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). Из биномиального разложения Ньютон, а позднее и Эйлер, выводили всю теорию бесконечных рядов.
Слайд 11 Бином Ньютона в литературе
В художественной литературе «бином Ньютона»
появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо
сложном.В рассказе А. Конан Дойля «Последнее дело Холмса» Холмс говорит о математике профессоре Мориарти:
«Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая будущность»
Знаменита цитата из «Мастера и Маргариты» М. А. Булгакова: «Подумаешь, бином Ньютона!».
Позже это же выражение упомянуто в фильме «Сталкер» А. А. Тарковского.
Бином Ньютона упоминается:
в повести Льва Толстого «Юность» в эпизоде сдачи вступительных экзаменов в университет Николаем Иртеньевым;
в романе Е.И.Замятина «Мы».
в фильме «Расписание на послезавтра»;
Слайд 12 Происхождение производной
В подходе Лейбница к математическому анализу были
некоторые особенности. Лейбниц мыслил высший анализ не кинематически, как Ньютон,
а алгебраически. Он шел к своему открытию от анализа бесконечно малых величин и теории бесконечных рядов.В 1675 году Лейбниц завершает свой вариант математического анализа, тщательно продумывает его символику и терминологию, отражающую существо дела. Почти все его нововведения укоренились в науке и только термин «интеграл» ввёл Якоб Бернулли (1690), сам Лейбниц вначале называл его просто суммой.
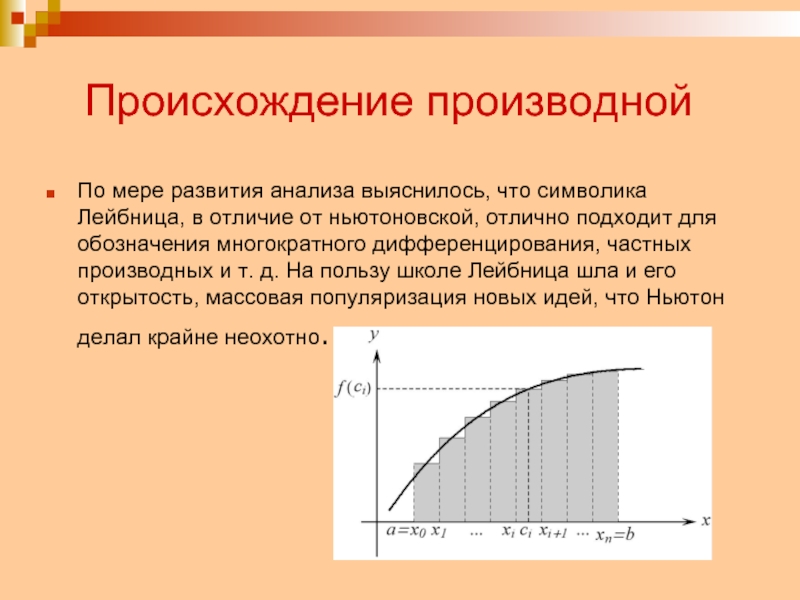
Слайд 13 Происхождение производной
По мере развития анализа выяснилось, что символика
Лейбница, в отличие от ньютоновской, отлично подходит для обозначения многократного
дифференцирования, частных производных и т. д. На пользу школе Лейбница шла и его открытость, массовая популяризация новых идей, что Ньютон делал крайне неохотно.Слайд 14Работы Лейбница по математике многочисленны и разнообразны.
В 1666 года он
написал первое сочинение: «О комбинаторном искусстве». Сейчас комбинаторика и теория
вероятности одна из обязательных тем математики в школе.1672 года Лейбниц изобретает собственную конструкцию арифмометра, гораздо лучше паскалевской — он умел выполнять умножение, деление и извлечение корней. Предложенные им ступенчатый валик и подвижная каретка легли в основу всех последующих арифмометров.
Лейбниц также описал двоичную систему счисления с цифрами 0 и 1, на которой основана современная компьютерная техника.
Слайд 15Кто автор производной?
Ньютон создал свой метод, опираясь на прежние открытия,
сделанные им в области анализа, но в самом главном вопросе
он обратился к помощи геометрии и механики. Когда именно Ньютон открыл свой новый метод, в точности неизвестно. По тесной связи этого способа с теорией тяготения следует думать. что он был выработан Ньютоном между 1666 и 1669 годами.Лейбниц обнародовав главные результаты своего открытия в 1684, опережая Исаака Ньютона, который еще раньше Лейбница пришел к сходным результатам, но не публиковал их.
Впоследствии на эту тему возник многолетний спор о приоритете открытия дифференциального исчисления.
Слайд 23Использованные ресурсы:
http://ru.wikipedia.org/wiki/Лейбниц,_Готфрид_Вильгельм
http://www.aphorisme.ru/about-authors/leybnic/?q=3519
http://www.fmclass.ru/math.php?id=484121ce1c9d1
http://todayinsci.com/L/Leibniz_Gottfried/LeibnizGottfried-Quotations.htm
http://sat24.ucoz.ru/forum/82-101-2
http://www.dentmaster.ru/node/8060?size=preview
http://ru.picscdn.com/domain/benisrael.net/
http://post.kards.qip.ru/compose/edit/ньютон/9471809/2/njuton_pod_jablonej.htm
http://www.people.su/32/r1http://www.people.su/32/r1http://lib.rus.ec/b/259787/read
http://www.help-rus-student.ru/pictures_fail/54/263_2.htm
http://sokemem.com/review/books-by-isaac-newtonhttp://sokemem.com/review/books-by-isaac-newtonhttp://www.math.spbu.ru/user/jvr/DA_html/_lec_1_04.html
http://www.infanata.com/page/621/
http://www.lib.vitebsk.net/libs/11/41/
http://chtiva.net/лейбниц/
http://www.dhbooks3.ru/c40_nemeckij_yazik?page=113
http://bookmix.ru/book.phtml?id=396497http://bookmix.ru/book.phtml?id=396497http://
Слайд 24Использованные ресурсы:
http://www.alib.ru/bs.php4?uid=1129dbb67b5eacfb00831c58dd512a88c759
http://www.dom-knigi.ru/book.asp?Art=316871&CatalogID=158
http://www.athens.kiev.ua/lejbnic/
http://www.100book.ru/predel_funkcij_formuly_nyutona-lejbnica_i_tejlora_b382187.html
http://tvsh2004.narod.ru/ma_12-0.htm
Мордкович А.П. П.В.Алгебра и начала анализа (профильный уровень)
10 класс, М., «Мнемозина», 2006.
Теги