Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Готовимся к ЕГЭ. Несколько типов "задач на работу"
Содержание
- 1. Готовимся к ЕГЭ. Несколько типов "задач на работу"
- 2. Задачи на работу делятся на два типа:задачи, в
- 3. Раздельная работаПервая труба пропускает на 3л воды
- 4. В задачах мы имеем дело с тремя параметрами:пропускная
- 5. Эти параметры связаны таким соотношением: A(работа)=A/t(производительность)*t(время)
- 6. В задаче спрашивается, сколько литров
- 7. Теперь заполним столбец, параметры которого даны. Это объем резервуара:
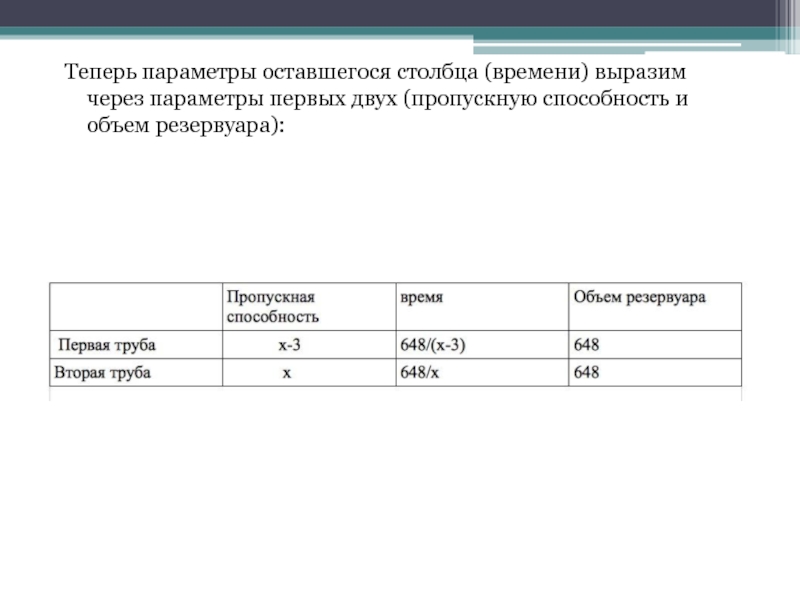
- 8. Теперь параметры оставшегося столбца (времени) выразим через параметры первых двух (пропускную способность и объем резервуара):
- 9. Составим уравнение:
- 10. Приравняем числитель к нулю, раскроем скобки и
- 11. Задача на совместную работу. Если в задаче
- 12. Объем работы, если он не указан отдельно, принимаем
- 13. Даша и Маша пропалывают грядку за 12
- 14. Решим уравнение:
- 15. Классическая задача на совместную работу: Первая труба
- 16. У нас 2 неизвестных, поэтому будем составлять систему
- 17. Получили систему уравнений:
- 18. -4 – не подходит по смыслу. Ответ: 6
- 19. Скачать презентанцию
Задачи на работу делятся на два типа:задачи, в которых выполняется раздельная работа – эти задачи решаются аналогично задачам на движение.задачи на совместную работу.
Слайды и текст этой презентации
Слайд 1Готовимся к ЕГЭ
Несколько типов «задач на работу»
Подготовила
Учитель математики первой категориии
Гимназии
№96
Слайд 2Задачи на работу делятся на два типа:
задачи, в которых выполняется раздельная работа –
эти задачи решаются аналогично задачам на движение.
задачи на совместную работу.
Слайд 3Раздельная работа
Первая труба пропускает на 3л воды в минуту меньше,
чем вторая. Сколько литров воды в минуту пропускает вторая труба,
если резервуар объемом 648 л она заполняет на 3 мин. быстрее, чем первая труба?
Слайд 4В задачах мы имеем дело с тремя параметрами:
пропускная способность трубы(А/t) –
объем жидкости, который труба пропускает в единицу времени (л/мин);
объем резервуара(A),
который необходимо заполнить, или, наоборот, освободить (л);Время(t) (мин)
Слайд 6 В задаче спрашивается, сколько литров воды в минуту
пропускает вторая труба – эту величину мы и примем за
. Поскольку по условию задачи первая труба пропускает на 3л воды в минуту меньше, чем вторая, то пропускную способность первой трубы обозначим .
Слайд 8Теперь параметры оставшегося столбца (времени) выразим через параметры первых двух
(пропускную способность и объем резервуара):
Слайд 10Приравняем числитель к нулю, раскроем скобки и приведем подобные члены.
Получим уравнение:
-24 - не подходит по смыслу задачи.
Ответ: 27 л/мин.
Слайд 11Задача на совместную работу.
Если в задаче встречаются слова «выполнили работу
вместе» или слова «совместная работа», значит это задача на совместную работу.
Слайд 12Объем работы, если он не указан отдельно, принимаем равным 1.
Вводим
два неизвестных:
х – время выполнения всей работы кем-то (или чем-то) первым
y
- время выполнения всей работы кем-то (или чем-то) вторым.(В некоторых задачах «выгоднее» принять за неизвестные производительность)
Тогда
1/x – производительность кого-то (или чего-то) первого
1/y - производительность кого-то (или чего-то) второго
И в этом месте появляется параметр, которого не было в задачах на раздельную работу, а именно – совместная производительность
совместная производительность равна:
1/x+1/y
Слайд 13Даша и Маша пропалывают грядку за 12 минут, а одна
Маша — за 20 минут. За сколько минут пропалывает грядку одна
Даша?Объем работы = производительность * время.
Про Машу нам все известно: время ее работы равно 20, следовательно, ее производительность равна 1/20.
Пусть Даша пропалывает грядку за х минут, тогда ее производительность равна 1/x.
Тогда совместная производительность равна:
1/20+1/x
Объем работы примем равным 1.
Слайд 15Классическая задача на совместную работу:
Первая труба наполняет резервуар на
6 минут дольше, чем вторая. Обе трубы наполняют этот же
резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Слайд 16У нас 2 неизвестных, поэтому будем составлять систему из двух уравнений.
По
условию задачи, первая труба наполняет резервуар на 6 минут дольше, чем
вторая, следовательно время работы первой трубы на 6 минут больше, чем второй:1) x=y+6
Обе трубы наполняют этот же резервуар за 4 минуты, следовательно, время совместной работы равно 4 минуты. Получаем второе уравнение системы:
2) (1/x + 1/y)*4=1
