"Усеченная пирамида"

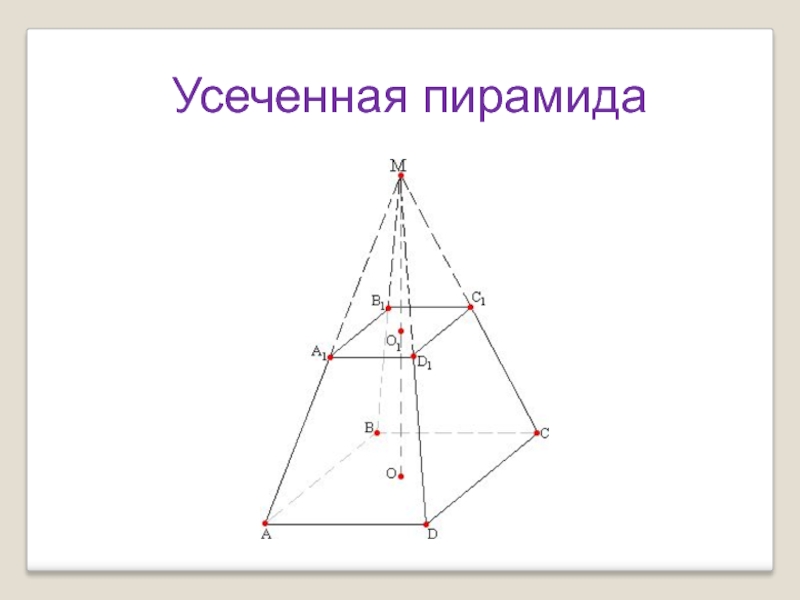
пирамиды, заключенная между ее основанием и секущей плоскостью, параллельной

Плоскость параллельная основанию пирамиды, разбивает её на два многогранника. Один из них является пирамидой, а другой называется усеченной пирамидой.

в параллельных плоскостях , и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn,

A1A2…An и B1B2…Bn – это нижнее и верхнее основания.

A1A2B2B1, A2A3B3B2,…, AnA1B1Bn – это боковые грани пирамиды.

А1В1, А2В2,…, AnBn – это боковые ребра усеченной пирамиды.

верхнего основания к нижнему основанию – называется высотой усеченной пирамиды.
А1
К
К1

сечением правильной пирамиды плоскостью, параллельной основанию
Основания правильной усеченной

и все углы равны.





Центр окружности, описанной около правильного многоугольника

называется сумма площадей основания и всех боковых граней.

Sполн =Sбок+Sосн

Площадью боковой поверхности (Sбок) пирамиды называется сумма площадей её боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

периметров оснований на апофему.
α1
h
Найдем площадь одной

Т.к. эта усечённая пирамида правильная, то