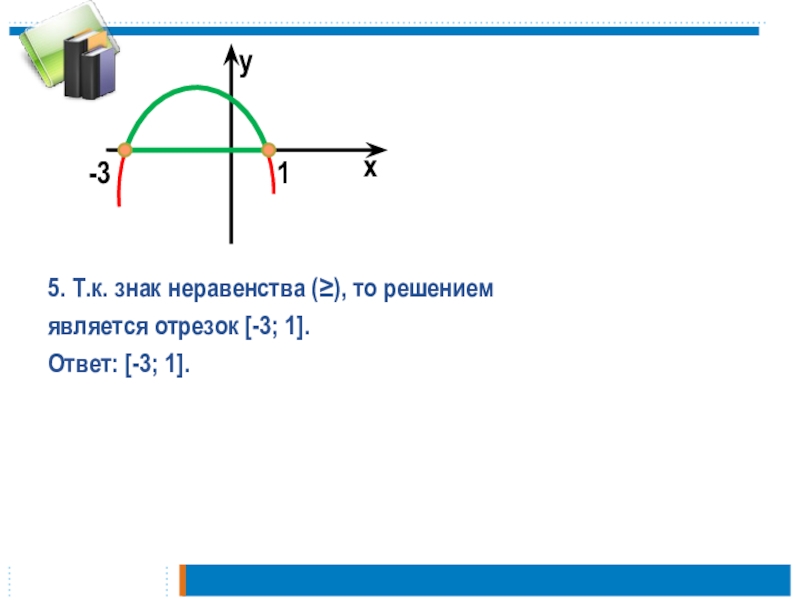
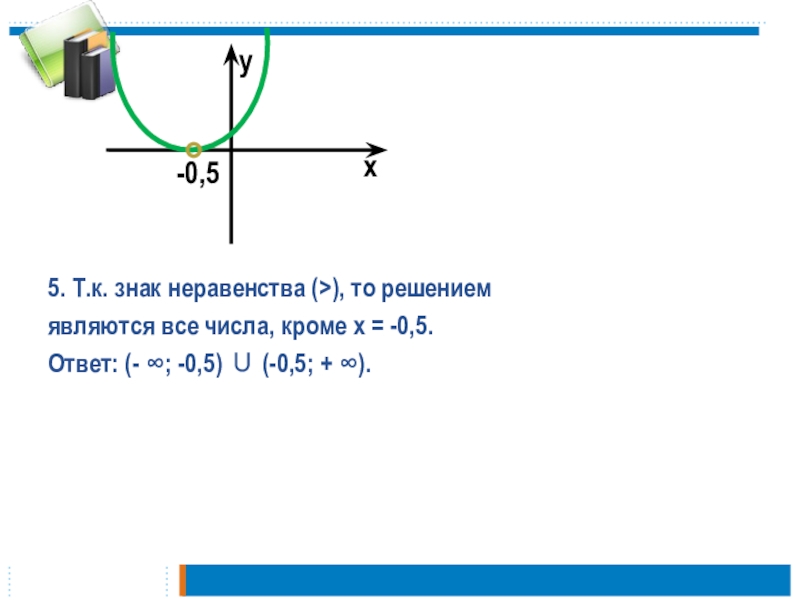
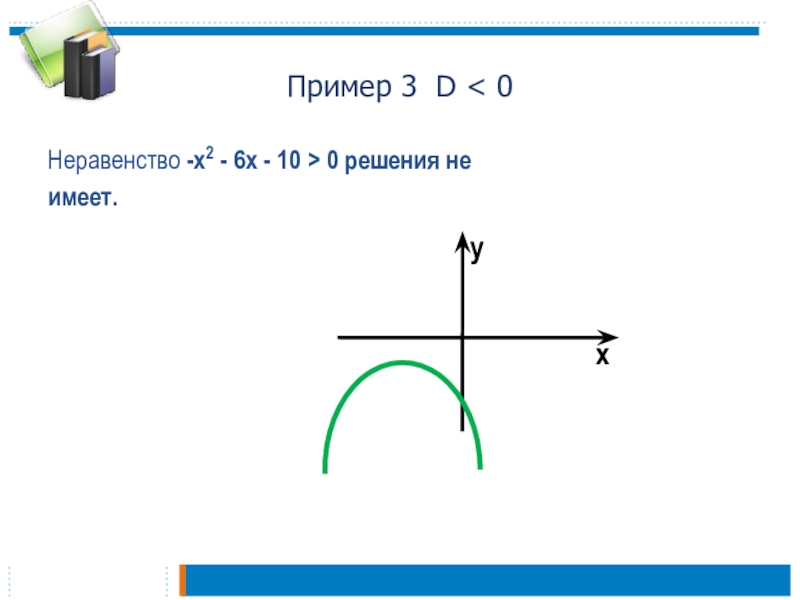
ах2 + bx + с.
2. Определяем направление ветвей параболы у
= ах2 + bx + с(при а0 ветви направлены вверх; при а0 ветви направлены вниз).
3. Находим нули функции, т.е. решаем уравнение ах2+bx+с=о.