Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сложные тела вращения (презентация к уроку по геометрии,11 класс).
Содержание
- 1. Сложные тела вращения (презентация к уроку по геометрии,11 класс).
- 2. Сфероид – Эллипсоид вращенияэто фигура вращенияэто фигура вращения в трёхмерном пространствеэто фигура
- 3. Форма Земли — в хорошем приближении представляет собой сплюснутый
- 4. Гиперболоид вращения - (От греческого - гиперб
- 5. ПрименениеВ науке и техникеСвойство двуполостного гиперболоида вращения
- 6. Сечения однополостного гиперболоида двумя плоскостямиИзображение однополостного гиперболоида
- 7. Эллиптический параболоидпредставляет собой поверхность вращения, образованную вращением параболы
- 8. Гиперболический параболоид Поверхность образована движением параболы, ветви
- 9. Параболоиды в мире В техникеЧасто используется свойство
- 10. Псевдосфера Поверхность Поверхность постоянной отрицательной кривизны Поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты.Трактриса
- 11. Катеноид Поверхность, образуемая вращением цепной линииЦепная линияФорму катеноида
- 12. Тор Тело вращенияТело вращения, получаемое вращением образующей окружности вокруг
- 13. Сечения тора
- 14. Шаровой сектор Геометрическое тело, возникающее при вращении сектораГеометрическое
- 15. Шаровой сегментШаровым сегментом называется часть шара, которую отрезает
- 16. Шаровой слойчасть шара, которая содержится между двумя
- 17. Спасибо за внимание!
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Презентация по геометрии
Учитель математики
МКОУ СОШ № 6
Гаспарян Ирина Вазгеновна.
Сложные тела
вращения
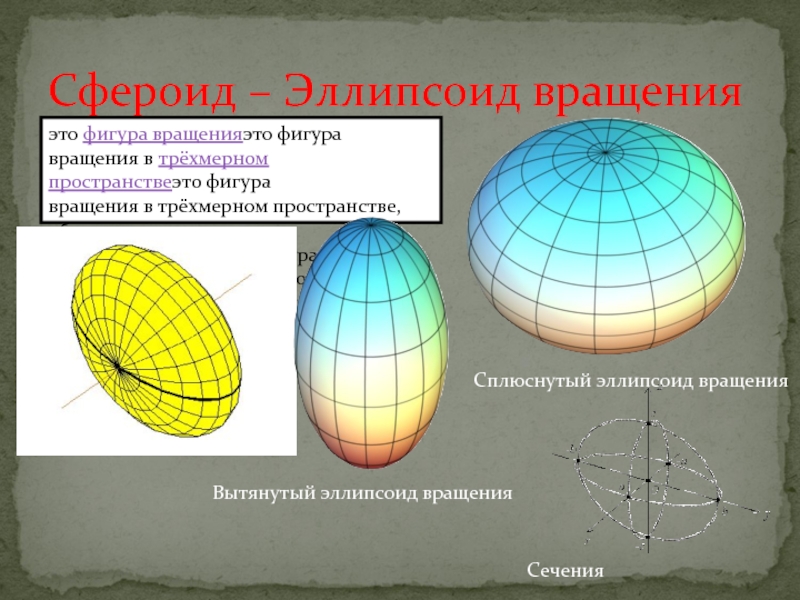
Слайд 2Сфероид – Эллипсоид вращения
это фигура вращенияэто фигура вращения в трёхмерном пространствеэто фигура вращения в трёхмерном пространстве, образованная
при вращении эллипсаэто фигура вращения в трёхмерном пространстве, образованная при вращении эллипса вокруг одной из
его главных осей.Сплюснутый эллипсоид вращения
Вытянутый эллипсоид вращения
Сечения
Слайд 3Форма Земли — в хорошем приближении представляет собой сплюснутый эллипсоид вращения
Свойство вытянутого
эллипсоида вращения отражать лучи, направленные в один из фокусов, в
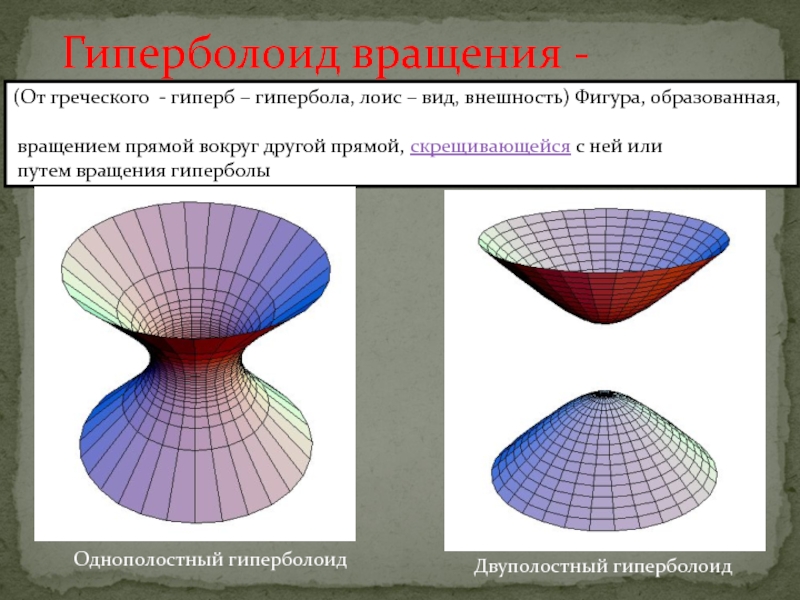
другой фокус, используется в телескопах системы ГрегориСвойство вытянутого эллипсоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Грегори и в антеннах Грегори.Слайд 4Гиперболоид вращения -
(От греческого - гиперб – гипербола, лоис
– вид, внешность) Фигура, образованная,
вращением прямой вокруг другой прямой, скрещивающейся с
ней илипутем вращения гиперболы
Однополостный гиперболоид
Двуполостный гиперболоид
Слайд 5Применение
В науке и технике
Свойство двуполостного гиперболоида вращения отражать лучи, направленные
в один из фокусов, в другой фокус, используется в телескопах системы
Кассегрена ив антеннах Кассегрена.
В архитектуре
Слайд 6Сечения однополостного гиперболоида двумя плоскостями
Изображение однополостного гиперболоида с помощью сечений
Сечения
двуполостного гиперболоида
плоскостью
Изображение двуполостного гиперболоида с помощью сечений
Слайд 7Эллиптический параболоид
представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси,
проходящей через вершину данной параболы.
сечения эллиптического параболоида координатными плоскостями
дополнительные сечения
параболоидаСлайд 8Гиперболический параболоид
Поверхность образована движением параболы, ветви которой направлены вниз, по
параболе, ветви которой направлены вверх, при условии, что первая парабола
соприкасается со второйсвоей вершиной.
Изображение гиперболического параболоида с помощью сечений
Дополнительное сечение
Слайд 9Параболоиды в мире
В технике
Часто используется свойство параболоида вращения собирать пучок
лучей, параллельный главной оси, в одну точку — фокусЧасто используется свойство параболоида
вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основаны параболические антенныЧасто используется свойство параболоида вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основаны параболические антенны, телескопы-рефлекторыЧасто используется свойство параболоида вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основаны параболические антенны, телескопы-рефлекторы, прожекторыЧасто используется свойство параболоида вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основаны параболические антенны, телескопы-рефлекторы, прожекторы, автомобильные фары и т. д.В литературе
Устройство, описанное в романе А. Н. Толстого «Гиперболоид инженера Гарина», на самом
деле параболоид.
Слайд 10Псевдосфера
Поверхность Поверхность постоянной отрицательной кривизны Поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около
её асимптоты.
Трактриса
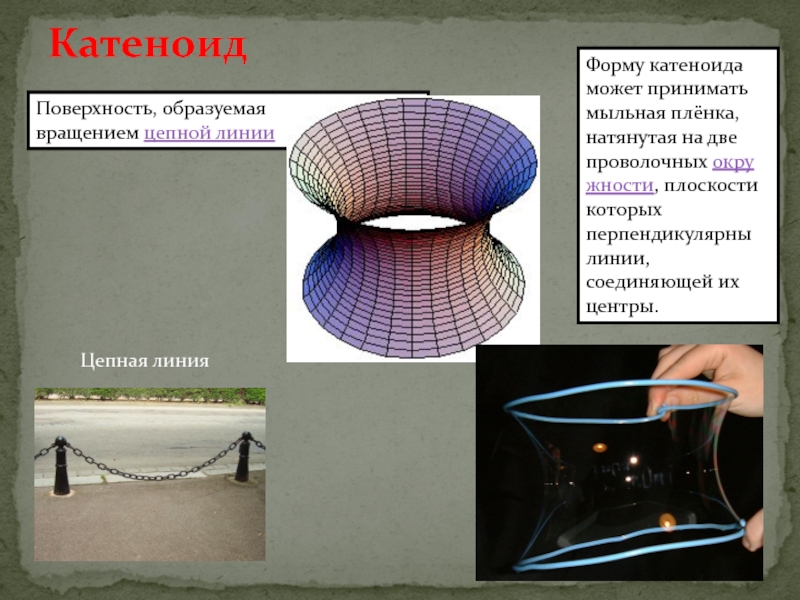
Слайд 11Катеноид
Поверхность, образуемая вращением цепной линии
Цепная линия
Форму катеноида может принимать мыльная плёнка,
натянутая на две проволочных окружности, плоскости которых перпендикулярны линии, соединяющей их
центры.
Слайд 12Тор
Тело вращенияТело вращения, получаемое вращением образующей окружности вокруг оси, лежащей в плоскости
этой окружности.
Красным - образующая окружность
Тор трансформируется в шар
При сечении тора «диагональной»
касательной плоскостью, проходящей через центр тора (эта плоскость автоматически получается бикасательной) образуются окружности Вилларсо.