Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Способы решения систем уравнений"
Содержание
- 1. "Способы решения систем уравнений"
- 2. ЦельРассмотреть различные способы решения систем уравнений
- 3. Из истории решения системы уравнений
- 4. Из истории решения системы уравнений Диофант,
- 5. Различные способы решения систем уравнений метод подстановкиметод сложенияметод введения новых переменныхграфический метод
- 6. Метод подстановки Одно из уравнений системы
- 7. Метод сложенияПреобразовать коэффициенты так, чтобы
- 8. Метод введения новых переменныхЗамени одно
- 9. Графический методВыразить в обоих уравнениях системы переменную
- 10. Способ подстановкиРешить систему уравнений:Решение:xy = -3;
- 11. Если z
- 12. Метод сложения Решить систему уравнений: Умножу первое
- 13. Преимущества и недостатки метода
- 14. Метод введения новых переменных Пусть
- 15. Графический способ Графиком уравнения
- 16. Графики пересекаются в четырех точках
- 17. Графический метод решения систем,
- 18. Проверь себяРеши систему уравнений, используя метод подстановки:Реши
- 19. Мы
- 20. Информационные источникиhttphttp://http://festivalhttp://festival.1http://festival.1septemberhttp://festival.1september.http://festival.1september.ruhttp://festival.1september.ru/http://festival.1september.ru/articleshttp://festival.1september.ru/articles/515367/http://revolution.allbest.ru/mathematics/00029395_0.htmlhttp://www.schoolife.ru/education/algebra/eqs-ineqs/sistemy-yravnenii.html
- 21. Скачать презентанцию
ЦельРассмотреть различные способы решения систем уравнений
Слайды и текст этой презентации
Слайд 1 Способы решения систем уравнений
Автор:
Кудряшова Любовь Александровна, учитель математики.
2010 г
Слайд 3Из истории решения системы уравнений
В
древневавилонских текстах, написанных в III—II тысячелетиях до н. э.,
содержится немало задач, решаемых с помощью составления систем уравнений. Например: «Площади двух своих квадратов я сложил: Сторона второго квадрата равна стороны первогои еще 5».
Соответствующая система уравнений в современной записи имеет вид:
Хотя вавилоняне и не имели алгебраической
символики, они решали задачи алгебраическим
методом.
Слайд 4Из истории решения системы уравнений
Диофант, который не
имел обозначений для многих неизвестных, прилагал немало усилий для
выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения.Задача 21.
«Найти два числа, зная, что их сумма равна 20, а сумма их квадратов — 208»
Слайд 5Различные способы решения систем уравнений
метод подстановки
метод сложения
метод введения новых
переменных
графический метод
Слайд 6Метод подстановки
Одно из уравнений системы преобразуют к виду, в
котором y выражено через х
( или х через y )Полученное выражение подставляют вместо y (или вместо х ) во второе уравнение. В результате получается уравнение с одной переменной
Находят корни этого уравнения
Воспользовавшись выражением y через х(или х через y), находят соответствующие значения х (или y)
Слайд 7
Метод сложения
Преобразовать коэффициенты так, чтобы коэффициенты при
х или у были противоположными числами
Сложить получившиеся уравнения
Решить уравнение
с одной переменной
Слайд 8 Метод введения новых переменных
Замени одно или два выражения
в уравнениях системы новыми переменными так, чтобы вновь полученные уравнения
стали более простыми.Реши полученную систему уравнений методам наиболее подходящим для э той системы уравнений.
Сделай обратную замену, для того, чтобы найти значения первоначальных переменных.
Запиши ответ в виде пар значений (x,y), которые были найдены на третьем шаге.
Слайд 9Графический метод
Выразить в обоих уравнениях системы переменную у
через переменную х
Построить графики функций в одной
системе координат.
Отметить точки
пересечения графиков, выписать их координаты.Записать в ответ полученные пары
чисел (х;у).
Слайд 11
Если z =9, то
,
z =1, то-3,-1,1,3 отличны от нуля, значит, они являются корнями уравнения:
Ответ: (3;-1), (-3;1), (-1;3), (1;-3)
Слайд 12Метод сложения
Решить систему уравнений:
Умножу первое уравнение системы на число
2,
а второе на число -3, получу
Сложу уравнение системы:
Решу уравнение:
Подставлю
найденное число вместо n в первое уравнение исходной системы:Решу уравнение относительно m:
Система имеет одно решение: (-0,5;1)
Ответ: (-0,5;1)
Слайд 13Преимущества и недостатки метода
Преимущества:
Систему уравнений
легче решать методом сложения, когда
коэффициенты при X и Y сразу являются противоположными числами.Метод позволяет быстро исключить одну из неизвестных переменных и найти другую.
Недостатки:
Метод сложения невозможно применить,когда у переменных в двух уравнениях разные
показатели степени.
Слайд 14 Метод введения новых переменных
Пусть
и
учитывая, что
получим:
Если u=-3, то
или
Тогда получим:
и
Полученные системы тоже являются симметричными системами, которые уже решали.
Итак, (3;1), (-1;3), (-3;1),(1;-3) - решения данной системы.
Слайд 15Графический способ
Графиком уравнения
является окружность с
центром в точке (0;0) и радиусом
В одной системе координат построим графики уравнений: ху= -3 и
Графиком уравнения ху=-3 является гипербола, ветви которой расположены во II и IV координатных четвертях.
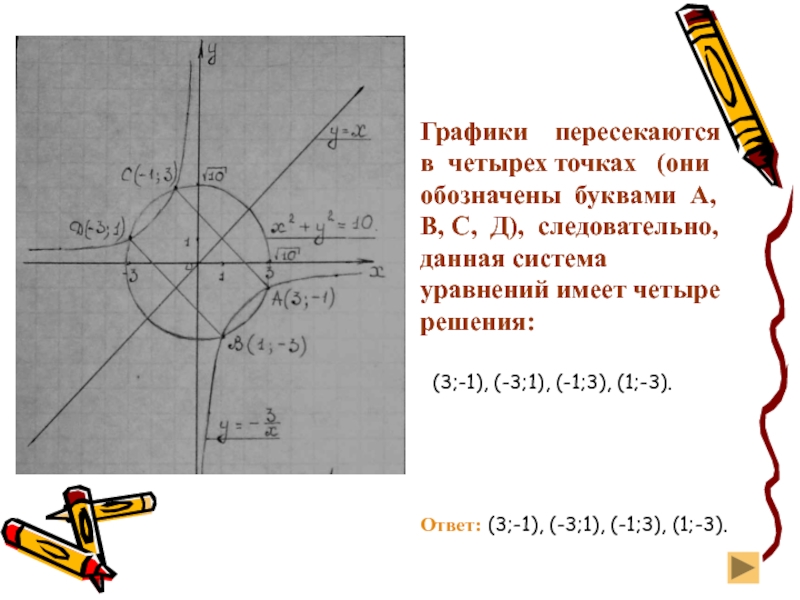
Слайд 16Графики пересекаются в четырех точках (они обозначены буквами
А, В, С, Д), следовательно, данная система уравнений имеет четыре
решения:(3;-1), (-3;1), (-1;3), (1;-3).
Ответ: (3;-1), (-3;1), (-1;3), (1;-3).
Слайд 17
Графический метод решения систем, как и
графический метод решения уравнений, красив, но ненадежен:
во-первых, потому, что графики
уравнений мы сумеем построить далеко не всегда;во-вторых, даже если графики уравнений удалось построить, точки пересечения могут быть не такими «хорошими», как в специально подобранных примерах учебника, а то и вовсе могут оказаться за пределами чертежа.
Преимущества и недостатки метода
Слайд 18Проверь себя
Реши систему уравнений, используя метод подстановки:
Реши систему уравнений, используя
метод сложения:
Реши систему уравнений , используя
графический способ:Реши систему уравнений, используя метод подстановки:
Слайд 19 Мы рассмотрели четыре
различных способов решения систем уравнений. Каждый выберет
для себя способ, который ему больше всего понравился, самое главное - что каждый из Вас научился решать системы такого вида и поэтому эпиграфом могли служить слова Б.В.Гнеденко:Вывод
«Ничто так не содействует усвоению предмета, как действие с ним в разных ситуациях»
Слайд 20Информационные источники
httphttp://http://festivalhttp://festival.1http://festival.1septemberhttp://festival.1september.http://festival.1september.ruhttp://festival.1september.ru/http://festival.1september.ru/articleshttp://festival.1september.ru/articles/515367/
http://revolution.allbest.ru/mathematics/00029395_0.html
http://www.schoolife.ru/education/algebra/eqs-ineqs/sistemy-yravnenii.html
