Комбинаторика 5 класс

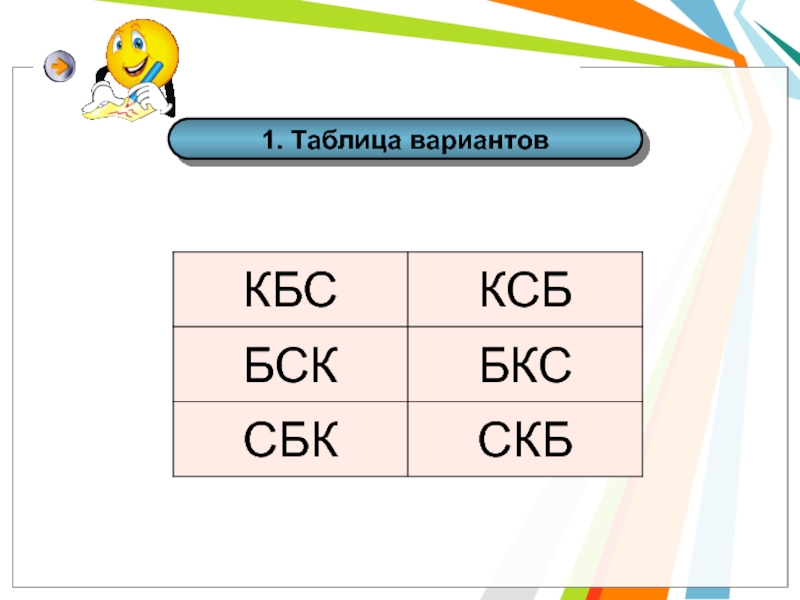
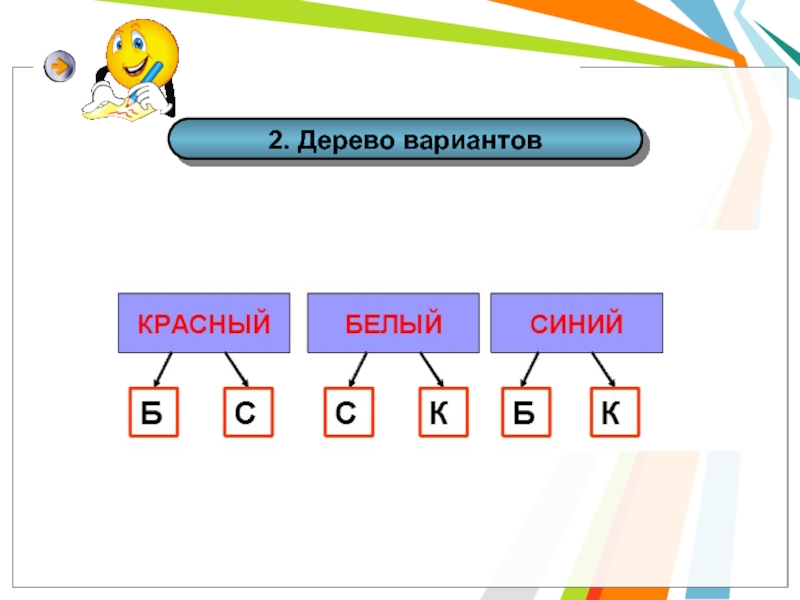
to add Text
Click to add Text
Click to add

Text
Click to add Text
Click to add Text

Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься.

«Витязь на распутье» 1882 г. Васнецов Виктор Михайлович

«комбинаторика» происходит от латинского слова «combina», что в переводе на

русский означает – «сочетать», «соединять».
Комбинаторика - раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями.

предметы в определенном порядке, отыскивать среди разных расположений наилучшее –

вот задачи, решаемые в быту, на охоте или в сражениях.

Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э.

в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые

можно составить из частей особым образом, разрезанного квадрата, и т.д.

шахматы и т. д.).
В каждой из этих игр приходилось рассматривать

различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных.

несет 7 мешков, в каждом мешке лежит 7 хлебов, у

каждого хлеба лежит 7 ножей, каждый нож нарежет 7 кусков хлеба. Чему равно общее число всего перечисленного?
В историческом отношении эта задача интересна тем, что она тождественна с задачей о кошках, которая встречалась в папирусе Ринда (Египет), то есть через три тысячи лет после египетских школьников задачу предлагалось решить итальянским школьникам.

Задача о семи старухах

на различных перестановках букв, чисел, заменах букв с использованием ключевых

слов и т. д.

стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об

искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика».

рукава перекинуто 7 мостов. Спрашивается, можно ли пройти все 7

мостов так, чтобы каждый был пройден по одному лишь разу.
Эйлер показал, что это невозможно, и рассмотрел более общую задачу, в которой речь идет о любом числе местностей, как-либо разделенных рукавами рек и соединенных мостами.

- 1 способ
3 ∙ 2 ∙ 1 = 6
Ответ: 6

способов

3. Правило умножения

цифры:

а) 1 и 2;

б) 3 и 0?



Задача

1

2 и 3, если:



а) цифры в записи числа не

повторяются;


б) цифры в записи числа могут повторяться?

0, если:


а) цифры в записи числа не повторяются;

б)

цифры в записи числа могут повторяться?

Задача 3

различными способами они могут сесть рядом?