Слайд 2Цели и задачи урока:
познакомить учащихся с телами вращения;
формирование представлений о
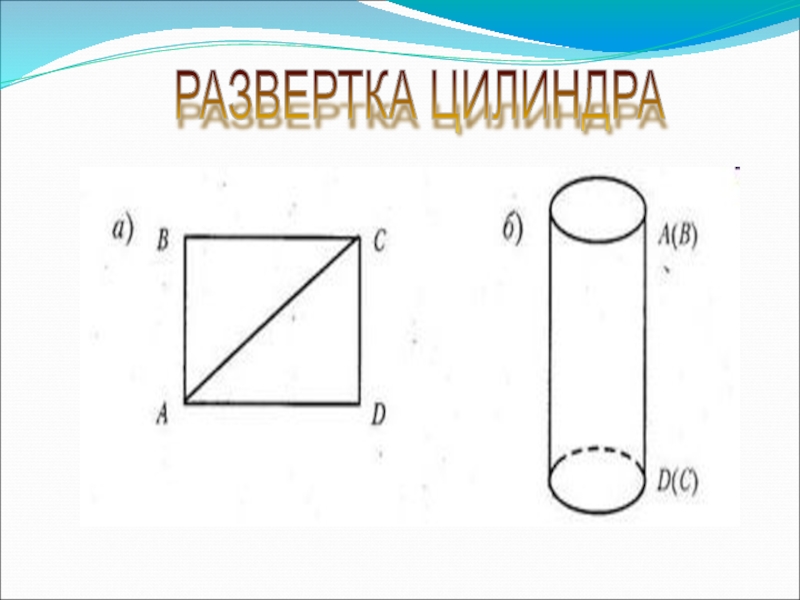
цилиндрической поверхности;
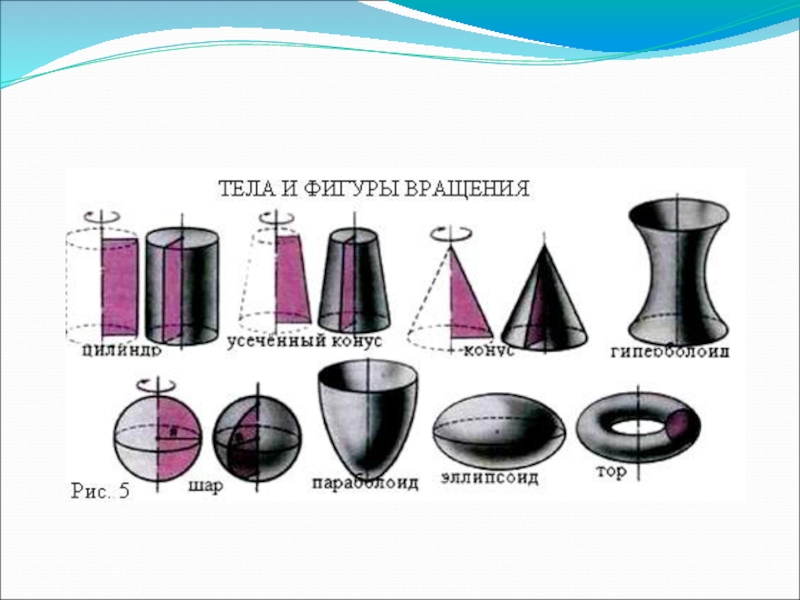
формирование представлений о цилиндре и его видах;
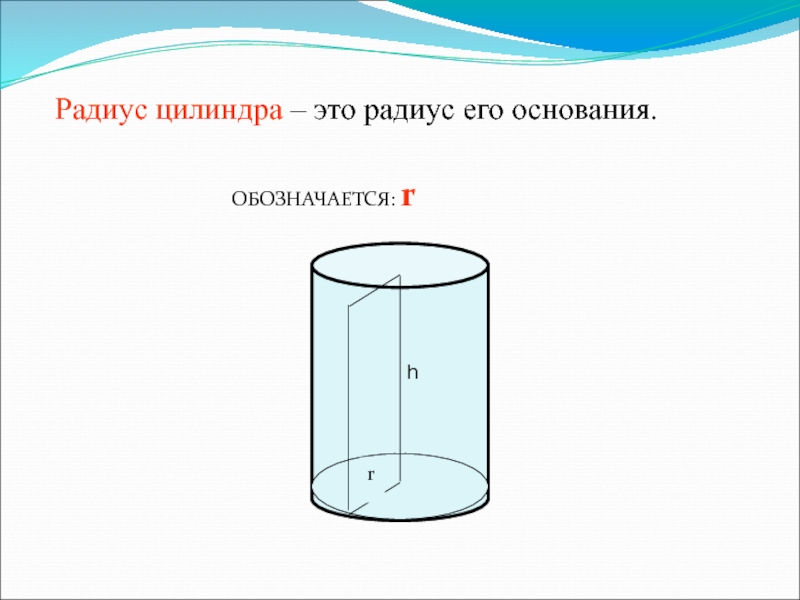
формирование представлений о
составляющих цилиндра;
отработка представлений о цилиндре;
развивать пространственное воображение и логическое мышление;
воспитывать аккуратность при выполнении чертежей.
Слайд 3ПЛАН УРОКА
Устная работа.
Изучение нового материала.
Закрепление, решение задач.
Итог урока.
Задание на дом.
Слайд 5Общее название этих тел связано с тем, что их образование
можно связать с вращением некоторой плоской фигуры вокруг ее стороны
как оси.
Слайд 7
Цилиндр – это тело, полученное вращением прямоугольника вокруг прямой, содержащей
его сторону.
Слайд 8Элементы цилиндра
О
ОСЬ ЦИЛИНДРА
ОСНОВАНИЕ ЦИЛИНДРА
ОБРАЗУЮЩАЯ
РАДИУС
ВЫСОТА ЦИЛИНДРА
Слайд 9
Прямая, вокруг которой вращается прямоугольник называется осью цилиндра
Образующая цилиндра –
это отрезок, соединяющий соответствующие точки окружностей кругов.
ОБОЗНАЧАЕТСЯ: l
У цилиндра множество
образующих.
Высота цилиндра – это расстояние между плоскостями его оснований, т.е. отрезок оси между центрами его оснований.
ОБОЗНАЧАЕТСЯ: H
Длина высоты прямого цилиндра равна длине образующей
Слайд 10Радиус цилиндра – это радиус его основания.
ОБОЗНАЧАЕТСЯ: r
Слайд 12Если секущая плоскость
проходит через ось
цилиндра, то сечение
является прямоугольником.
Такое
сечение носит название осевого сечения.
Слайд 13
Если секущая плоскость
перпендикулярна к оси
цилиндра, то сечение
является кругом.
Слайд 17
Осевое сечение цилиндра – квадрат, диагональ которого равна 20см.
Найти высоту цилиндра, площадь основания, площадь боковой поверхности.
Решение: АА1В1В –
квадрат. АВ=ВВ1
АВ1=20см. АВ12=АВ2+ВВ12
Ответ:
(см2).
ЗАДАЧА 1
Слайд 18Решение задач
Решить задачи №521, 523, 525,
При решении задачи 521
использовать свойства 10 и 20 параллельных плоскостей, определения цилиндра и
прямоугольника, теорема Пифагора.
В задаче 523 применять теорему Пифагора и формулу площади круга.
При решении задачи 525 можно использовать алгебраический способ – составление системы уравнений по условию задачи (применение формулы площади прямоугольника и круга).
Слайд 19Домашнее задание:
п.53, 54. №522,524,526, 538
