Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Центральная симметрия 8 класс
Содержание
- 1. Центральная симметрия 8 класс
- 2. Центральная симметрия. Определение:
- 3. Приведём примеры фигур, обладающие центральной симметрией:
- 4. АВОДве точки А и В называются симметричными
- 5. Например: На рисунке точки М и
- 6. Центральная симметрия в
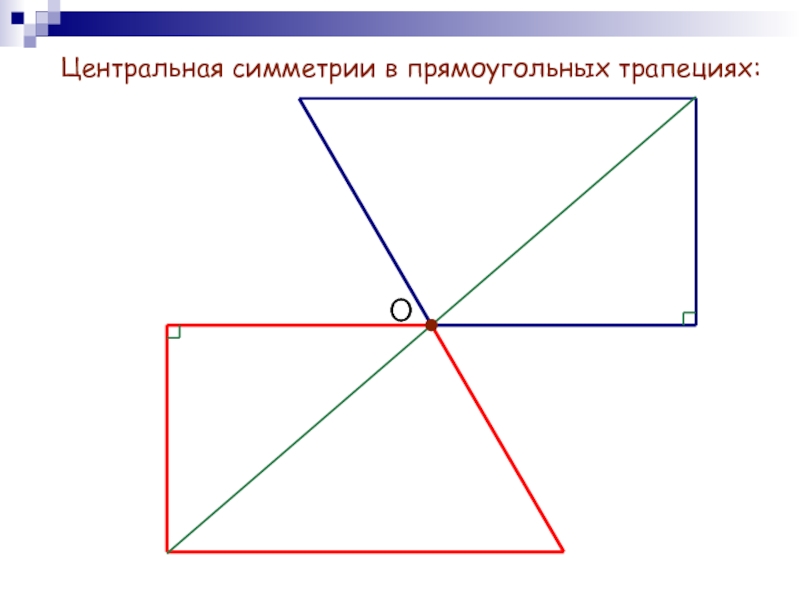
- 7. Центральная симметрии в прямоугольных трапециях:О
- 8. Центральная симметрия в квадратах:О
- 9. Центральная симметрия в параллелограммах:О
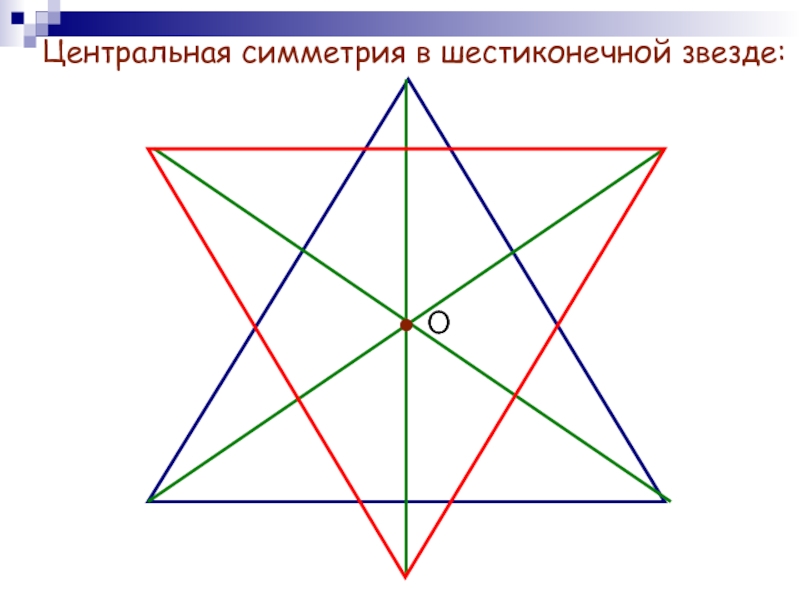
- 10. Центральная симметрия в шестиконечной звезде:О
- 11. Точка О является центром симметрии, если при
- 12. Прямая также обладает центральной симметрией,
- 13. Применение на практике:
- 14. Слайд 14
- 15. Гостиница «Прибалтийская»Казанский собор
- 16. Центральная симметрия в зоологии:
- 17. ЛягушкаПаукБабочка
- 18. инфузория-туфелька и амёба
- 19. Центральная симметрия в транспорте:
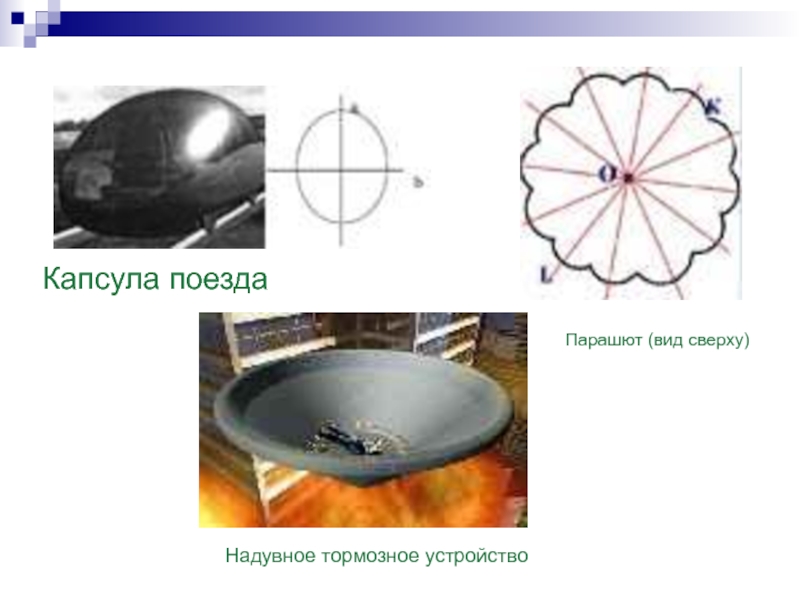
- 20. Надувное тормозное устройствоКапсула поездаПарашют (вид сверху)
- 21. А также с симметрией мы часто
- 22. Спасибо за просмотр!
- 23. Скачать презентанцию
Центральная симметрия. Определение: Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О
Слайды и текст этой презентации
Слайд 1Выполнил ученик: 8 класса
Рогожин Данила
Проверила: Муравьёва Валентина Владимировна
Центральная
симметрия.
Слайд 2 Центральная симметрия.
Определение:
Фигура называется симметричной
относительно точки О, если для каждой точки фигуры симметричная ей
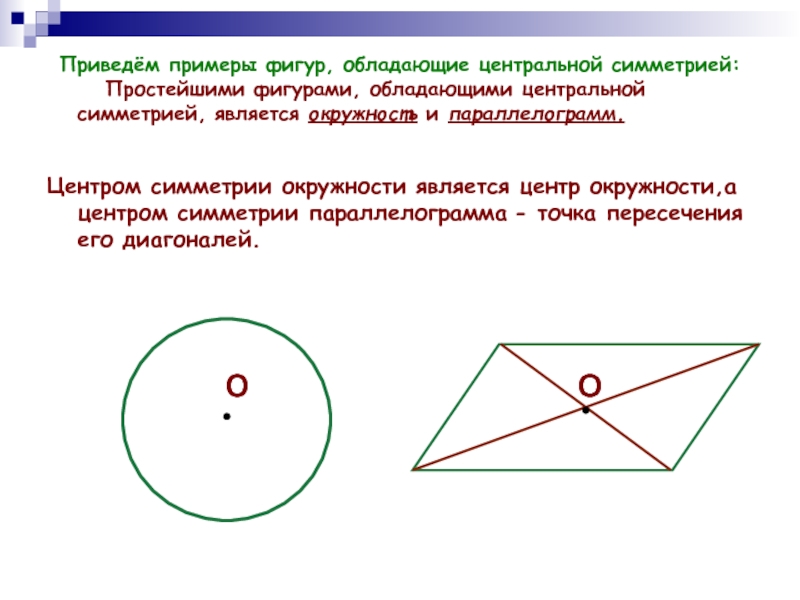
точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.Слайд 3 Приведём примеры фигур, обладающие центральной симметрией: Простейшими
фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
Центром симметрии окружности
является центр окружности,а центром симметрии параллелограмма - точка пересечения его диагоналей.
O
O
Слайд 4А
В
О
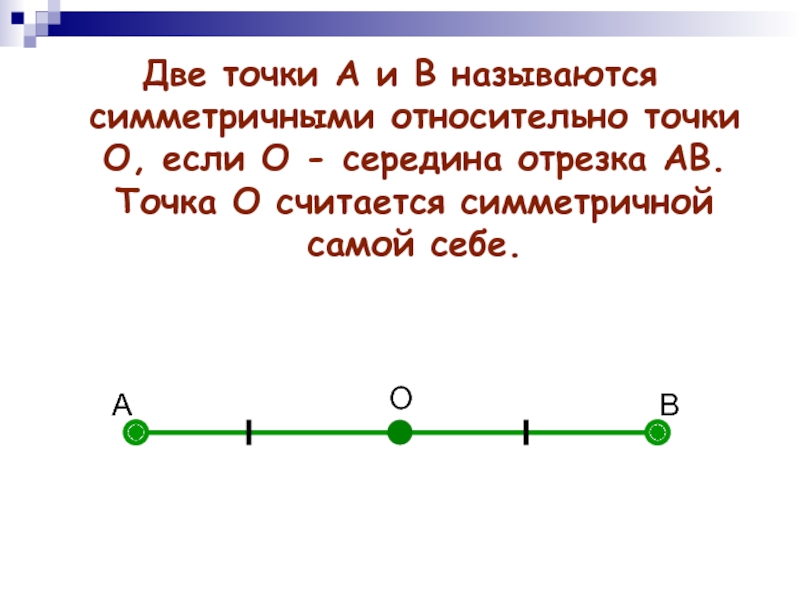
Две точки А и В называются симметричными относительно точки О,
если О - середина отрезка АВ. Точка О считается симметричной
самой себе.Слайд 5 Например:
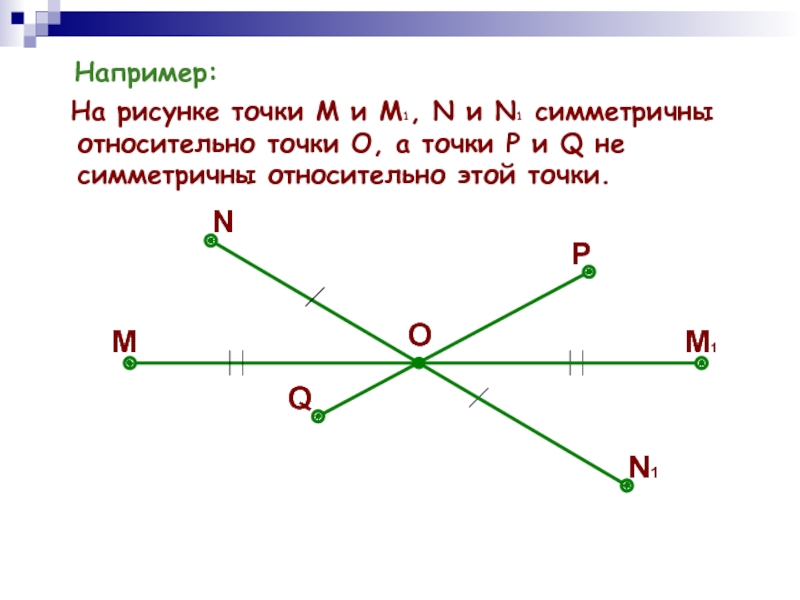
На рисунке точки М и М1, N и
N1 симметричны относительно точки О, а точки Р и Q
не симметричны относительно этой точки.М
М1
N
N1
О
Р
Q
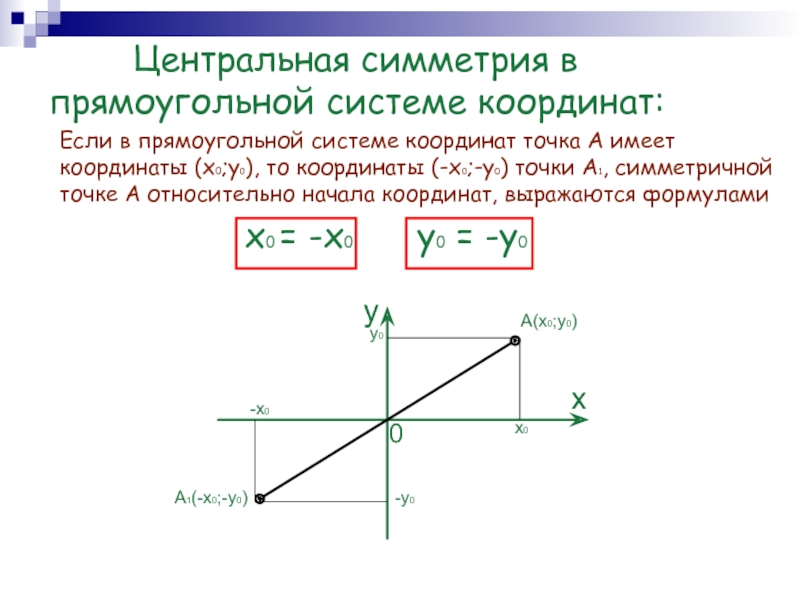
Слайд 6 Центральная симметрия в прямоугольной системе координат:
Если в прямоугольной системе координат точка А имеет
координаты (x0;y0), то координаты (-x0;-y0) точки А1, симметричной точке А относительно начала координат, выражаются формуламиx0 = -x0 y0 = -y0
у
х
0
А(x0;y0)
А1(-x0;-y0)
x0
-x0
y0
-y0
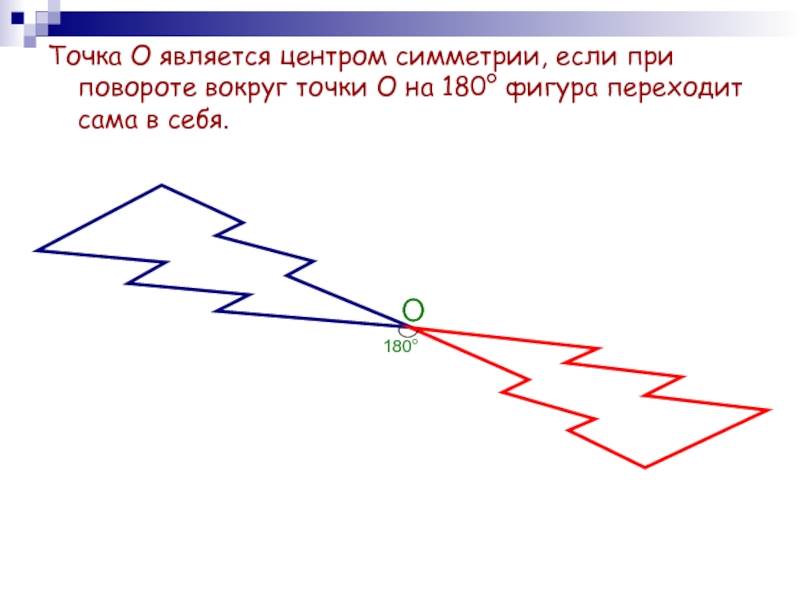
Слайд 11Точка О является центром симметрии, если при повороте вокруг точки
О на 180° фигура переходит сама в себя.
О
180°
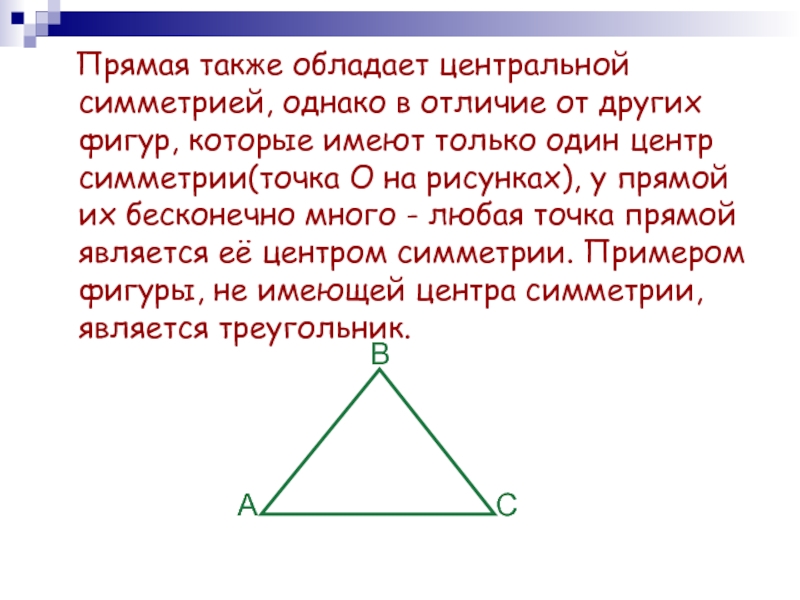
Слайд 12 Прямая также обладает центральной симметрией, однако в отличие
от других фигур, которые имеют только один центр симметрии(точка О
на рисунках), у прямой их бесконечно много - любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является треугольник.А
В
С
Слайд 13 Применение на практике:
Примеры симметрии в растениях:
Вопрос о
симметрии в растениях возник ещё в 5 веке до н. э. На явление симметрии в живой природе обратили внимание в Древней Греции пифагорейцы в связи с развитием ими учения о гармонии. В 19 веке появлялись отдельные работы, касающиеся этой темы. А в 1961 году как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика. Центральная симметрия характерна для различных плодов: голубика, черника, вишня, клюква. Рассмотрим разрез любой из этих ягод. В разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии. Центральную симметрию можно наблюдать на изображении таких цветов как цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки, а в некоторых случаях центральной симметрией обладает и изображение всего цветка ромашки. Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. Весь же цветок обладает центральной симметрией только в случае четного количества лепестков
Слайд 16Центральная симметрия в зоологии:
Рассмотрим,
как связаны животный мир и симметрия.
Центральная
симметрия наиболее характерна для животных, ведущих подводный образ жизни.А также есть пример асимметричных животных: инфузория-туфелька и амёба
Выводы:
Симметрию живого существа определяет направление его движения. Для живых существ, для которых ведущим направлением является направление движения “вперед”, наиболее характерна осевая симметрия. Так как в этом направлении животные устремляются за пищей и в этом же спасаются от преследователей. А нарушение симметрии привело бы к торможению одной из сторон и превращению поступательного движения в круговое.
Центральная симметрия чаще встречается в форме животных, обитающих под водой.
Асимметрию можно наблюдать на примере простейших животных.
Слайд 19Центральная симметрия в транспорте:
Центральная симметрия не
совместима с формой наземного и подземного транспорта. Причиной этого служит
его направление движения. При рассмотрении вида сверху трамвая, электровоза, телеги, мы видим, что ось симметрии проходит вдоль направления движения. Таким образом, центральную симметрию следует искать в воздушном и подводном транспорте, т. е. в таких видах, где направления: вперед, назад, вправо, влево, – равноценны.Один из таких видов транспорта – это воздушный шар.
Другой пример воздушного транспорта – это парашют. Ученые относят его изобретение еще к 13 веку. На нашем чертеже мы представили вид сверху воздушного шара. Отметим, что он аналогичен виду сверху парашюта. Как мы видим, эта фигура центрально симметрична. О – центр симметрии.
Слайд 21
А также с симметрией мы часто встречаемся в искусстве,
архитектуре, технике, быту. В большинстве случаев симметричны относительно центра узоры
на коврах, тканях, комнатных обоях.Симметричны многие детали механизмов, например зубчатые колёса.