Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цилиндр
Содержание
- 1. Цилиндр
- 2. ЦЕЛИ УРОКА:Ввести понятие цилиндрической поверхности , цилиндра
- 3. ЗАДАЧИ: 1. Изучить определение цилиндра, основные
- 4. В окружающем мире имеются предметы, имеющие форму цилиндра.
- 5. Слайд 5
- 6. Если в одной из 2 параллельных плоскостей
- 7. Слайд 7
- 8. Цилиндр – геометрическое тело. Радиусом цилиндра
- 9. ЦИЛИНДР.Цилиндр- геометрическое тело, ограниченное цилиндрической поверхностью (называемой
- 10. Слайд 10
- 11. Развертка боковой поверхности цилиндра.Представим себе, что боковую
- 12. S=пR²S=пR²hC=2пRАВАВА1В1
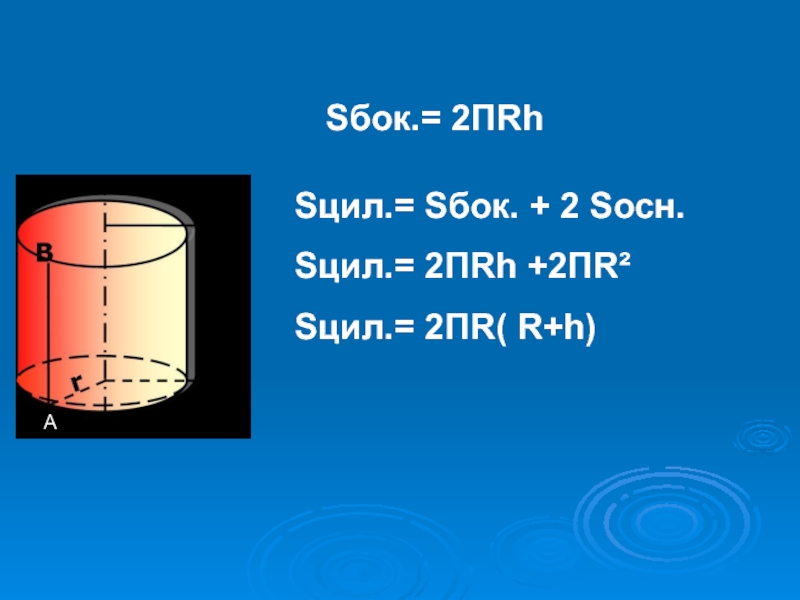
- 13. АSбок.= 2ПRhSцил.= Sбок. + 2 Sосн.Sцил.= 2ПRh +2ПR²Sцил.= 2ПR( R+h)
- 14. Задача.Сколько квадратных метров листовой жести пойдет на
- 15. Решение.Высота цилиндра 4м , диаметр основания 20
- 16. 1.Дайте определение цилиндра и его основных элементов.2.Чему
- 17. У С П Е Х О В !!!
- 18. Скачать презентанцию
ЦЕЛИ УРОКА:Ввести понятие цилиндрической поверхности , цилиндра и его элементов.Вывести формулы для вычисления площадей боковой и полной поверхностей цилиндра.Развивать самостоятельность учащихся в работе над задачами.
Слайды и текст этой презентации
Слайд 2ЦЕЛИ УРОКА:
Ввести понятие цилиндрической поверхности , цилиндра и его элементов.
Вывести
формулы для вычисления площадей боковой и полной поверхностей цилиндра.
Развивать самостоятельность
учащихся в работе над задачами.Слайд 3ЗАДАЧИ:
1. Изучить определение цилиндра, основные свойства цилиндра,
формулы для нахождения площади боковой поверхности, площади полной поверхности цилиндра.
2.
Научиться вычислять площадь поверхности цилиндра для решения практических задач.Слайд 6Если в одной из 2 параллельных плоскостей взять окружность, и
из каждой ее точки восстановить перпендикуляр до пересечения со второй
плоскостью, то получится тело, ограниченное двумя кругами и поверхностью образованной из перпендикуляров, которая называется цилиндрической, а сами перпендикуляры – образующими цилиндрической поверхности. Тело называется цилиндром. Круги называются основаниями цилиндра, отрезки образующих, заключенные между основаниями- образующими цилиндра.Слайд 7
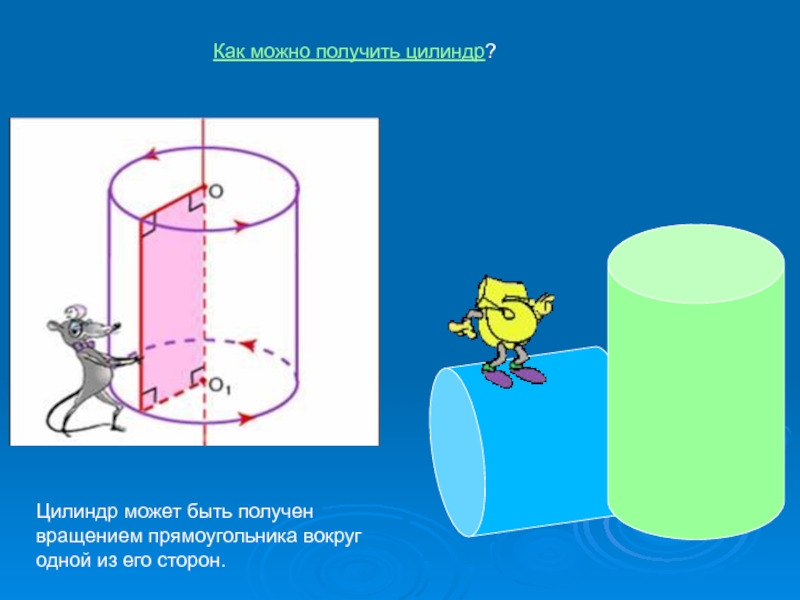
Как можно получить цилиндр?
Цилиндр может быть получен вращением
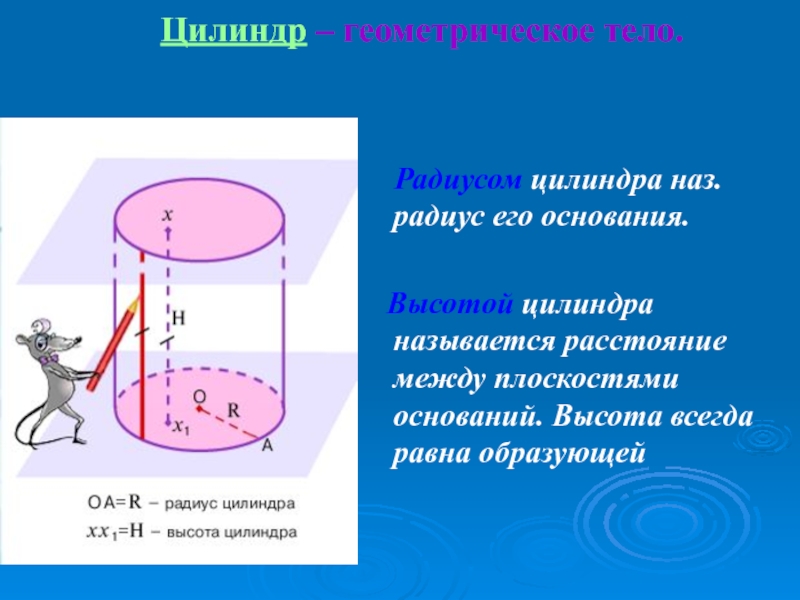
прямоугольника вокруг одной из его сторон.Слайд 8 Цилиндр – геометрическое тело.
Радиусом цилиндра наз. радиус его
основания.
Высотой цилиндра называется расстояние между плоскостями оснований. Высота
всегда равна образующейСлайд 9ЦИЛИНДР.
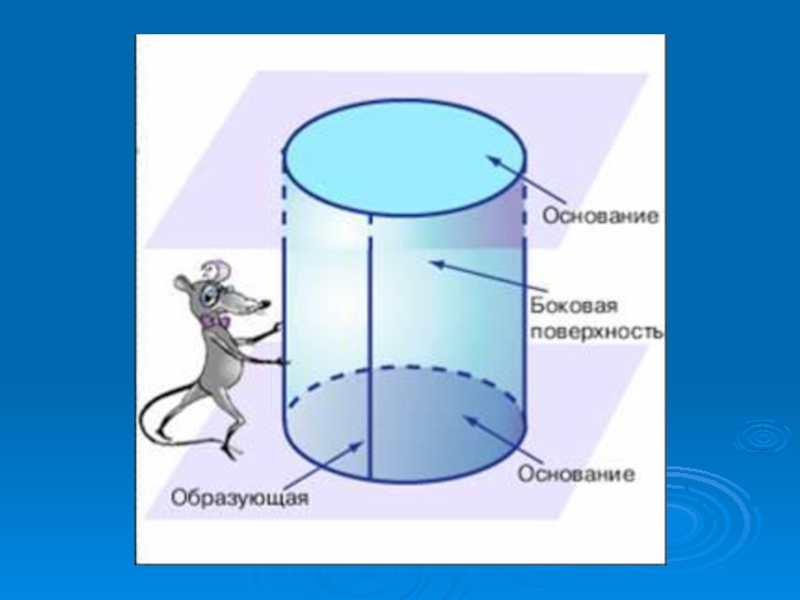
Цилиндр- геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра)
и не более чем двумя поверхностями
( основаниями цилиндра) ;
одно получено из другого параллельным переносом вдоль образующей боковой поверхности цилиндра.Слайд 11Развертка боковой поверхности цилиндра.
Представим себе, что боковую поверхность цилиндра разрезали
по образующей АВ и развернули таким образом, что получился прямоугольник
АВВ1А1. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Сторона АА1 прямоугольника является разверткой окружности основания цилиндра, а сторона АВ- образующей цилиндра.Слайд 12S=пR²
S=пR²
h
C=2пR
А
В
А
В
А1
В1
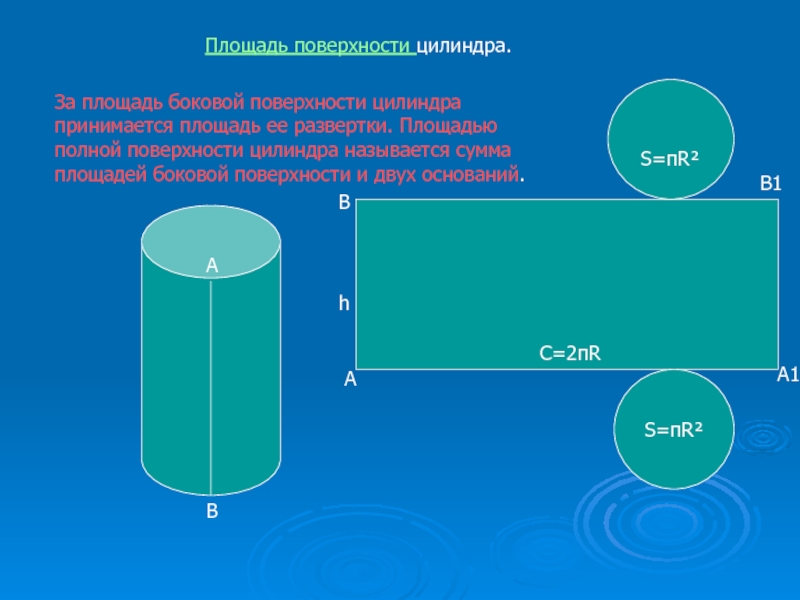
Площадь
поверхности цилиндра.
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.Слайд 14Задача.
Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной
4 м и диаметром 20 см. , если на швы
необходимо добавить 2,5 % площади ее боковой поверхности?Слайд 15Решение.
Высота цилиндра 4м , диаметр основания 20 см. = 0,2
м
S бок. = 2ПRh , R= 0,2: 2=0,1
м.Sбок.= 2П•0,1•4 =0,8П (м²)
Найдем 2,5% от 0,8П
2,5%=0,025
0,8П •0,025= 0,02П
0,8П+0,02П= 0,82П (м²)
П≈3,14
0,82•3,14≈2,5748 (м²)
Понадобится приблизительно 2, 58 м² листовой жести.
Слайд 16
1.Дайте определение цилиндра и его основных элементов.
2.Чему равна площадь боковой
поверхности цилиндра?
3.Чему равна площадь полной поверхности цилиндра?
Домашнее задание:
Задача.
Сколько
понадобится краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3м. , если на один квадратный метр расходуется 200 г краски?в о п р о с ы.