Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок-презентация по алгебре "Решение квадратных уравнений"
Содержание
- 1. Урок-презентация по алгебре "Решение квадратных уравнений"
- 2. Подумай!
- 3. Не торопись!
- 4. Слайд 4
- 5. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ.СПОСОБЫ РЕШЕНИЙ.
- 6. Задачи урока.1.Обобщить изученные способы решения квадратных
- 7. КВАДРАТНОЕ УРАВНЕНИЕ-ЭТО ОСНОВА ,ФУНДАМЕНТ ,НА КОТОРОМ ПОКОИТСЯ ВЕЛИЧЕСТВЕННОЕ ЗДАНИЕ АЛГЕБРЫ. .КВАДРАТНЫЕ УРАВНЕНИЯТРИГОНОМЕТРИЧЕСКИЕПОКАЗАТЕЛЬНЫЕЛОГАРИФМИЧЕСКИЕИРРАЦИОНАЛЬНЫЕ
- 8. РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ПО ФОРМУЛЕ.РЕШЕНИЕ УРАВНЕНИЙ С
- 9. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ. ах² +вх+с=0,а=0.
- 10. D>0,- 2 КОРНЯ. D=0,-1 КОРЕНЬ. D
- 11. РЕШИМ УРАВНЕНИЯ4х² +7х+3=0
- 12. Проверь себя:а)верно б) подумай
- 13. Решение уравнений с использованием т.Виета.х²+рх+q=0 -приведённое квадратное
- 14. По коэффициентам р и q можно предсказать
- 15. Если q < 0,то уравнение имеет два
- 16. Задание Не решая уравнения, определите знаки его
- 17. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ СПОСОБОМ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ.
- 18. Разложите на множители (самостоятельная работа)
- 19. Метод выделения полного квадрата. Уравнение х²+6х-7=0 решим
- 20. Графическое решение квадратного уравнения.Приведённое квадратное уравнение :х²+рх+q=0
- 21. Решим графически уравнение: 4х²-12х-8=0Разделим обе части уравнения
- 22. Решим графически уравнение :
- 23. 1111111093yx
- 24. Квадратичная функция. Решая квадратное уравнение, мы
- 25. Определить нули функции, если они есть: у
- 26. Определись в своих знаниях и проверь свои
- 27. Верные варианты ответов:1)-12)-53)-64)-25)-4
- 28. Заключение.Знание способов решения квадратных уравнений и умение
- 29. Всем Учащимся 9 класса игостям, присутствующим на нашем уроке,выражаем большую БЛАГОДАРНОСТЬ.
- 30. Слайд 30
- 31. Конец.
- 32. Скачать презентанцию
Подумай!
Слайды и текст этой презентации
Слайд 6 Задачи урока.
1.Обобщить изученные способы решения квадратных уравнений.
2.Систематизировать знания учащихся
в умении решать квадратные уравнения разными способами.
информатизации и осуществить самоконтроль.
Слайд 7КВАДРАТНОЕ УРАВНЕНИЕ-ЭТО ОСНОВА ,ФУНДАМЕНТ ,НА КОТОРОМ ПОКОИТСЯ ВЕЛИЧЕСТВЕННОЕ ЗДАНИЕ АЛГЕБРЫ.
.
КВАДРАТНЫЕ
УРАВНЕНИЯ
ТРИГОНОМЕТРИЧЕСКИЕ
ПОКАЗАТЕЛЬНЫЕ
ЛОГАРИФМИЧЕСКИЕ
ИРРАЦИОНАЛЬНЫЕ
Слайд 8РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ПО ФОРМУЛЕ.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ Т.ВИЕТА.
РАЗЛОЖЕНИЕ КВАДРАТНОГО
УРАВНЕНИЯ НА МНОЖИТЕЛИ.
МЕТОД ВЫДЕЛЕНИЯ ПОЛНОГО КВАДРАТА.
ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ.
НЕКОТОРЫЕ СПОСОБЫ
Слайд 9РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ.
ах² +вх+с=0,а=0. УМНОЖИМ ОБЕ
²
ЧАСТИ НА 4а
И ИМЕЕМ: 4а² х² +4авх+4ас=0 ((2ах) ² +2ах2в+в² )-в² +4ас=0 (2ах+в)
² = в² -4ас 2ах+в=±√в² -4ас 2ах=-в±√в² -4ас х1,2 = -в±√в² -4ас 2а в² -4ас=D.
0,- 2 КОРНЯ. D=0,-1 КОРЕНЬ. D" alt="D>0,- 2 КОРНЯ. D=0,-1 КОРЕНЬ. D">Слайд 11РЕШИМ УРАВНЕНИЯ
4х² +7х+3=0
4х ²+ 20х+25=0
Х ² -6х-40=0
Выбери верный ответ:
-3/4; -1
1; 3/4
4; 3
0; 5
8; 5
5,6
Корней
Нет
-2,5;
-4; 10
Слайд 12Проверь себя:
а)верно б) подумай в)торопишься
а)НЕ СПЕШИ б)верно
в)проверь
а) ПОДУМАЙ б)ПРОВЕРЬ
в)верно
Слайд 13Решение уравнений с использованием т.Виета.
х²+рх+q=0 -приведённое квадратное уравнение.
Его корни
удовлетворяют т.Виета, которые при а=1, имеет вид
х1х2=q,х1+х2=-р.
}
Слайд 14По коэффициентам р и q можно предсказать знаки корней.
Если q>0,то
уравнение имеет два одинаковых по знаку корня и это зависит
ОТ КОЭФФИЦИЕНТА P.ЕСЛИ Р > 0, ТО ОБА КОРНЯ ОТРИЦАТЕЛЬНЫ.
Х²+8Х+7=0,Т.К.Р=8,q=7, ТО
Х1=-7,Х2=-1.
ЕСЛИ Р < 0, ТО –ПОЛОЖИТЕЛЬНЫ
Х²-3Х+2=0, Т.К. Р=-3,q=2, ТО
Х1=1;Х2=2
0,то уравнение" alt="По коэффициентам р и q можно предсказать знаки корней.Если q>0,то уравнение имеет два одинаковых по знаку корня">Слайд 15Если q < 0,то уравнение имеет два разных по знаку
корня, причём больший по модулю корень имеет положительный знак,
если Р<0 , х²-8х-9=0,т.к. р=-8,q=-9,то х1=9,х2=-1. и отрицательный знак, если Р > 0. х²+4х-5=0,т.к. р=4,q=-5,то х1=-5, х2=1
Слайд 16Задание
Не решая уравнения, определите знаки его корней.
х ²-2х -15=0
х
²+2х-8=0
х ² -12х+35=0
3х ²+14х+16=0
х ²-5х+6=0
х ²-2х+1=0
(+;-) (5;-3)
(+;-) (-4;2)
(+;+) (5;7)
(-;-)
(+;+) (2;3)
(+;+) (1)
Слайд 17РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ СПОСОБОМ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ.
КВАДРАТНОЕ УРАВНЕНИЕ ах²+вх+с=0
РАЗЛОЖИМ НА МНОЖИТЕЛИ по ФОРМУЛЕ а(Х-Х1 )(Х-Х2)=0,где х1 и х2-корни
уравнения.
а) х ² +10х-24=0
х² +12х-2х-24=(х² +12х)-(2х+24)=
х(х+12)-2(х+12)=(х+12)(х-2)=0
х1=-12; х2=2.
б) 6х² +х-2=0
6х² +х-2=6х² +4х-3х-2=3х(2х-1)+2(2х-1)=
(3х+2)(2х-1)=0
х1=-2/3; х2=1/2.
Слайд 18Разложите на множители (самостоятельная работа) 4х²+7х-2=0
х²-4х+4=0 х²+2х-8=0
х²+4х+4=0 х²-3х=0 6х²-7х+2=0 х²-81=0 х²-3х+2=0
Слайд 19Метод выделения полного квадрата. Уравнение х²+6х-7=0 решим , выделив полный квадрат х²+6х-7=х²+2*3*х+ 3²
-3²-7= (х+3) ²-16=0 т.е.(х+3) ²=16 х+3=4 или х+3=-4 х=1
х=-7
Слайд 20Графическое решение квадратного уравнения.
Приведённое квадратное уравнение :х²+рх+q=0
1.Перепишем его так:
х²= -рх-q
2.Построим графики зависимостей: у= х²;
у= -рх-q.График первой зависимости –парабола.
График второй зависимости -прямая.
Найдём точки пересечения параболы и прямой.
Абсциссы точек пересечения являются корнями квадратного уравнения.
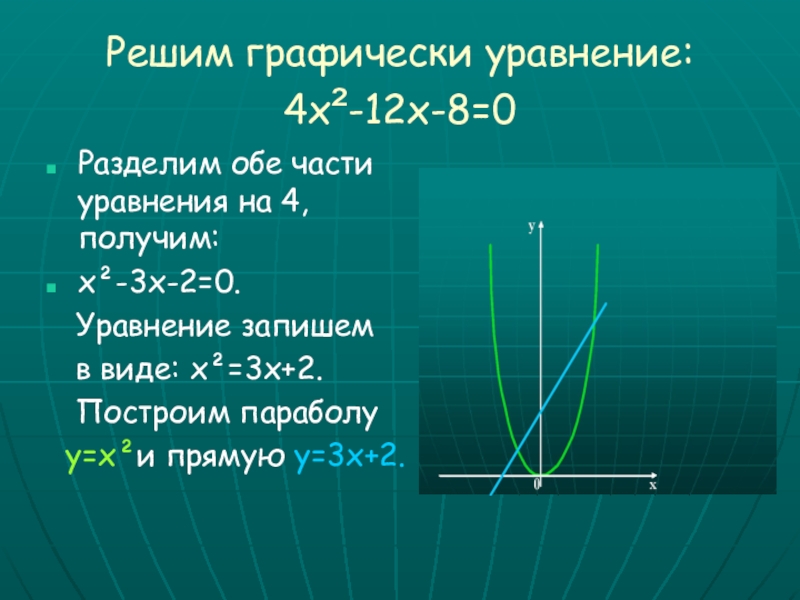
Слайд 21Решим графически уравнение:
4х²-12х-8=0
Разделим обе части уравнения на 4, получим:
х²-3х-2=0.
Уравнение запишем
в виде: х²=3х+2.
Построим параболу
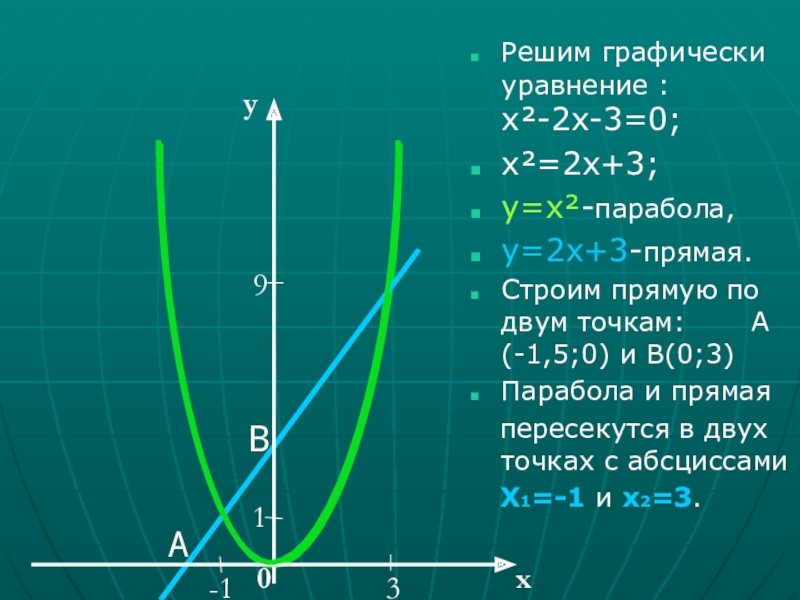
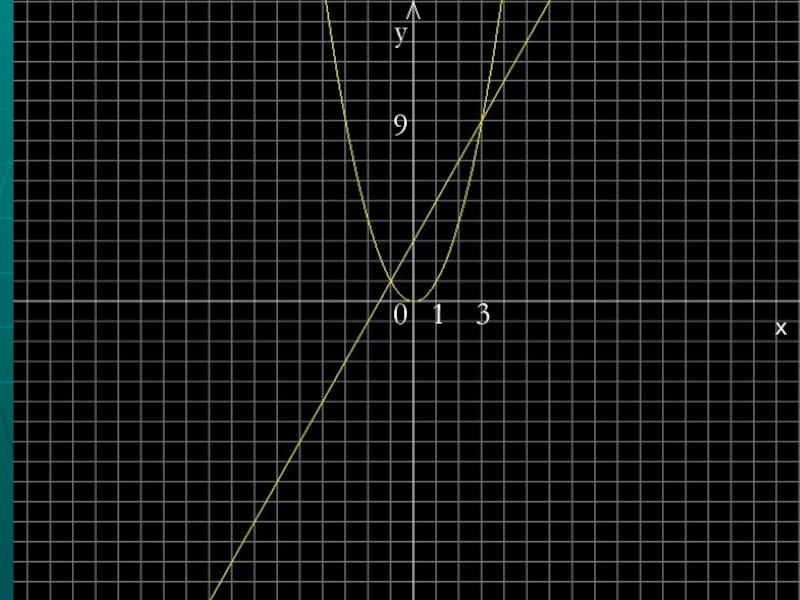
у=х²и прямую у=3х+2.
Слайд 22Решим графически уравнение :
х²-2х-3=0;
х²=2х+3;
у=х²-парабола,
у=2х+3-прямая.
Строим прямую по двум точкам:
А(-1,5;0) и В(0;3)Парабола и прямая
пересекутся в двух точках с абсциссами
Х1=-1 и х2=3.
Слайд 24 Квадратичная функция. Решая квадратное уравнение, мы находим нули функции, т.е.квадратичную функцию приравниваем 0
и решаем уравнение f(х)=0. Действительные, корни этого уравнения являются нулями функции
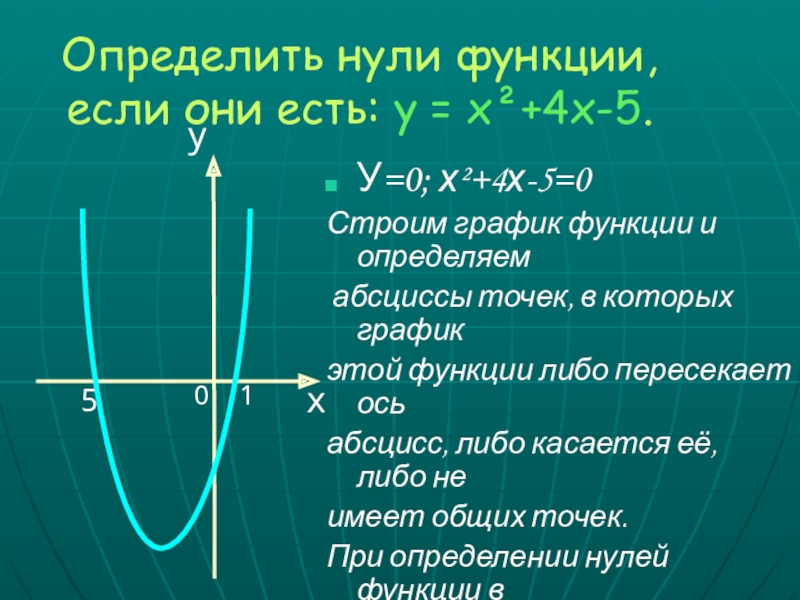
у=f(х).
Слайд 25Определить нули функции,
если они есть: у = х²+4х-5.
У=0; х²+4х-5=0
Строим график
функции и определяем
абсциссы точек, в которых график
этой функции
либо пересекает ось абсцисс, либо касается её, либо не
имеет общих точек.
При определении нулей функции в
первую очередь определяем знак Д и
знак коэффициента а .
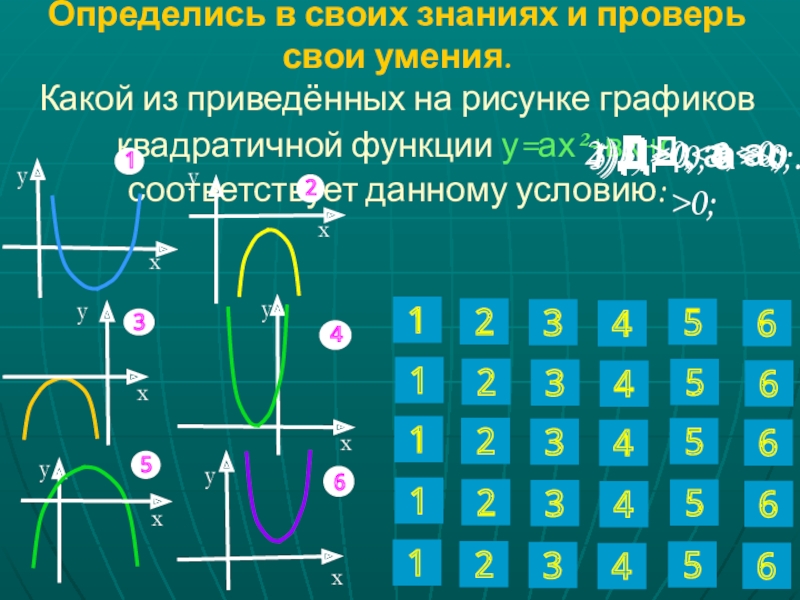
Слайд 26Определись в своих знаниях и проверь свои умения. Какой из приведённых
на рисунке графиков квадратичной функции у=ах²+вх+с соответствует данному условию:
1
2
6
5
4
3
1
2
6
5
4
3
1
2
6
5
4
3
1
2
6
5
4
3
1) Д>0,
а >0;2) Д>0, а<0;
1
2
6
5
4
3
3) Д <0, а >0;
4) Д<0, а< 0;
5) Д= 0, а >0 .
Слайд 28Заключение.
Знание способов решения квадратных уравнений и умение работать с графиками
поможет нам в дальнейшем при решении неравенств второй степени с
одной переменной и решении систем квадратных уравнений.
Слайд 29Всем
Учащимся 9 класса
и
гостям, присутствующим на
нашем уроке,
выражаем
большую
БЛАГОДАРНОСТЬ.
